163. feladványunkban Sherlock Holmes és Dr. Watson szeretnék Moriarty professzor telefonját feltörni. A telefont egy négyjegyű PIN-kód védi, amiről azt tudjuk, hogy az egymást követő számjegyek egymással szomszédosak a billentyűzeten (lásd az ábrát), megengedve az átlós lépést is, de nem megengedve a helyben maradást. Ha három másodperc alatt tudnak kipróbálni egy kombinációt, akkor mennyi ideig tart az összes lehetséges kombináció kipróbálása?

A legkevesebb szomszédja az 1-es, 3-as és 0-ás billentyűknek van, számszerűen három; négy szomszédja van a 7-es és 9-es billentyűknek; öt szomszédja a 2-es, 4-es és 6-os billentyűknek; hat szomszédja a 8-as billenytűnek; és a maximális nyolc darab szomszédja van az 5-ös billentyűnek. Bármelyik számjeggyel kezdhetünk a 10 közül, ezért az összes lehetséges kombináció valahol 10×3×3×3 = 270 és 10×8×8×8 = 5120 között lesz. Ha azt vesszük, hogy a szomszédok átlagos száma (3×3+2×4+3×5+1×6+1×8)/10 = 4,6, akkor úgy becsülhetjük, hogy a lehetséges kombinációk száma nagyjából 10×(4,6^3) ≈ 973. Ha viszont pontosan le akarjuk számolni, akkor nehezebb dolgunk van. Számítógéppel természetesen könnyű végigvenni az összes lehetőséget, de papíron kicsit nehézkesebb végigszámolni.

Rajzoljunk egy fatörzset, amit tízfelé ágaztatunk az első szinten. Az első szinten minden ág egy billentyűnek felel meg: a PIN-kód első számjegyének. Ezután az 1-es ágat, ami az első számjegynek felel meg, háromfelé ágaztatjuk, mert három lehetséges folytatás lehetséges az 1-es billentyűtől. A 2-es ágat ötfelé ágaztatjuk, mert öt lehetséges folytatás lehetséges a 2-es billentyűtől, és így tovább. Így kapjuk a második szinten lévő ágakat, szám szerint 46 darabot. Ha ez megvan, akkor a kapott ágak mindegyikét tovább ágaztatjuk a harmadik szinten, majd még egyszer a negyedik szinten, és végül megszámoljuk, hogy hány ág van összesen a negyedik szinten.

Papíron a második szintet még könnyen le tudjuk rajzolni, de a harmadik és negyedik szinthez már jó nagy papír kéne. Lehet azonban alkalmazni egy kis trükköt. A második szinten lévő 46 esetet kategorizálhatjuk aszerint, hogy éppen melyik billentyűnél járunk, azaz mi a PIN-kód második számjegye. Több olyan ág is lesz a második szinten, amikre a második számjegy ugyanaz, és ezekre a lehetséges folytatások száma ugyanaz lesz, azaz nem kell minden ágra külön végigszámolni, elegendő csak a tíz lehetséges számjegyre. Példaként a 2-es billentyűtől indulva a lehetséges folytatások ezek: 12, 14, 15, 32, 35, 36, 41, 42, 45, 47, 48, 51, 52, 53, 54, 56, 57, 58, 59, 62, 63, 65, 68, 69. De minket igazából ezeknek csak a száma érdekel, ami nem más, mint a 2-es billentyű szomszédjaira összeadva azok szomszédjainak számát: 3+3+5+8+5 = 24 lehetőség összesen. Ezt a 24 lehetőséget tehát elég egyszer összeszámolnunk, nem kell ötször megismételni.

A fentiekben lényegében azt csináltuk, hogy két részre bontottuk a PIN-kódot, az első kettő és az utolsó kettő számjegyre, és így egyszerűsítjük le a számlálást. Ezt azért tehetjük meg, mert az alapfeladat szerint a PIN-kód vissza is kanyarodhat, tehát a folytatást nem befolyásolja a PIN-kód eleje, vagyis függetlenül számlálhatjuk le a két rész lehetséges eseteinek a számát. Továbbá a számok elrendezésének tengelyes szimmetriáját is ki lehet még használni némi egyszerűsítésre, eszerint például az első szintről induló 1-es ág és a hozzá tartozó lombkorona pont ugyanakkora lesz, mint az első szintről induló 3-as ág és az ahhoz tartozó lombkorona. Hasonlóan a 4-es és a 6-os is egyezni fog egymással, továbbá a 7-es és 9-es is.

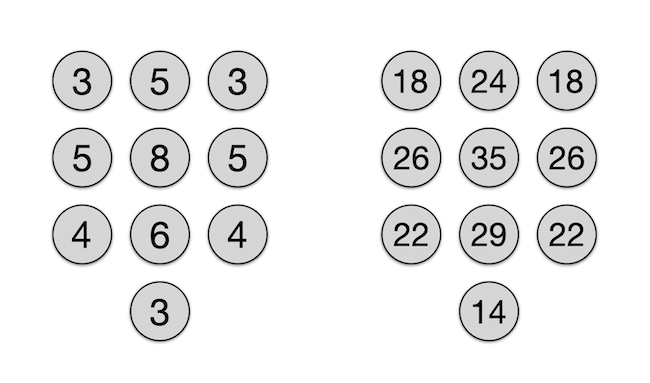
Az alábbi ábra bal oldalán az egyes billentyűk helyére a szomszédjaik számát írtuk bele, amiket a legelején már felsoroltunk, míg a jobb oldalon a szomszédjaik szomszédjainak összegét. Ezek segítségével a végeredmény már könnyen kiszámolható: egyszerűen össze kell szorozni a bal oldali számokat páronként a jobb oldali számokkal, és összeadni őket: 3×18 + 5×24 + 3×18 + 5×26 + 8×35 + 5×26 + 4×22 + 6×29 + 4×22 + 3×14 = 1160, ami 3480 másodpercnek felel meg, vagyis pont 58 percnek, azaz egy órán belül fel tudják törni a telefont.