Ész Ventura: Mennyire befolyásolhatja egy futballbíró a jövőt?
Egy olvasónk hívta fel rá a figyelmet, hogy furcsa eset történt a legutóbbi labdarúgó-világbajnokság negyeddöntőjében. A Marokkó–Portugália mérkőzést egy argentin játékvezető vezette, miközben Argentína még versenyben volt, ezért az esélyeiket befolyásolhatta, hogy gyengébb vagy erősebb csapat jut-e tovább a másik ágon. Hogy mennyire befolyásolhatta? Erről szólt 170. feladványunk.
Feladványunkban feltettük, hogy minden csapatnak van egy fix erőssége, és ha ez két csapat esetében A és B, akkor a továbbjutási esélyük A:B. A feladat fő kérdése az volt, hogy abban az esetben, ha az argentinok a döntőbe jutnak (ma már tudjuk, hogy ez megtörtént), igaz-e, hogy annál jobban járnak, minél gyengébb a Marokkó–Portugália mérkőzés győztese, vagyis elvben érdemes-e az argentín bírónak a gyengébbik csapat továbbjutását segítenie?
Az argentinok egyébként a hollandokat verték a negyeddöntőben, majd a horvátokkal kerültek össze az elődöntőben. Minket azonban most nem érdekelnek ezek a csapatok és erősségeik, hiszen a feladat kérdése arra az esetre vonatkozott, hogy mi van akkor, ha az argentinok a döntőbe jutnak, és lényegtelen volt az, hogy hogyan. Ami jobban érdekel minket, az a másik ág és az ott lévő csapatok erőssége, hiszen azokból a csapatokból került ki Argentína potenciális ellenfele a döntőben.
A másik ágon a Marokkó–Portugália mérkőzés győztese az Anglia–Franciaország mérkőzés győztesével került össze, ranglista alapján azonban az argentinok, az angolok és a franciák erőssége nagyjából egyforma (A), ezt tételeztük fel a feladatban is. Szintén a fenti ranglista szerint Portugália gyengébb (B), Marokkó pedig jelentősen gyengébb (C); ők történelmet is írtak, hiszen ők lettek az első afrikai csapat, amely a legjobb négy közé jutott egy világbajnokságon.
A feladat tehát feltételes valószínűségek kiszámolására irányult. Meg kell nézni azt az esetet, amikor Marokkó jut tovább, és azt, amikor Portugália, de mindkét esetben két eset van még arra vonatkozóan, hogy ki jut a döntőbe ezen az ágon. Nézzük meg, mik az esélyek!
Portugália továbbjutása esetén B/(A+B) annak a valószínűsége, hogy Portugália a döntőig jut, és A/(A+B) a valószínűsége annak, hogy egy argentinokkal azonos erősségű csapat jut a döntőbe (angolok vagy franciák). Marokkó esetében C/(A+C) annak a valószínűsége, hogy Marokkó a döntőig jut, és A/(A+C) a valószínűsége annak, hogy egy argentinokkal azonos erősségű csapat jut a döntőbe.
Ha az argentinok döntőt játszanak, akkor azt az alábbi esélyekkel nyerik meg. Ha az ellenfelük velük azonos erősségű csapat, akkor 1/2 eséllyel nyernek, ha Portugáliával játszanak, akkor A/(A+B) az esélyük a győzelemre, ha Marokkóval, akkor pedig A/(A+C). Természetesen az lenne jobb nekik, ha Marokkóval kerülnének össze, és ezért tűnik úgy elsőre, hogy jobb lenne nekik, ha Marokkó nyerné a Marokkó–Portugália mérkőzést. Igen ám, de ha a gyengébbik csapat jut tovább, akkor az elődöntőben könnyebben megverik, és ezért növekszik annak a valószínűsége, hogy az argentinok mégis egy erősebb csapatot kapnak a döntőben. A két hatás egymás ellen dolgozik.
Nézzük a teljes nyerési esélyt a két esetre. Ha Portugália jut tovább, akkor [B/(A+B)]·[A/(A+B)] + [A/(A+B)]·[1/2] Argentína világbajnoki esélye. Ha Marokkó jut tovább, akkor [C/(A+C)]·[A/(A+C)] + [A/(A+C)]·[1/2] Argentína világbajnoki esélye. Ha a nevezőket és a számlálókat is elosztjuk A-val, és bevezetjük a b = B/A és c = C/A jelöléseket, akkor most b vagy c helyett csak x-et írva, az a kérdés lényegében, hogy az alábbi függvény monoton-e a [0,1] intervallumon.
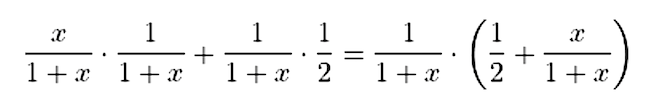
Az derül ki, hogy nem monoton. Ha ábrázoljuk ezt a függvényt 0 és 1 közötti x-ekre, akkor kiderül, hogy a függvénynek x = 1/3 -nál van maximuma. Egyébként a függvény 0-ban és 1-ben is 1/2 értéket vesz fel, ami annak az esetnek felel meg, amikor az adott csapat nagyon gyenge, vagy pedig A-val egyező erősségű. A maximum értéke továbbá 9/16, tehát a játékvezető maximum 1/16-dal tudja növelni az argentinok esélyét a világbajnoki győzelemre, de az csak akkor lehetséges, ha Marokkó elhanyagolhatóan gyenge és Portugália éppen harmadolyan erős, mint Franciaország, vagy akkor, ha Portugália közel ugyanolyan erős mint Franciaország, Marokkó pedig harmadannyira erős.
Kapcsolódó cikk a Qubiten:
