A 171. feladványban különböző módszereket írtam le arra, hogy miként lehet ajándékozás lebonyolítani egy iskolai osztályban. A legegyszerűbb az lenne, hogy bedobják a neveket egy kalapba, és mindenki véletlenszerűen húz egyet. Ezzel csak az a baj, ha valaki a saját nevét húzza (vagy akár többen is), akkor mindenkinek újra kell húzni. És ha másodszor is a saját nevét húzza valaki, akkor megint, és így tovább. Na de vajon mekkora annak az esélye, hogy nem kell újra húzni?

Ha tippelni kellene, a legtöbben valószínűleg azt mondanák, hogy egy nagy létszámú osztályban kicsi a valószínűsége annak, hogy szükség lesz újrahúzásra. Ha valaki jobban belegondol, és van érzéke a valószínűség-számításhoz vagy a kombinatorikához, lehet, hogy ezzel ellentéteset sejtene, mégpedig azt, hogy a létszám növelésével egyre nagyobb lesz az újrahúzás valószínűsége. Ezt a sejtést támasztaná alá, ha megnézné az ember, hogy mi a helyzet két vagy három fő esetén. Két főnél a kihúzás sorrendje kétféle lehet, az egyik jó, a másik rossz. Három főnél a kihúzás sorrendje 3! = 6 féle lehet, és ezekből négy esetben kellene újrahúzni, tehát 1/2-ről 2/3-ra nőtt az újrahúzás valószínűsége.

Ezek után igazán meglepő, hogy mégsem igaz, hogy az újrahúzás valószínűsége a létszámmal folyamatosan növekszik. Ha tovább nézzük, akkor azt találjuk, hogy négy főre 15/24, vagyis 62,5% az újrahúzás valószínűsége, ami csökkenés a 2/3-hoz képest. Tovább vizsgálódva kiderül, hogy ez a valószínűség a létszám egyesével történő növelése során oszcillálva fog egy se nem nulla, se nem 1 értékhez tartani, mégpedig konkrétan (1-1/e)-hez, ahol e az Euler-féle szám, azaz a természetes logaritmus alapszáma. Annak a valószínűsége tehát, hogy nem kell újrahúzni, az alábbi:

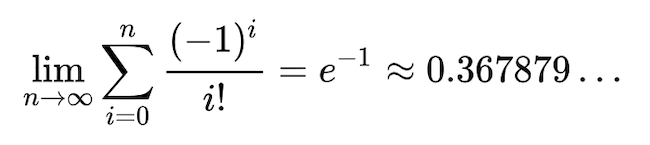
De hogy jön ide a természetes logaritmus alapszáma? N ember lehetséges sorbarendezéseinek száma N·(N-1)·(N-2)··· , amit N faktoriálisnak nevezünk és N!-al jelölünk. Az e értéke pedig N!-okat tartalmazó limeszként is előáll, így lehetséges az, hogy az Euler-féle szám belekerül egy ilyen képletbe (a levezetést és a bővebb magyarázatot lásd itt). A valószínűség-számításban sok érdekesség van, még a geometriából ismert pi (π) is meg tud jelenni valószínűség-számítási képletekben. Például annak a valószínűsége, hogy két véletlenszerűen választott egész szám relatív prímek legyenek, 6/π² ≈ 60,8%.

Na de nem kell megijedni, a feladványban nem kellett sem e-t, sem π-t tartalmazó képleteket számolni. A fenti húzási módszer továbbfejlesztésére több lehetőséget is ismertettünk. Ezeknek az volt a lényegük, hogy a lehetséges újrahúzások számát, azaz a húzási procedúra várható hosszát csökkentsük. A legutolsó módszer olyan volt, hogy garantálva legyen, hogy a legvégén nem kell semmilyen esetben újrakezdeni. Nézzük még egyszer, mi volt a húzási módszer ebben az utolsó esetben, amire a feladat vonatkozott.

Az algoritmus szerint minden gyerkőc felírta a nevét egy cetlire, majd a cetliket bedobták egy kalapba, továbbá az osztályfőnök nevét is bedobták még két példányban a többi név közé. Az osztályfőnök kezdte a húzást, és ha a saját nevét húzta ki, akkor újat húzott. Ha másodszor is a saját nevét húzta, akkor megint újat húzott, majd a saját neveit visszadobta a kalapba. Ezután egyesével húzott minden gyerek. Mindenki rögtön megnézte a cetlijét, és ha saját magát húzta, akkor húzott egy másikat, a saját nevét tartalmazó cetlit pedig visszadobta a kalapba. A legvégén az osztályfőnök húzott még egyet. Ha utoljára magát húzta, akkor ő csak egyvalakit ajándékozott meg, és neki is csak egy gyerek adott ajándékot. Ellenkező esetben viszont ketten ajándékozták meg, és ő is két gyereknek adott ajándékot.

A feladat kérdése az volt, hogy minden gyereknek ugyanakkora esélye van-e kihúznia az osztályfőnököt? Ha sorrendtől függetlenül azonosak lennének az esélyek, akkor ennek a bizonyítására valami általános számítást kéne adnunk. Sokkal könnyebb dolgunk lenne, ha az állítás nem lenne igaz, mert akkor elég lenne két gyereket mutatni, akik nem ugyanakkora valószínűséggel húzzák ki az osztályfőnököt. Érdemes tehát előbb csak az első és a második gyerekre kiszámolni a szóban forgó valószínűséget, hátha nem lesznek azonosak.

Az első gyerek esélyei

Az algoritmus szerint az osztályfőnök biztosan kihúzza egy gyerek nevét, és mivel ő az első, ezért mindenkit azonos, 1/30 eséllyel. Tehát 1/30 eséllyel húzza ki például azt a gyereket, aki utána fog húzni (jelöljük A-val), és 29/30 eséllyel valaki mást. Ha az osztályfőnök A-t húzza, akkor A a maradék 29 gyereknévből és az osztályfőnök két cetlijéből, azaz összesen 31 cetliből bármit húzhat, és 2/31 az esélye, hogy az osztályfőnököt fogja húzni.

Ha viszont az osztályfőnök nem A-t húzza, akkor mivel A nem húzhatja saját magát, ezért csak 28+2 = 30 névből kaphat valakit, és ilyenkor az osztályfőnök kihúzásának 2/30 az esélye. Összesítve tehát annak a valószínűsége, hogy A az osztályfőnököt húzza, az alábbi súlyozott átlag lesz: (1/30)·(2/31) + (29/30)·(2/30) ≈ 6,66%.

A második gyerek esélyei

A továbbiakban jelöljük az osztályfőnököt O-val, az utána húzó gyereket A-val, az utána következőt B-vel, és az összes többi gyerekre, aki se nem A és se nem B, használjuk a C jelölést. Most nézzük, hogy B mekkora valószínűséggel húzza ki O-t. Hasonló módon kell összegezni, ahogyan az előbb tettük, csak most attól függően, hogy az O és A kit húzott, kicsit több esetet kell átnézni. Az osztályfőnök tekintetében három eset lehetséges, vagy A-t húzza, vagy B-t, vagy valamelyik másik gyereket, akit C-vel jelölünk. Ezt a három esetet fogjuk most különválasztva részletesen megnézni.

Az osztályfőnök A-t húzza eset. Ennek a valószínűsége 1/30, és ekkor A-nak marad 31 cetli a kalapban, amiből húzhat (29 gyerek és kétszer az osztályfőnök). Annak a valószínűsége, hogy A kihúzza ezek után valamelyik osztályfőnöki cetlit 2/31, és ekkor B-nek már csak egy osztályfőnöki cetli marad, amit kihúzhat 29 cetli közül (mert magát nem húzhatja), tehát 1/29 valószínűséggel.

Ha A B-t húzza, amire 1/31 az esélye, akkor B-nek 30 cetli marad, amiből húzhat bármit, mert saját maga már nincs a kalapban, így 2/30 lesz annak a valószínűsége, hogy az osztályfőnököt húzza. Ha pedig 28/31 valószínűséggel A valaki mást húz (C), aki se nem A, se nem B, se nem az osztályfőnök, akkor ezek után B 2/29 eséllyel húzza az egyik osztályfőnöki cetlit.

Az osztályfőnök B-t húzza eset. Ennek a valószínűsége szintén 1/30. Ekkor A nem húzhatja magát, de B-t sem, mert őt már kihúzták, tehát csak két eset lehet, vagy 2/30 eséllyel O-t húz, vagy 28/30 eséllyel C-t húz. Az előbbi esetben B 1/30 eséllyel húzza ki a maradék O cetlit, a második esetben 2/30 valószínűséggel húzza ki valamelyik O cetlit a két bentmaradóból.

Az osztályfőnök se nem A-t, se nem B-t húz esete. Ennek a valószínűsége 2/30. Ekkor A 2/30 valószínűséggel húzhat O-t, 1/30 valószínűséggel B-t, és 27/30 eséllyel valaki mást, akit most jelöljünk C'-vel. Az első esetben B 1/29 eséllyel húzza ki a maradék O cetlit, a második esetben 2/30 eséllyel, a harmadik esetben pedig 2/29 eséllyel valamelyik O cetlit a két bentmaradóból.

Mindent összesítve az alábbi képlet adja annak a valószínűségét, hogy B O-t húz, és ez 6,65%, tehát nem azonos azzal, hogy A O-t húz!

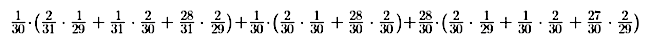
Kapcsolódó cikk a Qubiten: