A Typotex Kiadó A logika világa sorozatában megjelent Dr. Ecco talányos kalandjai című könyve igazán különleges fejtörőkötet, amiben Dennis E. Shasha úgy mutat be olvasmányos történetekben érdekfeszítő feladványokat, hogy azok tényleg a való élet különböző területeiről származó igazi problémák – többnyire optimalizációs feladatok –, amiket bárki könnyedén megérthet, a legtöbbjüket kis kitartással meg tudja oldani; igaz, helyet kapott a könyvben néhány nehéz probléma is, sőt olyannal is találkozhatunk, amely mindezidáig megoldatlan maradt. Csak hogy néhányat említsek a könyv által érintett területekből: sport, építőipar, közlekedésmérnökség, hadászat, logisztika, és a sort hosszan lehetne még folytatni.

Egyik kedvenc feladványom a könyvből a körforgalmas úthálózatok optimális tervezéséről szól. Egy közlekedési csomópontot többféle módon meg lehet oldani: aluljárókkal és felüljárókkal, lámpás kereszteződésekkel vagy körforgalmakkal. A körforgalmak előnye a lámpás kereszteződésekhez képest, hogy gyér forgalomban nem kell az autósoknak várakozniuk, az aluljárókhoz és felüljárókhoz képest pedig jelentősen olcsóbbak. Hátrányuk, hogy több a baleset lehetősége, ezért ennek mértékét szeretnénk már a tervezésnél optimalizálni.

Egy csomóponton – például egy körforgalmon – keresztülmenő útvonalhoz (valójában a sávvonal kifejezés helyesebb lenne jelen esetben) hozzárendelhetünk egy úgynevezett veszélyszámot, ami nem más, mint a becsatlakozási lehetőségek száma az útvonal mentén. Ha például az alábbi körforgalomba az 1. útról hajt fel valaki és a 3. úton hajt le, akkor a veszélyszám 2, mert a felhajtásnál balról nekimehetnek, majd a következő leágazásnál jobbról beléhajthatnak. A körforgalom elhagyása viszont nem növeli a veszélyszámot, mert a sávokat tekintve ott nincs becsatlakozási lehetőség, csak egy elágazás: a sofőr vagy továbbmegy, vagy kihajt a körforgalomból.

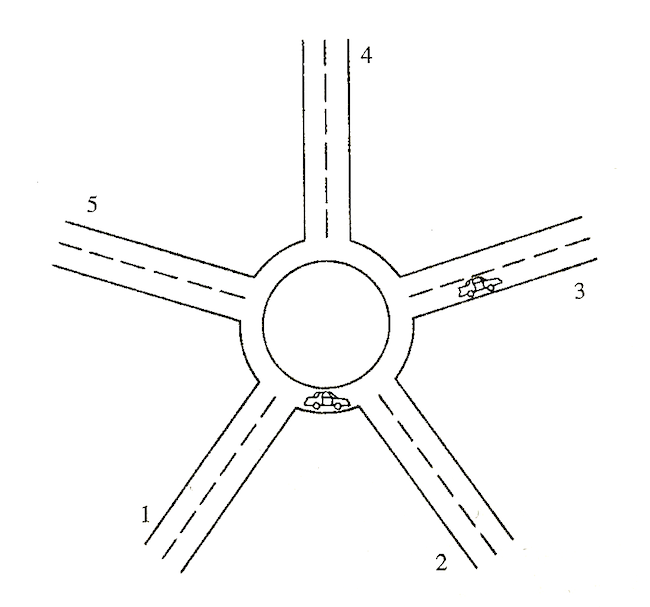
Ha egy autós nem tesz fölösleges köröket, és nem értelmetlenül hajt be a körforgalomba (azaz nem akar ugyanott kihajtani, ahol bejött), akkor a maximális veszélyszám a körforgalomba csatlakozó utak számánál éppen eggyel kevesebb. A fenti esetben az 1. útról felhajtó autósnak akkor lesz a legnagyobb a veszélyszáma, ha az 5. úton hajt le. Természetesen feltettük, hogy az utak kétsávosak, a körforgalom pedig egysávos, ahogy az illusztráló ábrán is látható.

194. feladvány: Körforgalmak

A könyvben szereplő feladványban olyan csomópontot kell tervezni, amelyben 12 kétsávos út találkozik össze. Úgy kell összekötnünk az utakat, hogy bámelyik útról bármelyik másikra is akarjon valaki átmenni, minél kisebb legyen a maximális veszélyszám. Ha például építenénk egyetlen nagy körforgalmat, akkor a maximális veszélyszám a fentiek alapján 11 lenne. Egy másik lehetőség, ha összekötünk két hatágú körforgalmat egy kétsávos extra úttal, de ebben az esetben az a furcsaság adódik, hogy a helyzet még rosszabb lesz. Ellenőrizzétek le, a maximális veszélyszáma ennek a konstrukciónak 12 lenne. A könyvben ugyanakkor találunk olyan konstrukciót, amelynek maximális veszélyszáma csupán 9.

A te feladatod viszont az, hogy olyan pályázatot nyújts be a közlekedési hatósághoz, amely legalább két lényegesen különböző tervet tartalmaz 9-es maximális veszélyszámmal. A tervben nem szerepelhetnek aluljárók, felüljárók, sem pedig kereszteződések. Két terv lényegesen különböző, ha az úthálózat gráfja más, például az útszakaszok száma vagy mondjuk az elágazások száma eltérő. Fölösleges útszakaszokat természetesen nem rakhatunk a tervbe. A maximális veszélyszám meghatározásánál tegyük fel, hogy mindenki az optimális úton megy, és nem akar ugyanazon az úton távozni, ahol beérkezik a csomópontba.

Bónusz kérdés haladóknak: Lejjebb lehet-e még szorítani 8-ra a maximális veszélyszámot? Mi a helyzet kisebb csomópontokra? 12-nél kisebb N-ekre meg tudjátok optimálisan tervezni N út találkozását?

Nehézségi szint:

A megfejtéseket részletes magyarázattal és a szükséges ábrákkal együtt az eszventura@qubit.hu címre várjuk. A leggyorsabb és legkreatívabb megoldást küldő versenyzőink felkerülnek az Ész Ventura dicsőségfalára – közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. A versenyről minden tudnivaló megtalálható: itt. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: november 30. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.