Hogyan lesz garantáltan szerencsés az éved?
Bűvösnek vagy mágikusnak nevezett négyzeteket már időszámításunk előtt is ismertek. A közvetlenül egymást követő különböző egész számokkal kitöltött n×n-es négyzetet bűvös négyzetnek nevezzük, ha a számok összege minden sorban, minden oszlopban és a két átlóban is ugyanaz. A világ számos táján találhatunk ilyen tulajdonságokkal rendelkező különböző méretű négyzeteket amuletteken és talizmánokon, ezeket a matematikai különlegességeket ugyanis több kultúrában is mágikus tulajdonságokkal ruházták fel.
Egy ilyen talizmánt ábrázol például Albrecht Dürer Melankólia I. című híres rézmetszete, ahol a Jupiter pecsétjének nevezett 4×4-es bűvös négyzet alsó sorának középső két számát összeolvasva még a készítés éve is kiolvasható. Ha szeretnéd, hogy a 2025-ös éved szerencsés legyen, akkor neked sincs más dolgod, mint alkotni egy bűvös négyzetet, és a legjobb az lenne, ha az 1-től 2025-ig terjedő számokkal töltenéd ki.
228. feladvány: 45×45-ös bűvös négyzet
2025 = 45 × 45, vagyis négyzetszám. Ez azt jelenti, hogy egy 45 sorból és 45 oszlopból álló táblázatba, azaz négyzetrácsba be tudjuk írni 1-től 2025-ig a számokat úgy, hogy az éppen tele legyen. De be lehet-e úgy írni ezeket a számokat, hogy minden sornak, minden oszlopnak és a két átlónak az összege is ugyanaz legyen?
Tipp chevron_down
Ismerkedjünk meg pár egyszerű bűvös négyzettel, és gondolkodjunk el azon, hogy egy n×n-es és egy m×m-es bűvös négyzetből lehet-e gyártani egy (n × m) × (n × m) méretű nagyobbat?
Megoldás chevron_down
Ha veszünk két bűvös négyzetet, akkor azokból készíthetünk egy nagyobbat. Ha például veszünk két 3×3-asat, akkor azokból készíthetünk egy 9×9-eset, és a két 3×3-as lehet egyforma is. Nagyon szemléletes videót is találhatunk a neten, ami ennek a folyamatát szépen bemutatja az alábbi ábrán bal oldalon látható 3×3-as négyzettel (illetve a videóban ennek a tükörképe szerepel).
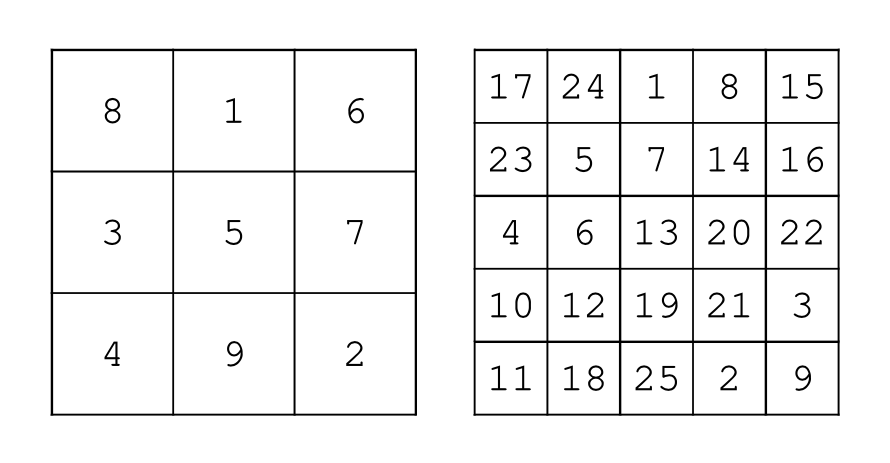
Ezek után a videóban kapott 9×9-es bűvös négyzetből és a fenti ábrán látható 5×5-ös bűvös négyzetből teljesen hasonló módon gyárthatunk egy 45×45-ös bűvös négyzetet, kihasználva azt, hogy 45 = 9×5. Ehhez először vesszük az 5×5-ös négyzetet, és a 2-es számot lecseréljük benne (81+1)-re, a 3-as számot (2·81+1)-re, a 4-es számot (3·81+1)-re és így tovább, míg végül a 25-ös számot is lecseréljük (24·81+1)-re. Az 1-es számot tartalmazó mezőt nem bántjuk. Így továbbra is bűvös marad a négyzet, annyi különbséggel, hogy nem közvetlenül egymást követő számok alkotják, hanem az egymást követő számok között éppen 81 lesz a különbség. Az eredeti 5×5-ös bűvös négyzetben a sorok és oszlop összege 65 volt, az újban 4865 lesz, mert (65-5)·81-el megnövekszik.
Ezek után vesszük az így kapott 5×5-ös négyzet minden mezőjét, és kicseréljük őket 9×9-es bűvös négyzetekre, mintha tovább osztanánk a mezőket, így egy 45×45-ös négyzetet fogunk kapni. A csere a következőképpen történik. Vesszük az 5×5-ös négyzetnek azt a celláját, amiben az 1-es szám van, és ezt lecseréljük a videóban kapott 9×9-es bűvös négyzetre. Ezután vesszük az 5×5-ös négyzetnek azt a celláját, amiben a 2-es szám van, és ezt lecseréljük egy olyan 9×9-es bűvös négyzetre, aminek minden elemét 81-el megnöveltük. Ezután vesszük az 5×5-ös négyzetnek azt a celláját, amiben a 3-as szám van, és ezt lecseréljük egy olyan 9×9-es bűvös négyzetre, aminek minden elemét az előzőhöz képest is megnöveljük még 81-el, és így tovább.
Amit kapunk, az bűvös négyzet lesz, hiszen a sorok és oszlopok öt darab 9×9-es bűvös négyzet soraiból és oszlopaiból fognak összeállni, ahogy a két átló is, és könnyen látható, hogy ezek az összegek ugyanakkorák lesznek, mert arányosan növeltük a cellák értékeit. Másrészt a 45×45-ös négyzetbe éppen egymást követő számok fognak kerülni 1-től 2025-ig, mert az 5×5-ös bűvös négyzetben szereplő 1-es szám helyére kerülő 9×9-es bűvös négyzetben 1-től 81-ig futnak a számok, a 2-es szám helyére kerülőben pedig (81+1)-től kezdődnek, és így tovább. Sajnos ilyen sok szám ábrázolása nem igazán férne el a képernyőn, ezért csak a mintázatot tudjuk bemutatni, lásd alább, sőt még itt se látszódik minden mező, mert a 3×3-as részmátrixokban már túl közeliek a számok, és azok azonos színűnek látszanak.
A feladat kérdésére a válasz tehát az, hogy lehetséges olyan bűvös négyzetet készíteni, amiben 1-től 2025-ig szerepelnek a számok, mert mutattunk erre egy lehetséges konstrukciót. Persze több különböző módszer is létezik, és rengeteg más jellegű bűvös négyzet is létrehozható, akár 45×45-ös mérteben. Alkosd meg a te saját egyedi bűvös négyzetedet, hogy csak neked hozzon szerencsét! A legnagyobb szerencsét akkor hozza, ha kézzel kerül kitöltésre, és a dokumentációt elkülditek az eszventura@qubit.hu címre.
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.