Az előző heti feladványhoz nagyon kitartónak kellett lenni, sok trükkös kör volt az ábrán, és senki nem találta meg elsőre az összeset. Boros Péter jóvoltából, akinek az animációt is köszönhetjük, itt látható alább az összes kör, amik tartalmaznak legalább négy pontot. A kérdés azonban nem a körök, hanem a pontnégyesek száma volt. Ezek között van olyan kör, amelyik négynél több pontot is tartalmaz, például a 6. sor 3. köre 7 pontot is a t-betűből, ezért az 35 különböző pontnégyest jelent, a 4. sor 3. köre pedig 5 pontot ugyancsak a t-betűből, ez 5 különböző pontnégyesnek felel meg. Így jön ki összesen az alábbi 21 körből 19+35+5 = 59 pontnégyes.

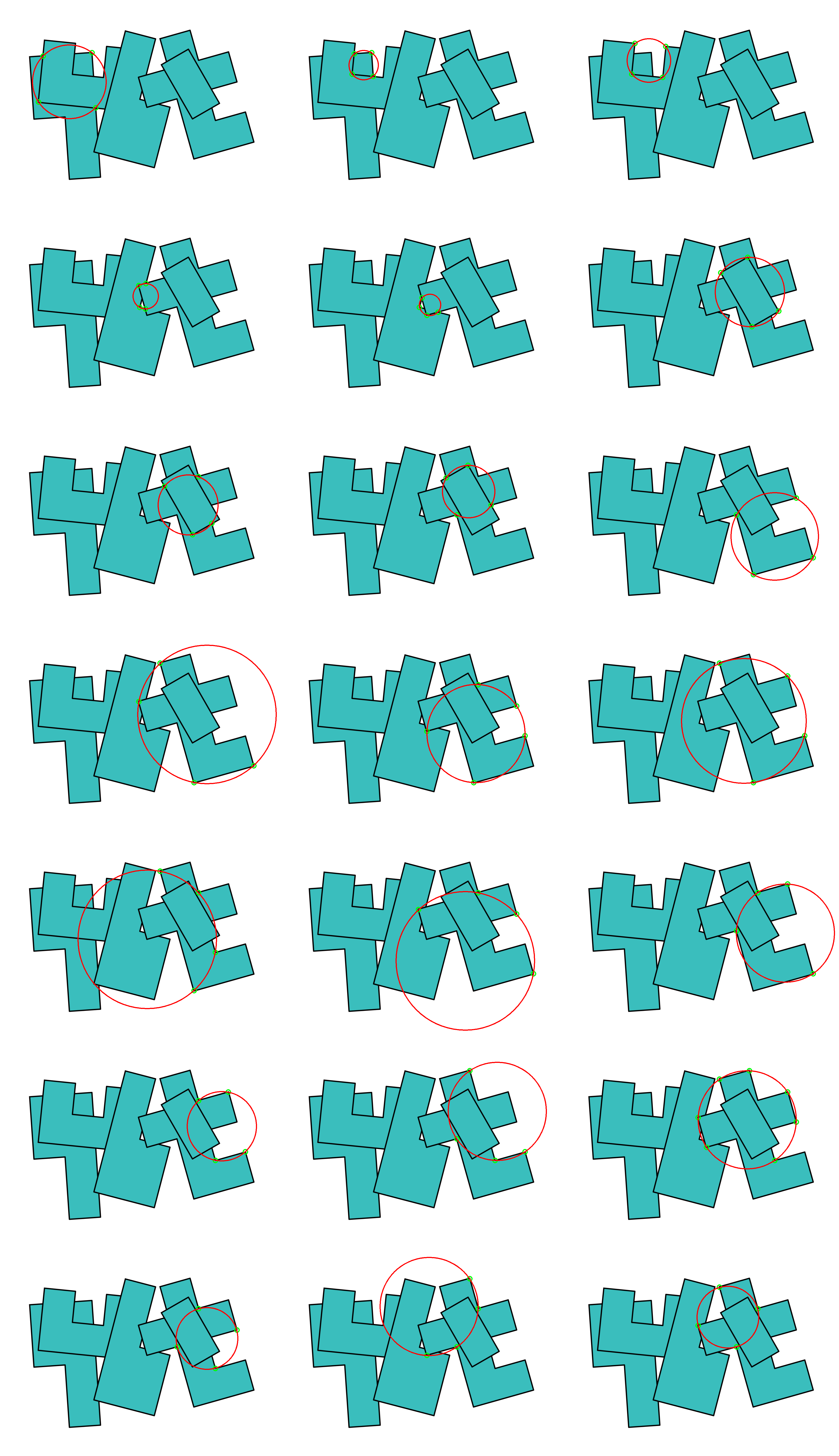
De nézzük melyek voltak ezek közül a legtrükkösebbek. Először is szögezzük le, hogy amit keresünk, azok ún. húrnégyszögek. A legegyszerűbb húrnégyszög a négyzet, a téglalap és az egyenlő szárú trapéz, ezeket volt a legkönnyebb megtalálni, bár ezek közül is nehezebb észrevenni a rácshoz képest döntött példányokat. Egy húrnégyszög azonban nem feltétlenül kell szimmetrikus legyen. Mint ismeretes, a húrnégyszögség szükséges és elégséges feltétele, hogy szemközti szögeinek összege 180 fok legyen, tehát például két (azonos hosszúságú) átfogójával egymásnak fordított tetszőleges derékszögű háromszög húrnégyszöget alkot, de erre még visszatérünk.

Azt könnyű volt végignézni, hogy az egyes betűk látható csúcsai betűnként hány kört határoznak meg. A q betű egyet sem, az u-betű csak egyet, lásd 1. sor 3. kör, a b betű szintén nem határoz meg egyet sem, az i betű nyilvánvalóan csak egyet. A t betűnél volt a legnehezebb leszámolni, mert 12 látható csúcsa volt, amiből 4 pontot (12*11*10*9)/(4*3*2) = 495 féle képpen lehet kiválasztani. Kellett tehát találni valamilyen módot arra, hogy ezeket az ember szisztematikusan sorra vegye, vagy ezekből sokat kizárjon alapból.

Volt, aki erre számítógépes programot írt, és a rácskoordináták alapján analitikusan meg tudta határozni az összes kört. Mások olyan programot írtak, amelyik grafikusan próbálja a lehetséges köröket meghatározni a kép alapján. Ez utóbbi esetben a program eredménye függ a kép pixelfelbontásától, így az eredmény csak segítségként használható ahhoz, hogy aztán geometriai megfontolásokkal belássuk, a megtalált körök közül melyik felel meg ténylegesen a feladat feltételeinek.

De természetesen program nélkül is meg lehetett oldani a leszámolást. Egy lehetséges metódus az, hogy előbb egy négyzetrácsos papíron sugár szerint növekvő sorrendben felrajzoljuk azokat a rácsköröket, amik átmennek legalább négy rácsponton egy szóba jöhető maximális méretig. Majd ezeket, ill. eltoltjaikat megpróbáljuk a t-betűre illeszteni.

Thalész-tétel

Na de menjünk tovább! Nagyon sokan azt gondolták (esetleg hibásan bizonyították), hogy húrnégyszögeket csak betűnként külön érdemes keresnünk, és a metszéspontok nem jöhetnek szóba, mert véletlenszerűek. Ez nem igaz, ha ugyanis egy betű egyik sarka nemcsak a másik betű oldalába metsz bele, hanem annak sarkába, vagy egymásra merőleges oldalaiba, akkor a geometria egyik legrégebbi tétele, az ún. Thalész-tétel alapján találhatunk nem szimmetrikus húrnégyszögeket is, például olyant, amelynek két szemközti szöge derékszög, lásd 1. sor 1. és 2. ábra a q és u betűk metszésénél. De akár olyant is, ahol a húrnégyszög egyik szöge sem derékszög, mert a derékszögű háromszögek nem egymással szembe vannak fordítva, hanem az átfogóra emelt Thalész-kör azonos oldalára esnek, lásd 2. sor 1. és 2. ábra a b és t betűk metszésénél. És van még az i és t betűk metszésénél is, lásd 3. sor 1. és 2. ábra, ezeket volt talán a legnehezebb észrevenni, mert itt a metszett oldalak merőlegessége nem abból adódik, hogy az oldalak közvetlenül egy sarokhoz tartoznak.

Köszönet mindenkinek a fáradozásért, reméljük hasznos volt. Úgy hallottam, hogy az Ész Ventura példáit a matektanárok is szeretik és némelyiket beviszik a gyerekeknek órára. Ez a példa szerintem kiváltképp alkalmas ilyen célra, hiszen nagyon sokrétű, és sokat lehet tanulni belőle. Van benne rácsgeometria, véletlenszerűség értelmezése, kombinatorika, Thalész-tétel, és kellett sok kitartás és rendszerező gondolkodás is a megoldáshoz. Ilyen feladatból természetesen egyszerűbbet is lehet készíteni. Elárulom, hogy az inspiráció eredetileg Martin Gardner egyik könyvéből származik, ahol téglalap alakú papírok és pénzérmék voltak egymásra dobálva.

A legjobb megoldások beküldőit meg lehet tekinteni a frissített dicsőségfalon. Az ott szereplők között év végén ajándékokat sorsolunk ki, ami hamarosan elérkezik. A részletes szabályokat a dicsőségfal alatt el lehet olvasni. További jó rejtvényfejtést a következő feladványhoz. Ígérem, most egy könnyebb következik!