Az előző feladványban egy 45 fokos körívek által feldarabolt körcikkben kellett a piros és kék területek arányát meghatározni. A kérdéses területek könnyen számolhatók, de a megoldáshoz még erre sem volt szükség. Kétségkívül a legegyszerűbb és egyben a legszebb megoldás az alábbi.

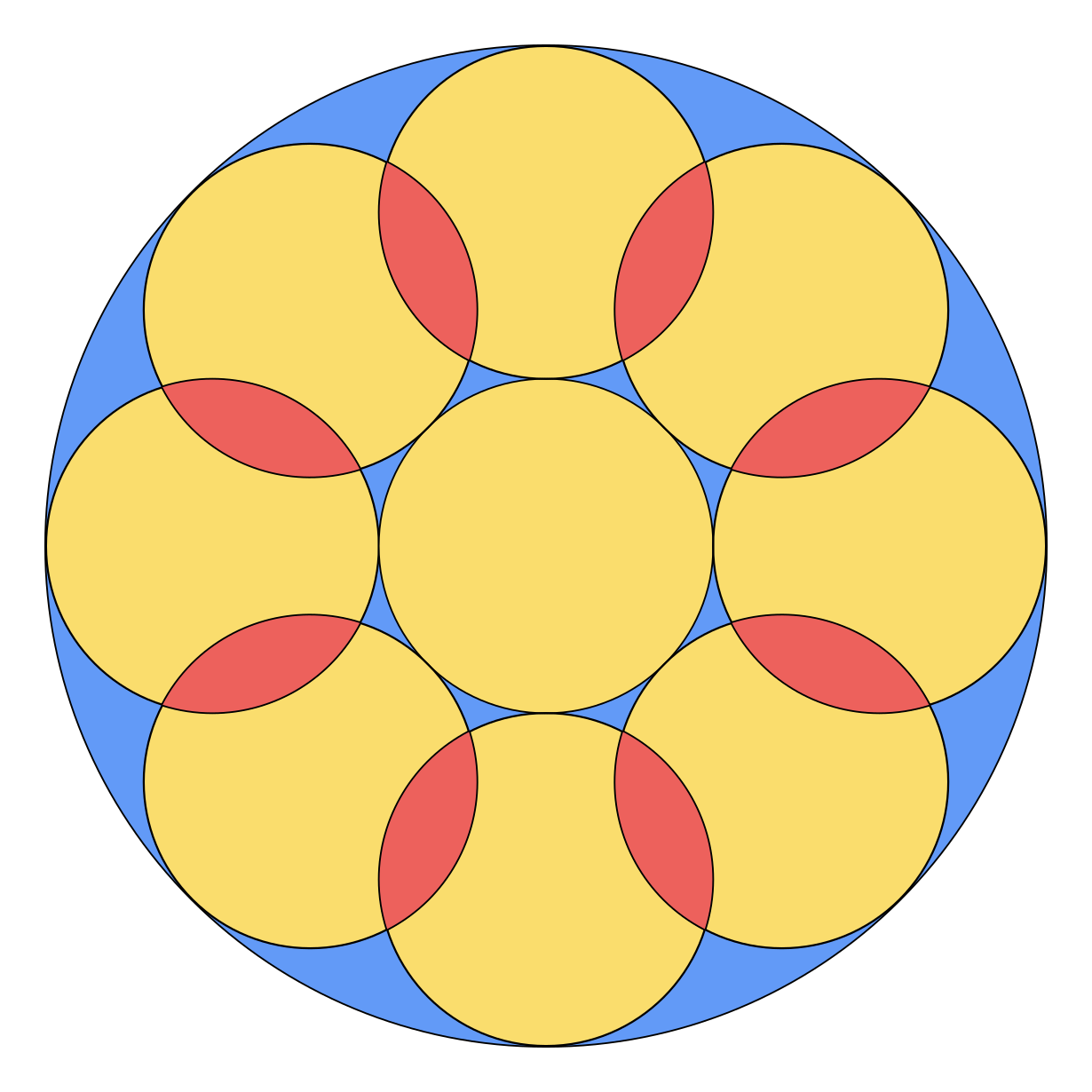
A feladatban megadott piteszeletből vegyünk nyolc egyforma darabot, és ezekből illesszünk össze egy teljes nagy pitetortát, így kapjuk a fenti rozetta mintázatot. A nagy kör sugara egy kis kör sugarának háromszorosa, ezért a nagy kör területe a kis kör területének kilencszerese, magyarán kilenc kis kör összterülete éppen kiadja a nagy kör területét. Az ábrán azonban éppen kilenc kis kör szerepel a nagy körön belül, ez csak úgy lehetséges, ha a kimaradó kék régiók területe éppen megegyezik az átfedő piros területekkel, és ez az eredeti piteszeletekre vonatkoztatva is igaz lesz.

Megjegyzés: itt található a feladványnak egy egyszerűbb változata, aminek a megoldása ugyanerre a kaptafára működik.

Haladóknak továbbgondolásra: a fenti két feladványon kívül lehet-e még további hasonló elven működő szép feladványokat kreálni, ha megköveteljük, hogy a nagy kör sugara egy kis kör sugarának többszöröse legyen? Aki ezzel kapcsolatosan el szeretné küldeni észrevételeit, megteheti a szokásos eszventura@qubit.hu címre küldve. Az e-mail subject mezőjébe kérjük feltüntetni, hogy 14. feladvány – kiegészítés.