Korábbi cikkemben azt írtam, hogy a filatéliának nem sok köze van a kombinatorikához, de ez nem teljesen igaz. Van ugyanis a kombinatorikának egy igen nehéz kérdése, ami pont a bélyegekhez kapcsolódik, pontosabban azok hajtogatásához. Ha megkérdezzük, hogy egy N darab bélyeget tartalmazó bélyegcsíkot hányféleképpen tudunk összehajtani úgy a perforációk mentén, hogy a végén az összes bélyeg egymáson legyen egy stócban, akkor ez egy nehéz kérdés.

Mit jelent az (a kombinatorikában), hogy nehéz kérdés?

Kis N-re persze könnyen össze tudjuk számolni. Két egymás melletti bélyeg esetén például két lehetőség van: vagy az első bélyeg elé, vagy mögé hajtjuk a másikat. Azt is mondhatnánk origamis kifejezéssel élve, hogy vagy ún. völgyhajtást csinálunk, vagy hegyhajtást az egyetlen perforált él mentén, ami a két bélyeget összeköti. A két stóc abban különbözik egymástól, hogy az egyikben a bélyegek nyomtatott felei érintkeznek egymással, míg a másikban a ragasztós feleik.

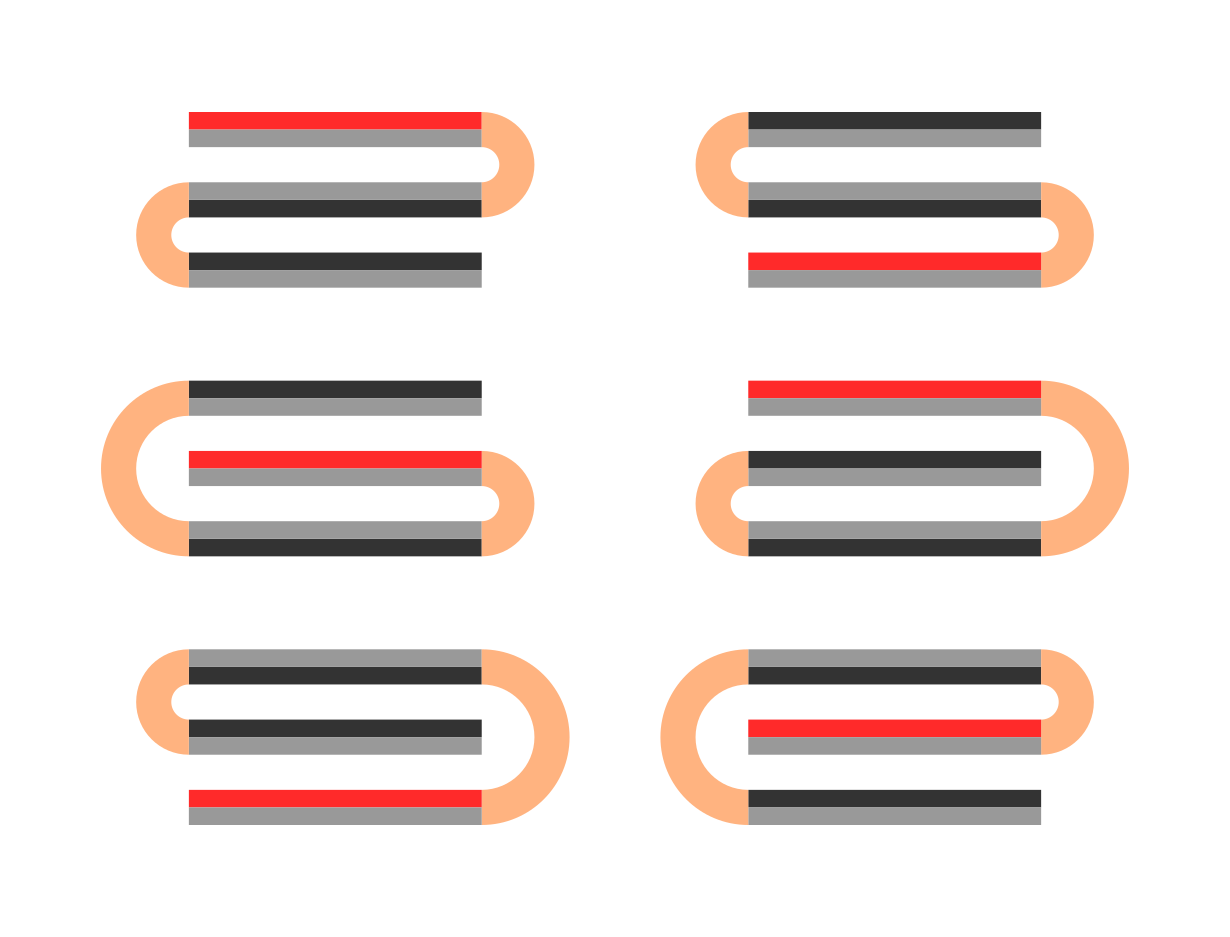
Három hosszú bélyegcsík esetén a variációk száma hat, lásd az alábbi oldalnézeti ábrát, ahol a bélyegek nyomtatott felét sötét réteg jelzi, a ragasztós felét halvány szürke, pirossal pedig a bélyegsor legelső bélyegét jelöltük. Ha végignézzük a variációkat, láthatjuk, hogy a három bélyeg tetszőleges rétegsorrendje kihozható megfelelő hajtogatással, ez azonban N > 3 esetén már nem lesz így. Előfordulhat ugyanis olyan sorrend, amelyet megvalósító hajtogatásban az ábrán narancssárgával jelölt perforációs összeköttetések metszenék egymást, azaz fizikailag nem lenne megvalósítható.

A nehézséget az jelenti, hogy ennek a problémának a megoldására nem ismert olyan képlet, ami N függvényében megadná a végeredményt. De nemcsak hogy nem találtunk még rá képletet; hatékony algoritmust se talált még senki. Hatékony alatt olyan algoritmust értünk, ami nagyobb N-re is le tudna futni kivárható időn belül, azaz N függvényében polinomiális idő alatt lefut, vagyis a futásidő N valahanyadik hatványánál nem nő gyorsabban. Csak olyan algoritmust ismerünk, ami lényegében egyesével végignézi az összes lehetséges esetet, ennek azonban a futási ideje exponenciálisan növekszik N-el, mert N darab bélyeg lehetséges sorrendjeinek a száma kombinatorikusan felrobban. Erről a jelenségről volt már szó a bélyegek darabolásánál is. Nem véletlen, hogy számítógéppel is csak N = 29 -ig tudták eddig kiszámítani a választ erre a kérdésre.

De a probléma még ennél is nehezebb. Nemcsak kiszámolni nem tudjuk, de még megbecsülni se. Nem ismerünk se alsó, se felső nem triviális korlátot, és éppen ezért a függvény menetét, azaz tendenciáját se tudjuk megbecsülni. Matematikusok azt szokták erre mondani, hogy nem ismerjük az aszimptotikus viselkedését, vagyis azt, hogy nagy N-re kb. milyen mértékben növekszik a függvény. Maradunk tehát kis számú bélyegnél – ami azonban nehézzé fogja tenni az alábbi feladványt, az a bélyegívek alakja lesz.

17. feladvány: Betűhajtogatások

Az a kérdés, hogy hányféleképpen lehet összehajtogatni perforációk mentén az alábbi betűket egyetlen bélyegnyi alapterületű stócba? A beküldőknek elegendő egy tetszőleges betűt kiválasztaniuk az alábbiak közül, kivéve az I-betűt, amire a megoldás fentebb már szerepelt. Haladóknak viszont bónusz pontokért lehet akár az összes is!

Felajánlott koponyák:

A megfejtéseket az eszventura@qubit.hu címre várjuk. A megoldáshoz kérünk indoklást mellékelni, ha szükséges, akkor ábrával együtt! A legelső megoldók és a legjobb versenyzők felkerülnek az Ész Ventura dicsőségfalára, aki nem kíván ott szerepelni, kérjük, jelezze. Szerepelni álnévvel is lehet, ezért mindenképpen érdemes az év végén kisorsolt nyeremények miatt. Leveleiket kérjük, ékezetesen írják alá. Az e-mail subject mezőjében kérjük feltüntetni, hogy 'megoldás', illetve sorszámmal jelezni, hogy melyik feladványról van szó. Beküldési határidő: április 25-e éjfél.