Minden mindennel összefügg! Ezt most nem fogom bizonyítani, de milyen érdekes például az, hogy nemrég volt szó hajtogatásról, legutóbb pedig körpakolásról, és ez a két látszólag nagyon távoli dolog is összefügg. Az hogy a képen szereplő parázsbogarat egy origamimester meg tudja hajtogatni, abban a körpakolás matematikája fontos szerepet játszik. De ne szaladjunk ennyire előre, ismerkedjünk meg egy kicsit az origami történetével.

Japánul ori = hajtogatás, kami = papír, innen a szó eredete, bár az origami ősi művészete valószínűleg Kínából származik, a modern időkben azonban Japánban fejlesztették tökélyre és onnan terjedt el. Az origami ma is mélyen gyökerezik a japán kultúrában. A hagyomány szerint ha valaki 1000 darut hajtogat, ami az örök fiatalság, boldogság és jó szerencse szimbóluma, akkor a kívánsága valóra válik. Nem véletlen, hogy világszerte a legismertebb origami valószínűleg a darumadár, amit japánban az összes kisiskolás meg tud hajtogatni. Sajnos nem valószínű, hogy ez a magyar gyerekekre is elmondható, és általában felnőttként sem emlékszünk többre, mint a papírcsákóra és a papírrepülőre. Pedig a papírhajtogatás nagyon jó kézségfejlesztő, nem csak a kézügyességet javítja, de összehangolja a szem és a kéz munkáját, segíti a térérzékelést, megismerhetők általa az alapvető geometriai formák és fogalmak, fejleszti a kreativitást és a memóriát. És mindehhez csak egy darab papírra van szükség.

Az origami azonban nem csak gyerekjáték és szórakozás lehet, hanem egy komoly művészeti forma is. Az internet korában nagyon sokakhoz eljutottak olyan origami-diagramok, amik egy speciális jelölésrendszerrel írják le a hajtogatásokat. Ez a nyelvezet megkönnyítette a kommunikációt és a tudás átadását, az alkotók inspirálták egymást, továbbfejlesztették a meglévő formákat, és ma már rengeteg gyönyörű, komplex és technikailag is extrém alkotást láthatunk, ha körbenézünk a neten. Ezt alátámasztandó nem is szeretnék belinkelni semmit, mert olyan sok origamimester és elképesztő alkotás van világszerte, hogy nehéz lenne közülük választani, amúgy is bizonyára mindenki találkozott már hasonlókkal, vagy ha mégsem, akkor most könnyedén rákereshet a neten. Hogy mennyire népszerű az origami, azt amúgy az is mutatja, hogy a Japán Origami Szövetség nem kevesebb, mint tízezer tagot számlál a világ minden részéből.

Se olló, se ragasztó

Az origaminak rengeteg különböző stílusa és fajtája létezik, amikről külön is érdemes lenne beszélni, de alapvető megkötés szokott lenni, hogy egy négyzet alakú papírból kell kiindulni és nem szabad se vágni, se ragasztani. Mármost felmerül a kérdés, hogy ilyen feltételek mellett mi az, amit meg lehet csinálni. Egy korlátozó tényező lehet a rétegek száma. Elképzelhető ugyanis, hogy bár elvileg meghajtogatható lenne valami, de olyan sok rétegben kellene egymásra hajtani a papírt, hogy az fizikailag már nem megvalósítható. Próbáljátok csak ki, hogy hányszor tudtok egy papírt kettéhajtani. Mielőtt nekiláttok, becsüljétek meg. Sikerült eltalálni? Ha azonban ettől eltekintünk, akkor az a nagy kérdés, hogy miként lehet egy kigondolt formát létrehozni. Ez a tudás korábban csak a jó térlátással és nagy tapasztalattal rendelkező origamimesterek sajátja volt, ma azonban ebben már segít a matematika.

Nézzük, hogyan is kéne nekiállni egy a fenti képen is látható parázsbogár meghajtogatásának. Vázlatosan meg kell nézni a bogár felépítését, és egy pálcikarajzot készíteni a végtagokkal vagy egyéb nyúlványokkal. Először ennek a pálcikamodellnek megfelelő elnagyolt papírmodellt kell elkészíteni, amiben minden nyúlványnak megfelel egy lifegő rész. Ezután tulajdonképpen már egyszerű a befejezés, vannak ugyan technikai fortélyok, de ha ezt az alap vázt odaadnánk egy kezdőnek, tulajdonképpen ő is ki tudná már belőle úgy alakítani a végtagokat, hogy az állat felismerhető legyen, mert csak picit kell alakítgatni a lifegő részeken. A procedúrában a nehéz lépés az, hogy kitaláljuk azt a hajtogatási diagramot, amit követve előáll az elképzelt pálcikamodell lapos, de a megfelelő lifegő részeket már tartalmazó, papír alapú megvalósítása. Robert J. Lang amerikai fizikus és origamiművész az origami matematikájának megértése után a körpakolás segítségével megalkotott erre egy automatikus módszert, amit a TreeMaker nevű ingyenesen elérhető programmal bárki tud alkalmazni.

De hogyan jön ide a körpakolás?

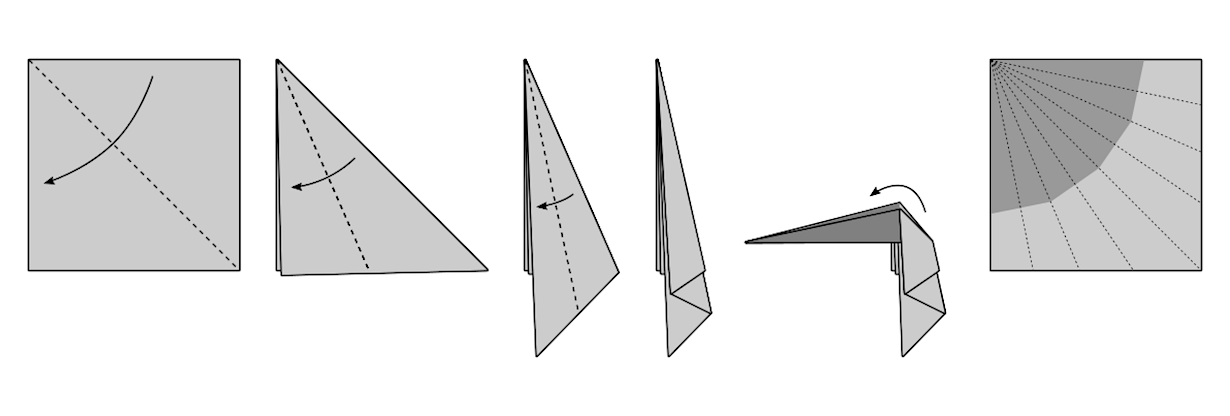
Gondoljunk bele, hogy mennyi helyet foglal a papírunkból egy végtag, vagy bármilyen nyúlvány. Vegyük az egyszerűség kedvéért egy papírlap sarkát, és kezdjük a derékszöget felezni, és egyre hegyesebb szöget hajtogatni a sarokból úgy, hogy a rétegeket egymásra hajtjuk. Ha megálltunk, akkor a hegyes csúcs egy részét törjük meg derékszögben úgy, hogy abban minden réteg benne legyen, majd hajtsuk ki a papírt. A behajtott hegyes csúcsot alkotó papír területét sötétszürkével jelöltük az ábrán, ez egy sokszög lesz, ami annál jobban közelít egy negyedkört, minél keskenyebb volt a hegyesszög. Ha pedig egy ilyen nyúlványt a papír élén alakítanánk ki, vagy a papír közepén, akkor félkört vagy teljes kört fedne le a kialakításához szükséges területrész. Ennyi bevezető után nézzük az e heti feladványt.

19. feladvány: Parázsbogár-origami

Az alábbi fotón látható parázsbogár papírból meghajtott modellje Derek McGunn munkáját dícséri. Ezúton is köszönet neki, hogy rendelkezésünkre bocsátotta a fotót. Tegyük fel, hogy a bogár ún. fésűs csápján található 2 × 16 szőrszál mindegyikének hossza egyenként 1 hüvelyk, a hat láb, a két szárny és a potroh hossza pedig mindegyik 3 hüvelyk a tövétől a végéig. Mutassuk meg, hogy ebben az esetben a felhasznált négyzet alakú papír oldalhossza legalább 12 hüvelyk volt! Megjegyzés: ennek belátásához elég annyit tudni az origamiról, ami fentebb ismertetésre került! Haladóknak: azt is be tudnátok látni, hogy legalább 13, 14, 15, esetleg 16 hüvelyk volt?

Felajánlott koponyák száma:

A megfejtéseket az eszventura@qubit.hu címre várjuk. A megoldáshoz kérünk indoklást mellékelni, ha szükséges, akkor ábrával együtt! A legelső megoldók és a legjobb versenyzők felkerülnek az Ész Ventura dicsőségfalára, aki nem kíván ott szerepelni, kérjük, jelezze. Szerepelni álnévvel is lehet, ezért mindenképpen érdemes az év végén kisorsolt nyeremények miatt. Leveleiket kérjük, ékezetesen írják alá. Az e-mail subject mezőjében kérjük feltüntetni, hogy 'megoldás', illetve sorszámmal jelezni, hogy melyik feladványról van szó. Beküldési határidő: május 12. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, bűvész