Az utóbbi feladványban az volt a feladat, hogy a fák közötti minimális távolság betartása mellett lehető legkisebb kerületű ligetet konstruáljunk. Három fa esetén a megoldás egyértelmű, hiszen a fák egy olyan háromszöget feszítenek ki, aminek minden oldala legalább 10 méter, tehát a kerület legalább 30 méter, és ez igaz elfajult esetben is, ha a fák egy egyenesre esnek. Ez a minimális kerület pedig megvalósítható egy szabályos háromszöggel, aminek minden oldala pontosan 10 méter.

Azt is tudjuk, hogy szabályos háromszögekkel a sík hézagmentesen parkettázható, tehát több fa esetén érdemes lehet továbbra is a 10 méteres oldalú szabályos háromszögekből építkezni, és úgy egymás mellé pakolni őket, hogy megfelelő számú rácspontot (fák helyei) lefedjenek a háromszögrácsban, vagy más néven hexagonális rácsban. Hogy ez a hexagonális elrendezés a legsűrűbb rácselrendezés a végtelen síkra vonatkozóan, azt már Joseph Louis Lagrange bizonyította 1773-ban. Azt viszont, hogy az összes lehetséges szabályos és szabálytalan elrendezés között is a hexagonális rács a legsűrűbb a teljes síkra vonatkozóan, Fejes Tóth László bizonyította be helytállóan 1940-ben.

Mi persze nem akarjuk végtelen sok fával a teljes síkot beültetni. Véges sok fa esetén az optimális megoldás akár el is térhetne a rácstól, ráadásul mi nem pont a sűrűséget akarjuk maximalizálni, hanem a kerületet minimalizálni. Megjegyezzük egyébként, hogy a matematikának ezt a problémáját körpakolásnak szokták nevezni, és az említett matematikusok nem fák ültetését nézték, hanem körök átfedésmentes elhelyezését a síkon. A kettő azonban ekvivalens, ha a fák törzse köré öt méter sugarú köröket képzelünk (például a fák lombkoronáját, amit a fenti ábrán a zöld körlapok jelölnek) és megköveteljük, hogy a körlapok (azaz a lombkoronák) ne érjenek egymásba.

De ha el is fogadjuk, hogy rácsidomok között keressük a megoldást a háromszögrácson, még mindig kérdéses, hogy a sok lehetséges alakzat közül melyik lesz a legkisebb kerületű. Mivel a háromszögrácsra korlátozva magunkat valójában a fák sűrűségét rögzítettük, azért ez a kérdés a diszkrét verziója annak a kérdésnek, hogy adott területű síkidomok közül melyik kerülete a legkisebb a síkon. Ezzel talán már találkozott a kedves olvasó. A válasz a kör, amit hamar meg lehet sejteni némi próbálgatás után is. Az érdekesség az, hogy az állítás, amit a matematikában izoperimetrikus tételnek neveznek, nagyon egyszerűnek tűnik, de a bizonyítása komoly matematikai apparátust igényel. Ez alapján – vagy saját próbálgatásaink alapján – mindenesetre azt sejthetjük, hogy a megoldás olyan rácssokszög lehet, ami minél inkább körhöz hasonló.

Amit tehát keresünk, az olyasmi, mint egy raszteres kör. Mondanám, hogy pixeles kör a számítógép képernyőjén, de a monitorokon a pixelek négyzetrácsba vannak rendezve, nekünk pedig háromszög alakú pixelekből kell építkeznünk, tehát a háromszögrácson keresünk egy 90 rácspontot tartalmazó kört. Első körben próbálkozzunk szabályos elrendezéssel, azaz a kör középpontját tegyük egy rácspontra, vagy egy kis háromszög köréírható körének középpontjába. Megnézhetjük, hogy amint koncentrikusan növeljük a kört a középpontjából, hogyan változik a benne lévő rácspontok száma, és ha szerencsénk van, akkor az egyik fajta sorozatban lesz 90 rácspontot tartlamazó pixeles kör. Ezek egyébként ismert sorozatok: A038590 és A038588. Előbbiben nem szerepel a 90, csak a 91. Utóbbiban viszont szerepel a 90, és a hozzá tartozó raszteres kör az alábbi.

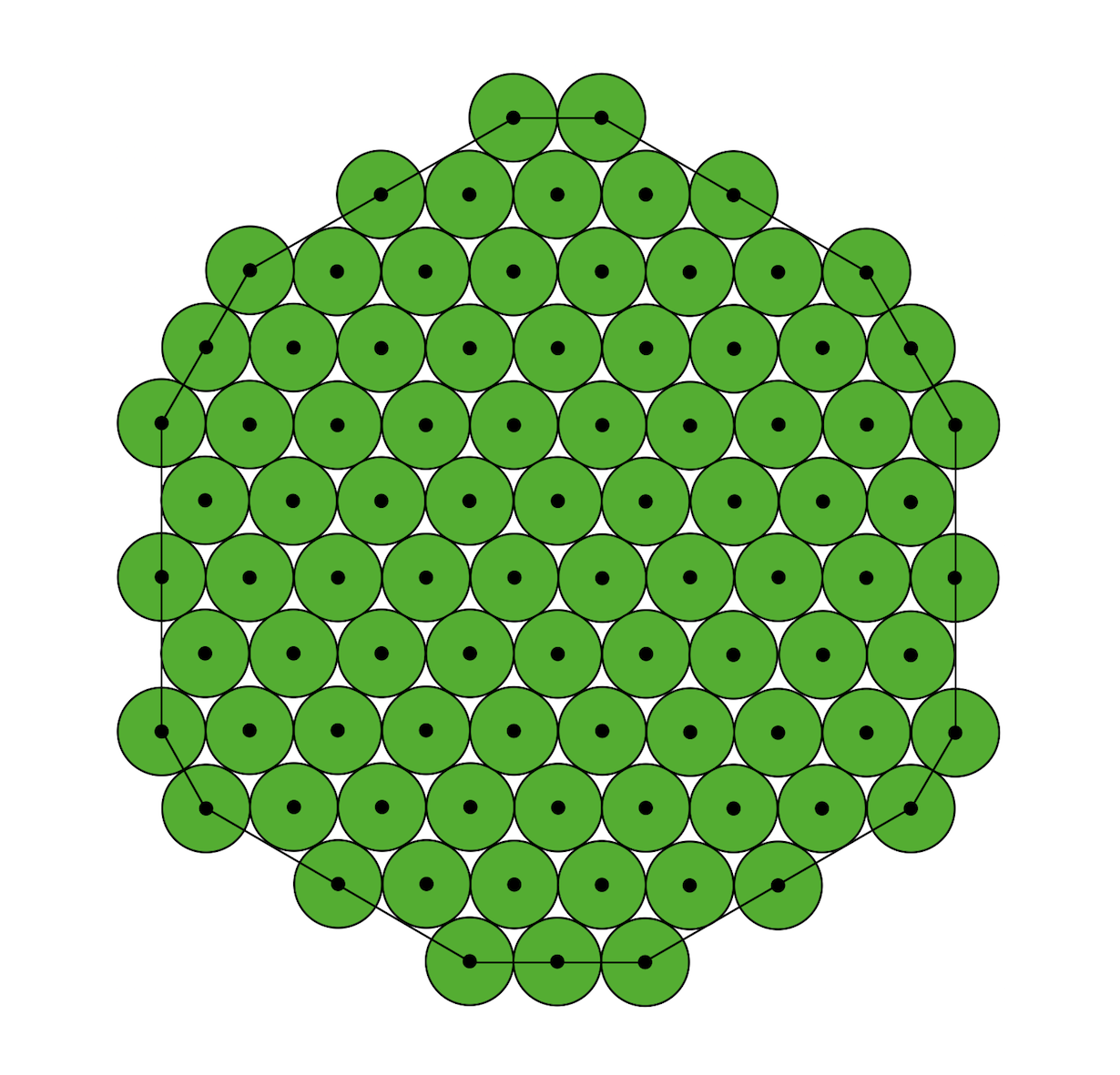
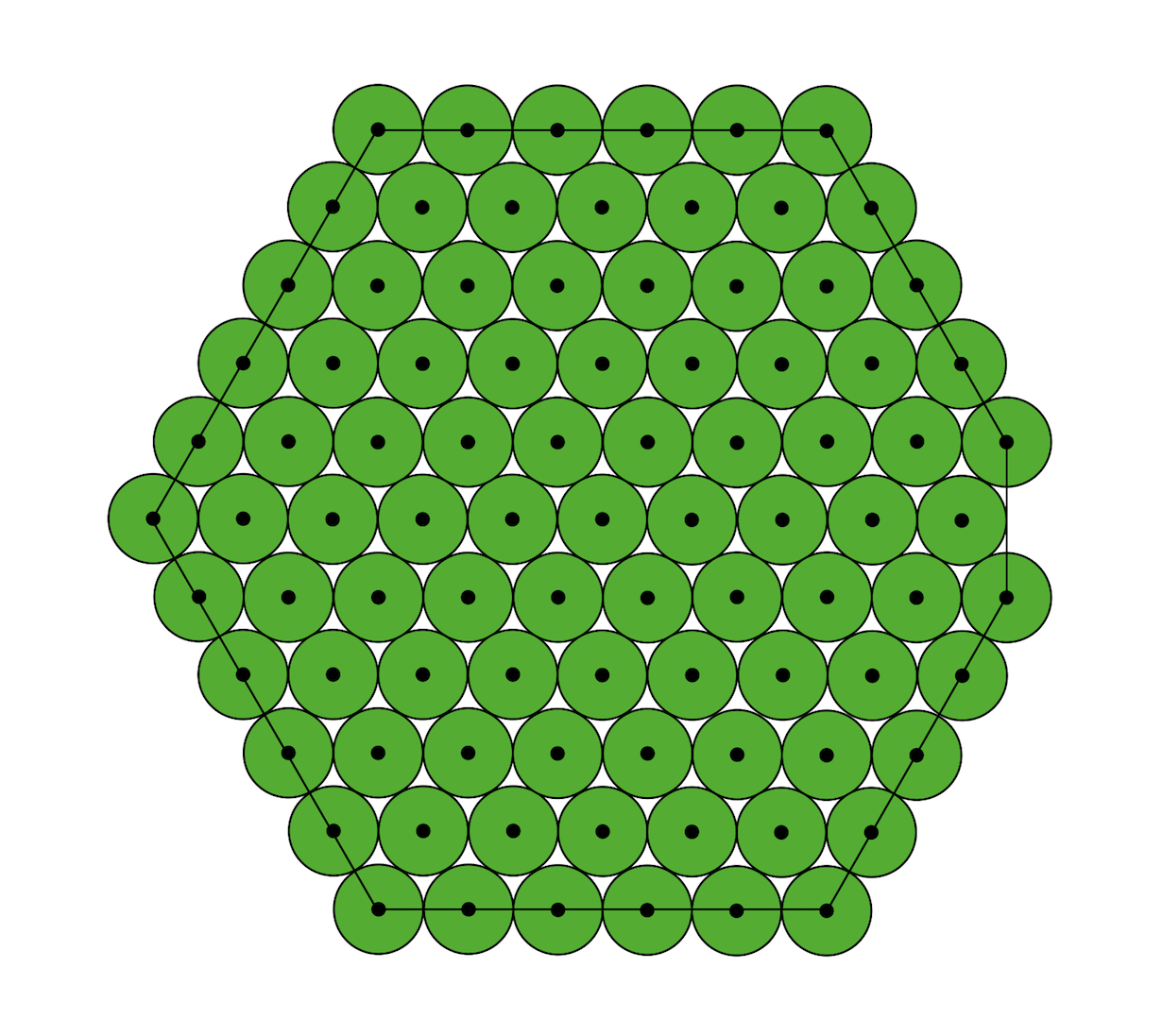
A fenti körnek a kerülete (9+12√3) × 10m ≈ 297,85 méter. Ha viszont nem ragaszkodunk a szimmetriához, akkor használhatjuk a másik sorozatból a 91 pontot tartalmazó raszteres kört is, ami pont egy 50 méter oldalú szabályos hatszögnek felel meg, lásd alább. Ennek a kerülete pont 6 × 50m = 300 méter lenne, de mivel egy pont fölösleges, ezért az egyik csúcsát elhagyhatjuk, így picikét csökkentjük a kerületet. A kerület pontosan (28+√3) × 10m ≈ 297,32 méter lesz, ami érdekes módon jobb, mint az előző forgásszimmetrikus verzió, de mindkettő 300 méter alatt marad.

Végül ismertetnék még egy megközelítési lehetőséget. Mint említettük, a körpakolási probléma megoldása ismert a végtelen síkra, de ha egy konkrét korlátos tartományt definiáló síkidomon belülre szeretnénk a lehető legtöbb egyforma kört fedésmentesen lepakolni, az egy igen nehéz probléma, aminek nincs általános megoldása. Kis számú körre és szokásos síkidomokra (kör, négyzet, félkör, stb.) léteznek bizonyított eredmények, de több kört tartalmazó pakolások esetében csak azt tudhatjuk, hogy mik az eddig talált legjobb megoldások. Ezek összegyűjtésére jött létre például a packomania.com weboldal.

A fenti oldalon a kör pakolása körbe részben megtudhatjuk, hogy 90 darab egyforma kör jelenleg ismert legtömöttebb elrendezése egy nagy körbe az alábbi struktúrában lehetséges, ahol a nagy kör sugara kb. 52,73 méter, ha a kis körök sugara 5 méter. A külső fák törzse azonban a nagy kör külső szélétől 5 méterrel beljebb esik mindenhol, azaz a fák törzsei egy 47,73 méter sugarú (a nagy körrel koncentrikus) körön belülre esnek, aminek a kerülete: 2 × 47,73m × π ≈ 299,9 méter, ami ugyancsak 300 méter alatt van. Továbbá ekkora kötélre nincs is szükség, mert a szomszédos kerületi fák törzsei között mehet egyenesen a kötél körív helyett. Ha az alábbi elrendezés konkrét koordinátáit megnézzük, ami a fenti oldalon hozzáférhető, akkor kiszámolhatjuk, hogy ebben az elrendezésben a fák egy 299,3 méter hosszú kötéllel is körbevehetők, de ez nem rövidebb, mint a korábbi szabályos háromszögrácsra illeszkedő megoldásaink.

Azt sajnos egyik beküldő sem tudta bizonyítani, hogy biztosan nem létezik olyan megoldás, amit (28+√3) × 10m ≈ 297,32 méternél rövidebb kötéllel körbe lehetne keríteni. Ezt a kérdést tehát nyitva hagyom, és határidőn túl is fogadok megoldásokat az elkövetkező 10-20 évben plusz pontokért!