Magyar kutatók: nyakunkon a második kvantumforradalom

Magyar, cseh és német kutatóknak elsőként sikerült olyan szimulációs eszközt kifejleszteniük, amely egy kvantumos bolyongást végző részecske viselkedésének összes alapvető aspektusát képes szimulálni.

A korábbi kísérletekben a részecskének csak a hullámjellegét sikerült reprodukálni. Az új kísérlet azonban, amelynek eredményéről közös tanulmányban számoltak be az MTA Wigner Fizikai Kutatóintézete, a Prágai Cseh Műszaki Egyetem és a németországi Paderborni Egyetem kutatói, a kvantummechanikai mérés hatását is képes szimulálni. A készülékkel elsőként azt vizsgálták meg, hogy a bolyongó részecske visszatér-e a kezdeti helyére a bolyongása során, vagy sem. A kutatóknak sikerült egy olyan elemet beépíteniük a kísérleti elrendezésbe, amely valódi kvantummechanikai mérést valósít meg. Ezzel közvetlenül meg tudták figyelni a kvantumos mérésnek a kvantumos bolyongóra gyakorolt hatását.

A kísérletet hagyományos, úgynevezett koherens fénnyel végezték a kutatók, akik szerint a berendezés lényegében változtatás nélkül alkalmazható lesz olyan kvantumos bolyongási kísérletek elvégzésére is, amelyekben a kvantumos bolyongót egyetlen foton személyesíti majd meg, ehhez csupán a fényforrást kell majd lecserélni. Ezáltal a kísérletben résztvevő három intézmény kutatói munkájukkal a jövő egyfotonos kísérleteinek egy különösen ígéretes irányát alapozták meg.

A kvantumtechnológia a kutatók szerint a második kvantumos forradalom közeledtét jelzi. „Egy megfelelően nagy kapacitású kvantumszimulátor lehetővé tenné a kvantummechanika által leírt folyamatok tanulmányozását, amelyeket praktikusan lehetetlen kezelni a jelenlegi, félvezető technológiára épített úgynevezett klasszikus számítógépekkel” – jósolja a tanulmány, amely a következő idővonalon vázolja a várható fejleményeket.

Hogyan bolyong, ami kvantumosan bolyong?

„A kvantumos bolyongás a véletlen bolyongással analóg elvi modell. A véletlen bolyongás egyik változatában egy a bolyongó mozgását úgy írhatjuk le, mint ami minden lépés előtt feldob egy érmét, majd annak eredményétől függően egyet lép jobbra, illetve balra egy egydimenziós rács mentén. A kvantumos bolyongásban hasonló dolog történik, azonban mind a bolyongó, mind az érme kvantumosan viselkedik” – áll a Wigner Fizikai Kutatóintézet Qubitnek eljuttatott, a tanulmányt magyarázó anyagában.

A kvantumos bolyongó tehát egy hullámhoz hasonlóan, igen gyorsan szétterjed egyszerre több rácspontra. „Ha egy megfigyeléssel meg kívánjuk határozni a bolyongó helyzetét, akkor a bolyongó hirtelen lokalizálódik arra a rácspontra, ahol a jelenlétét érzékeljük. Ez értelmezhető úgy, hogy a mérés elpusztította a bolyongó kiterjedt állapotát. Azt, hogy a bolyongó a megfigyelés hatására melyik pontra fog lokalizálódni, a természet véletlenszerűen dönti el, és a kvantumelmélet matematikai leírása csupán arra ad lehetőséget, hogy ezeknek a véletlenszerű jelenségeknek a valószínűségét kiszámoljuk”.

„Mivel csupán közvetlen szomszédok közötti lépéseket tartalmaz, a kvantumos bolyongás viszonylag könnyen valósítható meg egy valós berendezésben. Ugyanakkor, mivel alkalmazások széles tárházát kínálja, fontos építőkövét alkotja különböző kvantumtechnológiai fejlesztéseknek” – írja az intézet.

Az MTA Wigner Fizikai Kutatóintézet kvantumoptikai és kvantuminformatikai osztályának munkatársai, Kiss Tamás és Gábris Aurél vezetésével az utóbbi 8 év során olyan kísérleti platform elméleti és gyakorlati alapjait dolgozták ki, amely a fényt felhasználva „kvantumos bolyongót szimulál összetett környezetben”.

A kísérlet

A platformot nem Budapesten, hanem a Paderborni Egyetemen készítették el a kutatók, Christine Silberhorn professzor és Igor Jex professzor vezetésével. „A németországi kísérletek során azt vizsgáltuk a szimulációs berendezésünkkel, hogya mérés milyen hatást gyakorol a kvantumos bolyongóra. Ám ahelyett, hogy az egyes lépések után a bolyongó konkrét helyzetére vonatkozó megfigyelést végeztünk volna, a kérdésünket arra szűkítettük, hogy a bolyongó vissza tért-e a arra a helyre ahonnét a bolyongását kezdte” – írják a kutatók. Mint kitérnek rá, ezt a kérdést a világhírű magyar matematikus Pólya György tanulmányozta elsőként még 1921-ben, ő vezette be a visszatérés matematikai fogalmát.

„A visszatérés ideális terep egy szimulációs eszköz megbízhatóságának értékelésére. A kísérleti munka során megközelítőleg 40 lépés hosszan szimuláltuk a kvantumos bolyongás folyamatát és megfigyelését mindkét módszer szerint. A visszatérésre vonatkozó eredmények közel tökéletes egyezést mutattak az elméletileg vártakkal. Egyéb kvantumelméletet használó protokollok kísérleti megvalósításaival való összehasonlításban, a 40 iteráció elvégzése után is túlnyomóan kvantumos viselkedés megfigyelése kiemelkedő eredmény” – állítják a magyar kutatók.

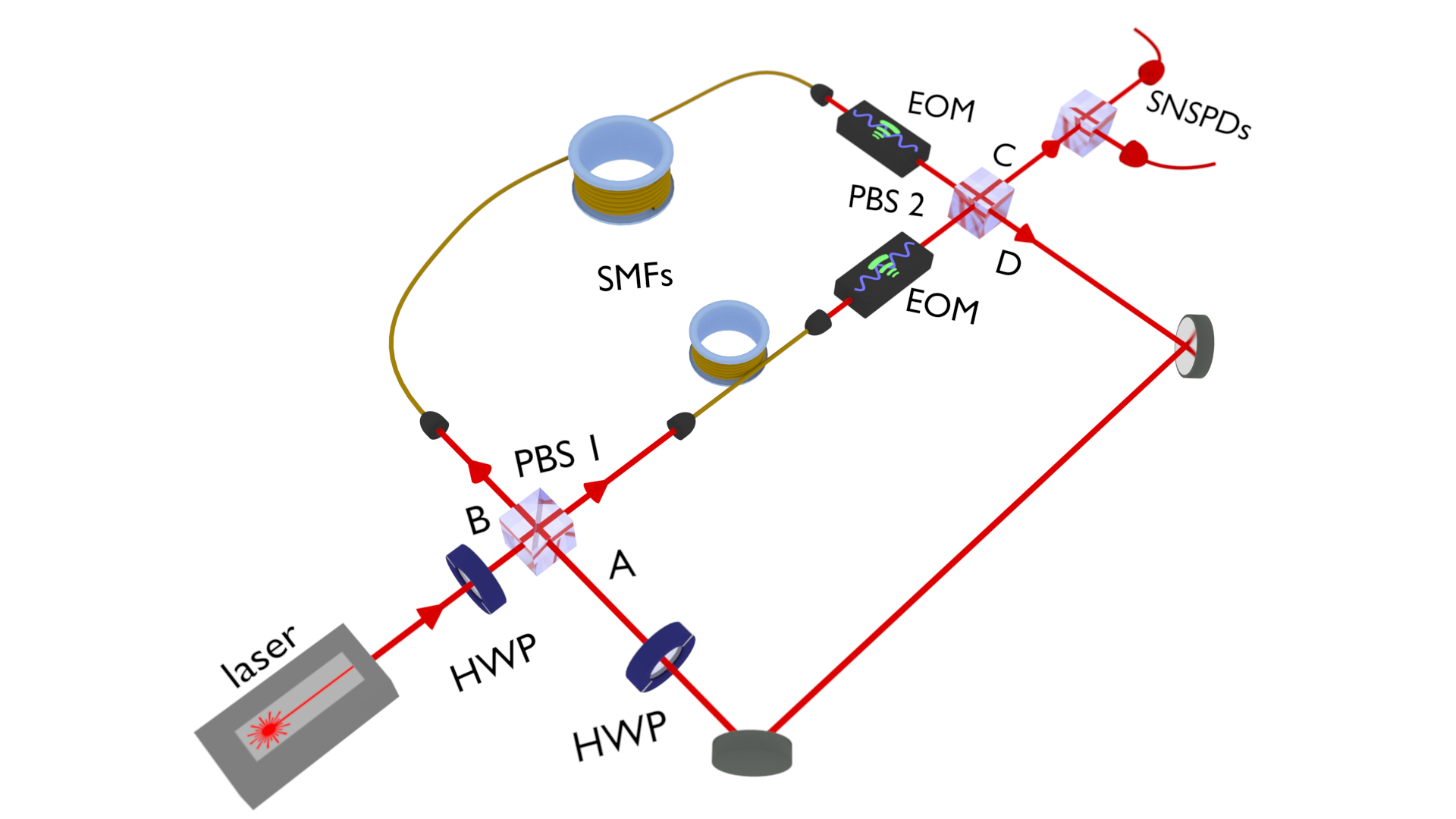
A tanulmány szerint a fénynek csupán a hullámos tulajdonságait használva sikerült megragadni a mérés egyedi kvantumos bolyongóra gyakorolt hatását. Ugyanakkor, figyelmeztetnek a kutatók, az analógia nem terjeszthető ki egynél több bolyongó esetére. „Ezért elsődleges jövőbeli célunk hogy kilépjünk a hagyományos fény birodalmából, és egyedi fotonok bolyongását figyelhessük meg. Mivel a platformot eleve úgy terveztük meg, hogy kompatibilis legyen egyedi fotonokat kibocsátó kvantumos fényforrásokkal, a fő kihívás ezen források alkalmazása a berendezésünkhöz. A téma távlati célja a mostani alapkísérletek nagy számú bolyongóra és hosszú időskálára való kiterjesztése. 10¹⁰ nagyságrend esetén például már biztosan találnánk praktikus alkalmazást is”.

Rockenbauer Antal elméleti fizikus, a Qubit állandó szerzője, a BME és az ELTE címzetes egyetemi tanára szerint a kutatócsoportok kitűnő munkát végeztek, és igen jelentősnek mondható, hogy egy új eszközt alkottak bizonyos kvantumhatások kimutatására. A kvantumtechnológiában új irányt jelenthet a bolyongási jelenség visszatérési mechanizmusának tanulmányozása. Rockenbauer ugyanakkor óvatosabb annak megítélésében, hogy valóban olyan egyszerű az úgynevezett koherens lézernyaláb helyett továbbvinni a kísérletet az egy-fotonos mérések irányába. „Szerintem ez nem csak annyit jelent, hogy a fényforrás intenzitását lecsökkentjük az egy-fotonos szintre, hiszen a jelenség kimutatásánál maximálisan el kell kerülni a termikus sugárzásból származó zavaró hatásokat” – válaszolt kérdésünkre az elméleti fizikus, aki szerint ennek kivitelezése még sok munkát kíván.