A parabolikus csillaggal kapcsolatban az volt a bizonyítandó, hogy a feketére színezett és fehéren hagyott részek összterülete ugyanakkora, ha a karokat páros sok részre osztottuk.

Azt fogjuk megmutatni, hogy tetszőleges két szomszédos kar közé eső részre igaz az állítás. Először is könnyítsünk a helyzetünkön és vegyük észre, hogy egy ilyen részt megfelelő nyújtásokkal derékszögűre és egyenlő karhosszúságúra tudunk transzformálni, miközben a területek aránya nem változik meg.

A transzformáció után kapott derékszögű negyedcsillag karokkal érintkező területelemeit osszuk fel háromszögekre a bal oldali ábrán látható módon, lásd alább. Mivel a karok páros részre voltak osztva, a kapott háromszögek párba állíthatók. A szomszédos sötét és világos kék háromszögek területe pedig megegyezik, mert alapjuk ugyanakkora – akárcsak a magasságuk, mivel az alappal szemközti csúcs közös. Hasonló módon megegyezik a szomszédos piros és narancs színű háromszögek területe.

A háromszögelés befele is tovább folytatható értelemszerűen, és ha belátható lenne, hogy a belsőbb háromszögek is párba állíthatók, és területük megegyezik, akkor azzal készen is lennénk. Ehhez azonban teljesülnie kéne, hogy a párba állított belső háromszögek alapjai is megegyeznek. A karok mentén ez azért teljesült, mert a karokat egyenlő részekre osztottuk fel, és ezek a részek éppen a szóban forgó háromszögek alapjai voltak. Egy bentebb lévő ferde vonalról azonban nem látszik automatikusan, hogy az őt keresztező többi ferde vonal egyenlő közönként metszené. Pedig így van, ezt fogjuk megmutatni.

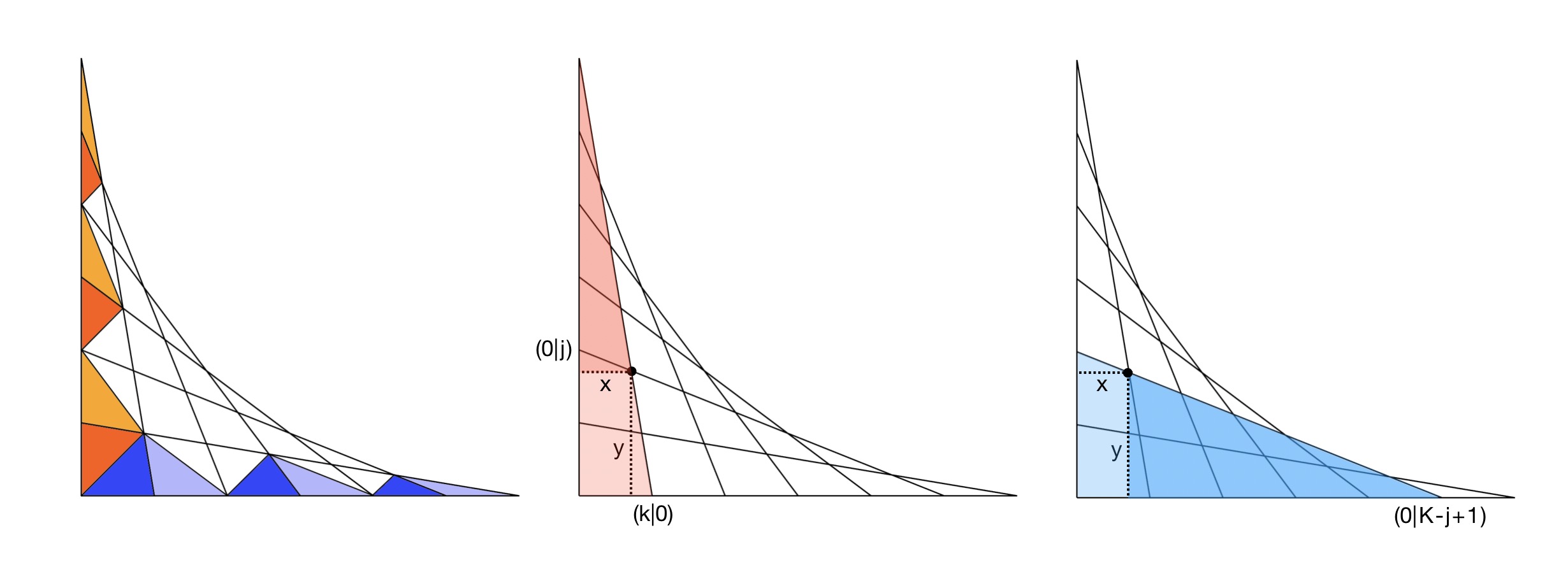
Ahhoz, hogy ezt belássuk, vegyünk két tetszőleges egymást metsző ferde vonalat. Az általánosság megkötése nélkül az egyik legyen a (0|j) koordinátájú pontból kiinduló, a másik pedig a (k|0) koordinátájú pontból kiinduló egyenes, lásd a középső ábrát. Az egységeket válasszuk úgy, hogy a karok mentén épp egységenként legyenek a beosztások, tehát j és k egész számok lehetnek 1-től K-ig, ahol K a karok osztásának száma. Ekkor a (0|j) koordinátájú pontból kiinduló egyenes az x-tengelyt a (K-j+1|0) pontban metszi, a (k|0) koordinátájú pontból induló pedig a (0|K-k+1) pontban végződik az y-tengelyen. Az ábrán lévő példában K = 6, j = 2, k = 1. A két ferde vonal metszéspontját egy fekete pont jelöli az ábrán, ennek koordinátái legyenek (x|y).

A középső ábrán bejelölt sötétebbik piros háromszög és az azt tartalmazó halvány piros háromszög egymáshoz hasonlóak, és ezt a hasonlóságot kihasználva felírható az alábbi arányossági összefüggés: (K-k+1-y) : (K-k+1) = x : k. Hasonlóan a jobb oldali ábrán bejelölt sötétkék háromszög és az azt tartalmazó halvány kék háromszög egymáshoz hasonló, ezért: (K-j+1-x) : (K-j+1) = y : j. Ezeket az egyenleteket természetesen csak akkor írhatjuk fel, ha van metszéspont. Amikor j = K-k+1, akkor a két egyenes éppen egybeesik és nem lesz metszéspont. Továbbá szimmetria okoból elegendő lesz csak a (K-k)-nál nem nagyobb j eseteket vizsgálni.

Mármost az első egyenletből x = k·(K-k+1-y)/(K-k+1), amit behelyettesíthetünk a másodikba, és y-ra megoldhatjuk. Ha azt találnánk, hogy y arányos j-vel, akkor készen lennénk, hiszen ha a k-val paraméterezett ferde vonalon a j. metszéspont távolsága az x-tengelytől j-vel arányos, akkor a metszéspontok egyenlő közönként következnek.

Az y változóra egy lineáris egyenletünk van, aminek a megoldása nem túl bonyolult, inkább az eredmény egyszerűsítése igényel némi számolást, hogy belássuk a j-vel való arányosságot. Az ilyen esetekben, amikor valaki látja, hogy mit kéne kiszámolni, de nem szeret számolni, nyugodtan használhat matematikai segédprogramot. A webes felülettel rendelkező WolframAlpha program például a segítségünkre lehet. Ha beírjuk neki, hogy "solve (K-j+1-k·(K-k+1-y)/(K-k+1))/(K-j+1) = y/j, y", akkor egy pillanat alatt kiírja nekünk a megoldást, mégpedig a lehető legegyszerűbb formában, tehát egyszerűsítéssel sem kell már bajlódnunk. Egyébként, ha nem ismerjük a szintaxist, a WolframAlpha akkor is megpróbálja kitalálni, hogy mire gondoltunk, és felajánl egy csomó lehetőséget magyarázatokkal együtt. A megoldás y = j·(K-k+1)/(K+1) lesz, vagy más formában y/j = 1-k/(K+1), vagyis y valóban arányos j-vel. Ellenőrzésképpen akár vissza is lehet helyettesíteni.

Végül még  néhány szó arról, hogy miért nevezik az ilyesmit parabolikus görbeseregnek. Természetesen azért, mert ha végtelenségig növeljük a karokon a felosztást, akkor a görbék burkolója egy parabola lesz. Akit bővebben érdekel, utánanézhet itt.