Felejtős memóriakártya című feladványunkban az volt a kérdés, hogy egy klasszikus párkereső memóriakártya-játékban milyen stratégia szerint és maximum hány párt kell megfordítanunk ahhoz, hogy megtaláljuk az összeillő párokat abban az esetben, ha nincsen vizuális memóriánk, vagyis nem emlékszünk arra, hogy milyen ábrák szerepeltek a korábban felfordított kártyákon. Csak arra emlékszünk, hogy mely pozíciókat (illetve párokat) fordítottuk már meg.

A megoldást Dévai Gergely, Tommy Singh és Boros Péter gondolatmenetei alapján állítottuk össze.

Legyen n pár, azaz 2n darab kártyalap a játékban. A következő két algoritmus mindegyike olyan, a legkedvezőtlenebb esetekben a fordítások száma n² lesz. A hivatkozhatóság kedvéért a kártyákat számozzuk meg 1-től 2n-ig.

1. algoritmus: Vegyük az 1. helyen álló kártyát, és hasonlítsuk össze rendre a tőle nagyobb sorszámú kártyákkal, amíg meg nem lesz a párja. Amikor megvan, kezdjük az eljárást újra a hátralevő kártyák közül a legkisebb sorszámúval. Legrosszabb esetben a fordítások száma: (2n-1) + (2n-3) + (2n-5) + ... + 5 + 3 + 1 = (2n-1+1)·(n/2) = n².

2. algoritmus: Vegyük a 2. helyen álló kártyát. Hasonlítsuk ezt össze rendre a nála kisebb sorszámúakkal, amik még az asztalon vannak. Egyezés esetén a párt levesszük, és újrakezdjük az egyel nagyobb sorszámú kártyával. Ha nem volt egyezés, akkor is ugyanígy az egyel nagyobb sorszámúra ugrunk. Ha eljutunk addig, hogy az első n kártya között már minden egyezést megnéztünk és nem találtunk párt, akkor az (n+1). sorszámú kártya esetében már biztos fogunk találni párt, ezért a legrosszabb esetben a fordítások száma: 1 + 2 + 3 + ... + (n-2) + (n-1) + n + (n-1) + (n-2) + ... + 3 + 2 + 1 = n·(n-1) + n  = n².

Arra is van egyébként lehetőség, hogy ezt a két algoritmust kombináljuk. Továbbá Boros Péter szimulációi alapján az derül ki, hogy az átlagosan szükséges fordítások száma is azonos a két algoritmusra, mégpedig n·(n+1)/2.

Láttuk tehát hogy több algoritmus is van, amivel legrosszabb esetben is n² fordítás elegendő. Azt fogjuk megmutatni, hogy ennyi tetszőleges algoritmus esetében is szükséges, ha nincsen szerencsénk. Ehhez előbb egy segédtételt látunk be.

Segédtétel: Ha egy 2n csúcsú gráfban pontosan egy teljes párosítás van, akkor a gráfnak maximum n² éle van. Teljes párosítás alatt azt értjük, hogy a gráf csúcsait összekötő élek közül ki tudunk választani n darabot úgy, hogy az azokhoz tartozó 2n csúcs mind különbözik egymástól, vagyis a gráf összes csúcsát párosítják ezek az élek.

Bizonyítás: Legyen a szóban forgó gráfnak m éle. Legyen a teljes párosítás (ábrán pirossal) egyik élének két végpontja v és w csúcsok. Legyen a v-ből kiinduló élek száma k. Mivel v-ből megy él w-be, ezért k legalább egy. Ha k > 1, akkor legyen p egy olyan w-től különböző csúcs, amibe megy él v-ből. Azt mondjuk erre, hogy p v-nek egy w-től különböző szomszédja a gráfban. Mivel p is része a teljes párosításnak, ezért van neki egy csúcspárja, legyen ez q, amivel él köti össze (fekete). Mármost w-ből nem mehet él q-ba (szürke szaggatott), mert akkor w-q-p-v-w egy 4-es ciklus lenne a gráfban, amin belül ennek a négy pontnak több párosítása is lehetséges volna: a v-w és p-q párosítás helyett a q-w és v-p párosítás is lehetséges volna, ami azt eredményezné, hogy a teljes párosítás sem lenne egyértelmű.

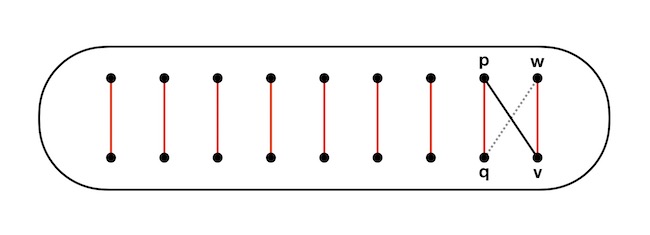
Amit elmondtunk v-nek egy w-től különböző szomszédjára, az v-nek bármelyik w-től különböző szomszédjára is igaz, amiből (k-1) darab van, és ezek egyikébe sem mehet él a w-ből. A w-ből kimenő élek száma tehát maximum (2n-1)-(k-1) lehet. A v-ből és w-ből kimenő élek számának összege pedig együttesen maximum k+(2n-1)-(k-1) = 2n. De ez igaz a teljes párosítás bármelyik élére, illetve annak végpontjaira. Ha az összes csúcsra összeadjuk a csúcsokból kimenő éleket, akkor mine élt kétszer számolunk, tehát azt kapjuk, hogy 2m ≤ n·2n, vagyis m maximum n² lehet. Q.E.D.

Térjünk most vissza az eredeti feladathoz. A csúcsoknak természetesen a kártyák fognak megfelelni. Van 2n csúcs között egy teljes párosítás, amit szeretnénk megtalálni. Egy kérdésnek nevezzük az, amikor két kártyát felfordítunk. Ilyenkor megtudjuk, hogy párban vannak-e vagy sem, vagyis van-e a kártyáknak megfelelő két csúcs között él, vagy biztosan nincsen. Tekinthetjük úgy, hogy kezdetben nem tudunk semmit, bármi bármivel párban lehet, ezért a teljes gráfból indulunk ki, amiben minden csúcs minden csúccsal össze van kötve, és amikor megtudjuk hogy valami nem pár, akkor a neki megfelelő élt kitöröljük a gráfból. 2n csúcs között összesen 2n·(2n-1)/2 = 2n² - n darab él lehetséges, amire rá lehet kérdezni.

Legrosszabb esetben úgy kérdezgetünk, hogy nem találunk sose párt, csak akkor, ha már elkerülhetetlen. Elkerülhetetlen alatt azt értjük, hogyha a kérdezett élt kitörölnénk a gráfból, akkor nem maradna teljes párosítás. Mármost, ha ebben az esetben n² -nél kevesebb kérdéssel megtalálnánk az összes párt, akkor a több mint 2n² - n - n² = n² - n meg nem kérdezett párral együtt az n pár összesen egy több mint n² élű gráfot alkotna, amiben a segédtételünk szerint több párosítás is létezne, akkor viszont mégsem volt elkerülhetetlen valamelyik elkerülhetetlen válasz, ami ellentmondás. Ezzel beláttuk, hogy legrosszabb esetben mégsem lehet n² -nél kevesebb kérdéssel megúszni.

A feladatra Dévai Gergely és Tommy Singh küldött be teljes megoldást. Közöttük sorsoljuk ki Szöllősi Péter GYÜMI Géniusz nevű vidám memóriafejlesztő kártyajátékát. A sorsoláshoz a jövő heti ötöslottó sorsolás számait fogjuk felhasználni. Ha a számok összege páratlan lesz a január 18-án esedékes sorsoláson, akkor Dévai Gergely, ha páros, akkor Tommy Singh lesz a nyertes.

Bónusz kérdés: mutassátok meg, hogy igazságos ez a sorsolási módszer.