Előző feladványunkban az volt a kérdés, hogy maximum hány olyan egybevágó alakzatot lehet megadni a gömb felszínén, amelyek mindegyike érinti az összes többit. Ugyanez megkérdezhető a síkon is. Síkon elhelyezhető például négy, amire egy nagyon egyszerű megoldás az alábbi. Vajon van ennél egyszerűbb is, olyan poligonokkal, amelyeknek az oldalszámuk ennél kevesebb?

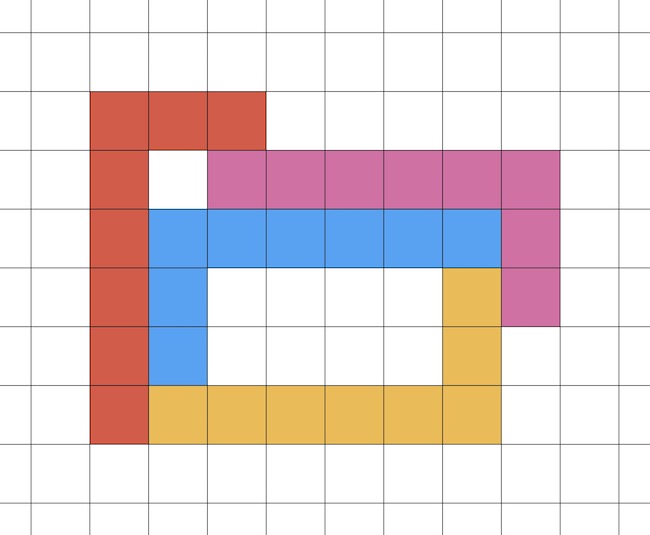
Vannak bonyolultabb megoldások is, mint például az alábbi hatszöges elrendezés.

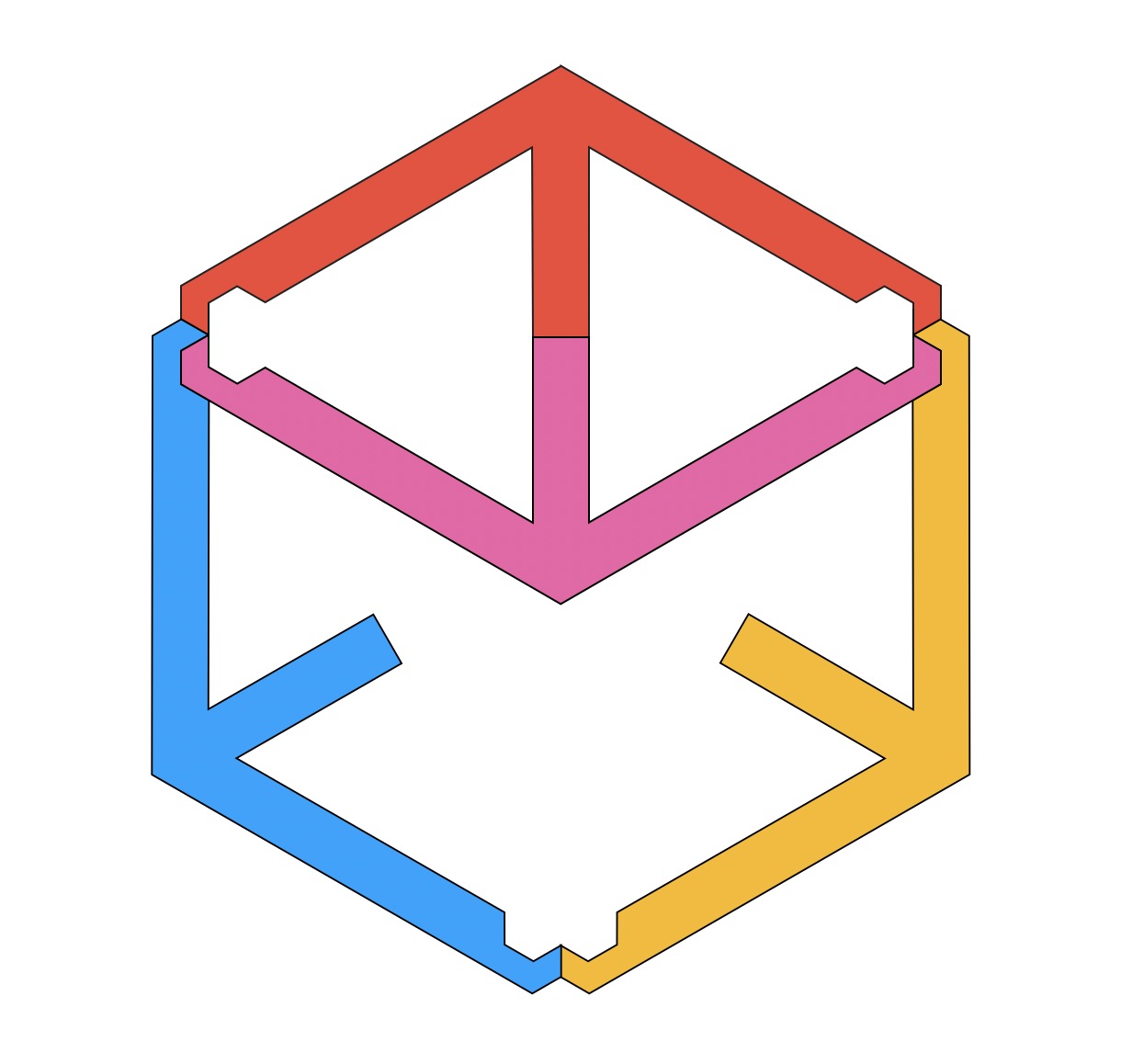
És olyan megoldást tudtok, amiben az alakzatok határvonalai csupa görbe vonalakból állnak össze, netán nincsenek is bennük csúcsok?

Az eheti feladvány azonban egy másik általánosítási lehetőségről szól. Síkidomok és felületdarabok helyett a térbeli testek világában keressünk hasonló konstrukciókat.

77. feladvány: Végtelen testi érintés

Meg lehet-e adni a térben tetszőlegesen sok külön-külön összefüggő, de egymással egybevágó testet, hogy azok mindegyike érintse az összes többit egy felület mentén?

Bónusz kérdés: Meg lehet-e adni végtelen sok ilyen testet egyszerre?

Nehézségi szint:

A megfejtéseket részletes indoklással és illusztrációkkal együtt az eszventura@qubit.hu címre várjuk. A legértékesebb megoldást küldő versenyzők felkerülnek az Ész Ventura dicsőségfalára, közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: március 10. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész.