Az ikerparadoxon és a görbe tükör: látszat és valóság
Menjünk el egy vidámparkba, és bámuljuk meg magunkat a görbe tükrökben! Ha homorú a tükör, sokkal vékonyabbak leszünk, míg a domború tükörben kövérebbnek látszunk. Persze nem mi változtunk meg, csak a rólunk tükrözött kép torzít. Kicsit bonyolultabb, de hasonló dolog történik, ha felülünk egy űrhajóra, amely a fénysebesség közelébe repít minket. A kabinban semmi szokatlant sem tapasztalunk, amikor egyenletes nagy sebességgel haladunk, mert nem változik meg mozgásunk, súlyunk, és a kabin tárgyai is olyanok, mint induláskor.
De ha kinézünk az ablakon, a csillagvilág képe teljesen megváltozik. Nézzünk előre, és azt látjuk, hogy az előttünk lévő csillagok fénye kékebben világit, és sokkal közelebb került hozzánk. Nézzünk hátrafelé is: onnan már vörösebben fénylenek a csillagok, és meglepő módom, bár távolodunk, mégis az égi objektumok közelebb látszanak, mint indulásunk előtt. Mi történt? Hirtelen megváltozott a világ körülöttünk, vagy csak saját szemünk csap be minket? A nagy sebesség miatt olyan a látvány, mint ha görbe tükörbe néznénk. Persze ez már igazán szédítő tempó, a Földhöz képesti sebességünk közelít a fény 300 000 km/s-os értékéhez - legyen mondjuk annak 99,5 százaléka, azaz 298 500 km/s. Ezt persze mi aligha élhetjük meg, de az elemi részecskék igen, például a felső sztratoszférából érkező müonok, amelyeket a kozmikus sugárzás nagy energiájú protonjai hoznak létre, amikor ott fent ütköznek a levegő molekuláival. Ennél a sebességnél a relativitáselmélet Lorentz-kontrakciós szabálya szerint a távolságok tizedükre rövidülnek, amit a γ paraméter ad meg:
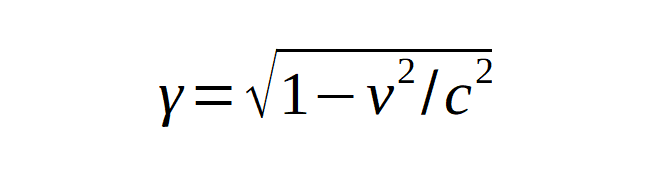
Ugyanekkora mértékben csökken a célba érés ideje is. Hogyan élik ezt meg a müonok, amelyek 15 km magasságban jönnek létre? Az ő életük rövidre szabott, amikor a födi laboratóriumban képződnek: felezési idejük 2,2 μs. Ez azt jelenti, hogy ennyi idő alatt számuk már felére csökken, és ez a feleződés exponenciálisan folytatódik. A fénynek is 50 μs időre van szüksége, hogy abból a magasságból eljusson a Föld felszínére, ezért azt várnánk, hogy a földi laboratóriumokban alig figyelhetnénk meg müonokat. Összevetve azonban a sztratoszférában képződő müonok számát a felszínen megfigyelt mennyiséggel, a mérések azt mutatják, hogy a száguldó müonok élettartama tízszer hosszabb lett. Ezt persze mi mondjuk saját koordinátarendszerünkben, a müonok viszont úgy „érzik”, hogy továbbra is 2,2 μs alatt feleződnek, csakhogy nekik 1,5 km volt a megtett útjuk a Lorentz-kontrakció miatt, és ehhez elég volt nekik 5 μs. Kétféle rendszerben gondolkozhatunk: a sajátunkban, itt a Földön állva, és a müon száguldó rendszerében. A relativitáselmélet szerint mind a kettő ekvivalens inerciarendszer, érvényesül bennük a fénysebesség állandósági szabálya, és ehhez kapcsolódóan azonos marad minden fizikai törvény.
Ikernek iker, de miért paradoxon?
Amikor az ikerparadoxonról beszélünk, mégis zavarba jövünk. Az ikerparadoxon akkor lép fel, ha összekötjük egymással az inerciarendszereket. Az ikrek egyike itt marad a Földön, a másik űrutazásra indul. Az egyszerűség kedvéért ne foglalkozzunk avval a szakasszal, amíg felgyorsul az űrhajó, és nézzük csak azt, amikor már nagy sebességgel, egyenletesen halad, azaz jogosan beszélünk inerciarendszerről. Ezt az indokolja, hogy az elvégzett kísérletek szerint a müon élettartama szempontjából nem számít, hogy mekkora volt a gyorsulás, amikor laboratóriumokban gyorsították fel a müonokat. Ha az űrhajó egy 10 fényévnyi körutat az 5 fényév távolságban lévő csillagig γ= 10 Lorentz-faktornak megfelelő sebességgel tesz meg, akkor ez számára csak 1 évet vesz igénybe, ha a gyorsulási és lassulási szakaszoktól most eltekintünk. A földi ikerhez képest így az űrutas 9 évet nyert, ami már érzékelhető korkülönbség az ikrek között.
Miért beszélünk paradoxonról? Ez a két inerciarendszer ekvivalenciájából következik! Az otthon maradó iker szempontjából a hozzá képest nagy sebességgel haladó testvérének órája lassabban ketyeg a nagy γ érték miatt, ezért az ő szempontjából a hazatérő iker lesz a fiatalabb. De hogyan fest a helyzet az utazó iker rendszeréből nézve? Ő is a saját rendszeréhez hasonlítja az ikertestvér sebességét, hiszen a relativitás elve miatt nincs abszolút sebesség, csak az számít, hogy mekkora a különbség a két inerciarendszer sebessége között. Ez ugyan negatív a földi rendszerből indított űrhajó sebességéhez képest, de mivel a sebesség előjele közömbös a γ Lorentz-kontrakció számításánál, így szerinte a Földön maradó ikertestvér órája lassul le a tizedére, tehát a találkozáskor az ikerpár másik tagja lesz a fiatalabb. Nyilvánvaló az ellentmondás a két gondolkozás között.
Kinek van igaza? Melyik állandó sebességű inerciarendszer alapján kell számolni? Talán mégis lenne egy abszolút vonatkoztatási rendszer, amiben az űrhajó sebessége a nagyobb?
Ha ezt nem akarjuk elfogadni, akkor csak arra gondolhatunk, hogy a két inerciarendszer mégsem ekvivalens: a számítás csak az egyikben ad helyes eredményt. De milyen alapon választjuk ki a helyes rendszert? A szokásos magyarázat a gyorsulásra hivatkozik, mondván: az utazó iker gyorsult és lassult, míg a másik helyben maradt, és ez aszimmetrikus előélet okozza a különbséget. Ezt magyarázza hosszasan a Wikipedia angol nyelvű szócikke is, ahol olyan számításokat végeznek el, amelyekben csak a gyorsulásról és lassulásról esik szó, és nem tárgyalják az állandó sebességű szakaszt. De ha a gyorsulás-lassulás a lényeg, akkor miért jön létre korkülönbség az egyenletes sebességű szakaszban, mégpedig arányosan azzal, hogy milyen hosszú ideig volt a két rendszer sebessége különböző? A müon példája is arra mutat, hogy nem számít a tényleges gyorsulás nagysága: a valódi magyarázatot az energiaátadás iránya adja meg.
A Föld teljes energiaállománya is kevés lenne
Induljunk ki az állónak tekintett földi rendszerből, amihez hozzávesszük a kozmikus sugarakat is. Ebből leválasztunk egy rendszert, például a levegő egy molekuláját, ami majd a müon forrása lesz a nagy energiájú protonnal ütközve, vagy az indulásra kész űrhajót, amit alaposan feltöltünk üzemanyaggal. Hogyan jön létre a Földtől leválasztott másik rendszer? Úgy, hogy a müon felhasználja a kozmikus sugárzás energiáját, az űrhajó pedig a földi rendszerből származó üzemanyagot. Tehát a nagy rendszer energiát ad át a részrendszernek, amelynek ezáltal sokszorosan megnő az energiája az eredeti mc2 nyugalmi energiához képest: esetünkben a megnövekedett energia az eredeti tízszerese lesz. Ez az energiafelvétel könnyen megvalósul a müon keletkezésekor annak parányi tömege miatt, de az űrhajó esetén ekkora energiát felvenni gyakorlatilag lehetetlen, annak hatalmas mennyisége miatt. Még ha fúziós energiát használunk is, mondjuk az üzemanyag nyugalmi energiájának 1 százalékát, az üzemanyag tömege az űrhajó tömegének ezerszerese lesz. Ha pedig nem egyetlen kilövéssel gyorsítjuk fel az űrhajót, hanem fokozatosan, rakétatechnikával, akkor még a fel nem használt üzemanyag gyorsítására is biztosítani kell energiát. Könnyű belátni, hogy ennek megvalósításához a Föld teljes energiaállománya is kevés. De lépjünk túl ezen a problémán, és koncentráljunk az elvi kérdésre: mit jelent az űrhajóra vagy a müonra nézve, hogy a nyugalmi energia tízszeresére tesz szert a felgyorsítás után? Az E = mc2 elv értelmében ez az eredeti tömeg tízszeres növekedésének felel meg. Ezt a tömegnövekedést viszont az űrhajósok nem érzékelik, mert ott minden fizikai folyamat a tömeg arányában lassul, legyen szó az atomfizikai vagy kémia reakciókról, illetve biológiai folyamatokról. A kicsi, a nagy, a lassú és a gyors vagy a könnyű és nehéz mind relatív fogalom, amit hétköznapi tapasztalataink hoznak létre, de az arányok mérésén alapul a fizika is, ezért ha világunkban minden arányosan változik, azt észre sem fogjuk venni. Ez történik a nagy sebességű űrhajóban is, ahol más lesz az egysége a tömegnek, az időnek és a távolságnak, de mivel ott minden arányosan változik, az űrhajós számára a változás nem lesz észrevehető. A látszat és valóság dilemmájával találkozunk: az csak a látszat világa, hogy a nagy sebességű űrhajóban közelebb kerültek hozzánk a csillagok. A valóság ezzel szemben az, hogy mi lettünk nagyobbak: megnyúlt a méterrúd, és annak hosszában mérve látszanak közelebb hozzánk a csillagok. Nem gondolunk arra, hogy az űrhajóban nagyobb lett minden méret, hogy lassabban ketyeg az óra, vagy hogy minden tárgy és magunk is nagyobb tömeggel rendelkezünk. Azt hisszük, hogy az űrhajó világában minden ugyanolyan maradt, mint amikor elindultunk a Földről.
Különös csavar ez a látszat és valóság között, mert az induló rendszerhez képest bekövetkező változás – amit egyébként látszatnak tekintünk – lesz a valóság, ami viszont az űrhajó belsejében rejtve marad előttünk. Csak akkor derül ki, hogy mi változott meg, ha kilépünk ebből a világból, és visszatérünk a Földre. Hasonló a helyzet a müon számára is: saját órája 5 μs időt mutat, amikor a sztratoszférából a földre ér, mert lassabban járt a mutató, pedig valójában 50 μs telt el keletkezése óta.
Fiatalabbak nem lehetünk, csak kevésbé idősek
A lényeg tehát az energiamérleg. Ez dönti el, hogy vajon a müon, illetve a száguldó űrhajó rendszerét kell-e alapul venni a számításokban, vagy a földi rendszert. Ha az űrhajó rendszeréhez viszonyítjuk saját sebességünket, azt nullának vesszük, amihez nem tartozik kinetikus energia. Viszont ebben a rendszerben a Föld fog közel fénysebességgel mozogni, amelynek kinetikus energiáját kiszámítva óriási értéket kapunk. De ez csak számítás, fikció, hiszen mitől nőtt volna meg a Föld mozgási energiája? Az energiacsere iránya nem válaszható meg önkényesen, nagyon is valóságosan kell befektetnünk rengeteg energiát a gyorsításhoz. Szintén valóságos folyamat, ahogy a kozmikus sugárzás protonja átalakítja a levegőmolekulát, és nagy sebességet ad a kirepülő müonnak. Az inerciarendszereket az energiaátadás iránya különbözteti meg. Az ekvivalencia csak egy matematikai, transzformációs szabály, amely kimondja, hogy a leírás szempontjából nincs különbség a két rendszer között: mindkettőben azonosak a fizikai törvényeink, de ez csak addig igaz, amíg fizikailag nem teremtünk kapcsolatot a két különböző sebességű rendszer között; amíg nem gondolunk arra, hogy honnan is származik a mozgó rendszer energiája. Általánosságban ugyan nem létezik kitüntetett referenciarendszer, de az energiával feltöltött rendszer számára kitüntetett szerepet játszik az a rendszer, ahonnan az energia érkezett.
Amikor az ikertestvér visszatér a hosszú útról, visszaadja a korábban felvett energiát, hiszen a Földhöz képest ekkor már nem mozog. Az ikrek korának összehasonlítása megkívánja, hogy előtte az űrhajó visszaadja környezetének a korábban felvett energiát. Az ikrek közötti korkülönbség fejezi ki a rendszer „emlékezetét” arra a körülményre, hogy a felgyorsított rendszer milyen hosszú ideig volt energiával feltöltött állapotban.
A legfontosabb megállapítás, hogy a matematikai ekvivalencia nem jelent egyúttal fizikai egyenértékűséget is, ennek hiánya viszont csak tényleges összehasonlításkor derül ki. A dilemma oka, hogy a Lorentz-kontrakció a sebesség négyzetével arányos. Ehhez kapcsolódik az idő irányának megfordítása is. Ha visszamennénk a múltba, a sebesség előjele megfordulna, de a négyzete azonos marad. Emiatt ugyan az időben előre vagy visszafelé haladás matematikailag ekvivalens művelet, az idő iránya mégsem fordítható meg, amit a fizika a termodinamikai entrópia törvényével magyaráz. Az idő megfordíthatatlansága tükröződik az ikerparadoxonban is: fiatalabbak nem lehetünk, csak kevésbé idősek. És persze azért sem irigyelhetjük az űrutast, mert bár naptári években számolva tovább élhet, a hosszú út alatt megtakarított idő egyúttal azt jelenti, hogy kevesebb élményhez jutott, mint ha itt maradt volna a Földön.
A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára. A Kalandozások a fizikában címen a Qubiten futó sorozatának korábbi írásai itt, tudósportréi pedig itt találhatók.
Kapcsolódó cikkek a Qubiten: