A Balaton partján a homokban 12 egész kagylónak a két fele, azaz 24 darab kagylóhéj található külön-külön szétszóródva. Ezekből hat gyerek mindegyike 4 fél kagylót gyűjtött össze, de egyikük sem talált párt. Együtt mind a 24 felet összeszedték. 97. feladványunkban az alábbi kérdéseket tettük fel.

1. kérdés: Előfordulhat-e az, hogy hiába választhatok mindegyik gyerektől egy fél kagylót, mégsem tudok összekunyerálni három összetartozó párt?

2. kérdés: Mi a helyzet akkor, ha 15 pár van a homokban, és a hat gyerek mindegyike 5-5 kagylót gyűjtött, de most sincs senkinél pár? Igaz-e, hogy ilyenkor mindig össze lehet kunyerálni három összetartozó párt, ha mindenkitől választhatunk egy tetszőleges fél kagylót?

3. kérdés: Most 50 kagyló van (azaz 100 fél darab) és 10 gyerek mindegyike 10 felet gyűjtött, de senkinél nincs pár. 5 összetartozó felet össze tudunk-e biztosan kunyerálni?

Figyelem: Ha valaki szeretné megoldani ezeket a feladványokat, ne görgessen tovább!

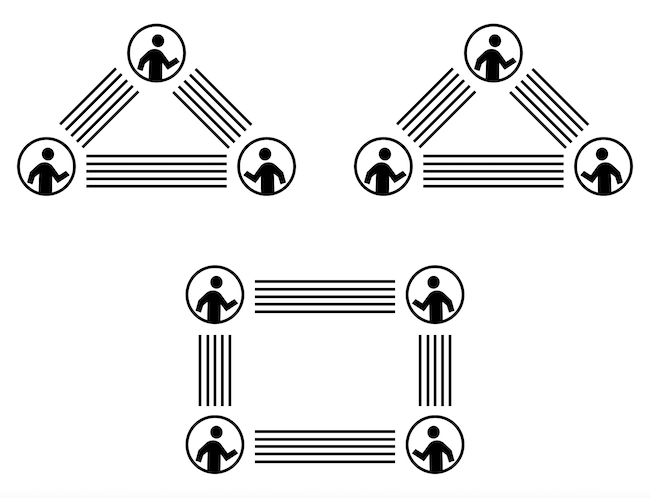
Az első esetben előfordulhat, hogy nem tudunk összekunyerálni 3 párt, erre mutatunk alább egy példát. Az alábbi ábrán a körök (6 db) a gyerekek, a vonalak (12 db) pedig az összetartozó félkagylókat kötik össze. Ha egy vonal egyik vége egy gyereknél van, akkor a szóban forgó gyerek birtokolja a vonal által reprezentált kagyló egyik felét. Minden körtől 4 vonal indul ki, tehát teljesül, hogy minden gyereknél 4 félkagyló van. Senkinél nincsen pár, azaz a vonalak mindig két különböző gyereket, azaz kört kötnek össze.

Ugye mindenkinek a multigráfok ugrottak be rögtön?

A fenti konstrukcióra tekinthetünk úgy is, mint egy multigráfra, amiben a gyerekek a csúcsok. A multigráf olyan gráf, amiben megengedettek a többszörös élek, és akár a hurokélek is. Ez utóbbi azonban itt nincs, mert az éppen azt jelentené, hogy valakinél pár van, amit kizártunk.

Láthatjuk, hogy a konstrukciónkban a multigráf két komponensre esik szét. Ha tehát 2 gyerektől elkérek egy-egy összetartozó félkagylót, akkor a velük egy klaszterbe tartozó harmadik gyerektől már csak olyan félkagylót kérhetek, aminek a párja az iménti két gyereknél van. De egy gyerektől csak egy fél kagylót kérhetek, tehát a fenti esetben nem tudok 3 összetartozó párt összekunyerálni.

Ha gráfelméleti nyelven szeretnénk a fenti feladatot tömören megfogalmazni, akkor így hangzott volna a kérdés, ahogy arra Endrey Márk megoldónk felhívta a figyelmet: Igaz-e, hogy minden lehetséges 6 csúcsú 4-reguláris hurokélmentes multigráfnak van független lefedő élhalmaza? A 4-reguláris azt jelenti, hogy minden csúcs fokszáma 4, tehát mindenki 4 félkagylót talált. Független élek alatt pedig olyan éleket értünk, amiknek nincs közös csúcsuk. A válasz a kérdésre: nem, hiszen mutattunk egy ellenpéldát, egy olyan 6 csúcsú 4-reguláris hurokélmentes multigráfot, amelynek nincs független lefedő élhalmaza, azaz nincs 3 olyan él a fenti multigráfban, amik végpontjai mind a 6 csúcsot tartalmazzák, azaz lefedik.

Most nézzük a 3. kérdést, ami most így fogalmazható meg: igaz-e, hogy minden lehetséges 10 csúcsú 5-reguláris hurokélmentes multigráfnak van független lefedő élhalmaza? A válasz szintén nem, vagyis mutatunk olyan 10 csúcsú 10-reguláris hurokélmentes multigráfot, amelynek nincs független lefedő élhalmaza. Az alábbi multigráfnak 3+3+4 = 10 csúcsa van, minden csúcsból 5+5 = 10 él megy ki, összesen pedig 50 éle van a gráfnak, de a két független többszörös háromszög miatt most sem lehet független élekkel (5 darabbal) lefedni az összes csúcsot.

Dupla indirekt bizonyítás

Legvégül nézzük a 2. kérdést, ez lesz a legnehezebb, mert itt nem tudnánk ellenpéldát mutatni, tehát bizonyítást kell adnunk arra, hogy mindig össze tudunk kunyerálni 3 összetartozó párt. Dévai Gergely megoldónk gondolatmenetét fogjuk követni. Feltesszük, hogy van egy a feladat feltételeinek megfelelő 6 csúcsú 5-reguláris hurokélmentes multigráfunk, de nem tudunk 3 független élt választani, és ebből próbálunk ellentmondásra jutni.

Válasszuk ki a multigráfnak egy tetszőleges élét, és távolítsuk el a multigráfból az él két végpontját (nevezzük A-nak és B-nek) és a belőlük kimenő összes élt is. Ekkor a maradék 4 csúcsú gráfban nem lehet két független él. Ennek a maradék gráfnak legalább 6 éle van, mert az eredeti 15 élből legfeljebb 1+4+4 = 9 élt vehettünk el.

Most azt állítjuk, ha ebben a 4 csúcsú és legalább 6 élű multigráfban nincs 2 független él, akkor van egy olyan csúcs, amiből nem indul ki él. Ennek a segédtételnek a bizonyítása szintén indirekten történik: feltesszük, hogy van egy olyan elrendezés, ahol minden csúcsnak van éle, mégsincs két független, és ebből ellentmondásra fogunk jutni, amiből következik majd, hogy nem lehetséges az, hogy minden csúcsból indul ki él.

Vegyünk egy élet a 4 csúcsú részgráfban, legyen a két végpontja C és D. A maradék két csúcs legyen E és F, köztük nem lehet él. Tehát E és F élei mind C-ben vagy D-ben végződnek. Ha viszont valamelyikből C-be és D-be is megy él, az nem jó, mert akkor a másikból akár C-be, akár D-be megy él, azzal már lesz két független. De az sem jó, ha az egyikből C-be, a másikból D-be mennek az élek, mert ezek is függetlenek. Vagyis E-ből és F-ből minden él egyetlen csúcsban (vagy C-ben vagy D-ben) végződik. Ekkor viszont ez egy 6 fokú csúcs lenne (a C és D között menő élet is beleszámolva), ami ellentmond a feltételeknek.

Arra jutottunk tehát, hogy kell lennie egy él nélküli csúcsnak a C, D, E, F között, nevezzük ezt C-nek. Ekkor az eredeti, 6 csúcsú multigráfban C minden éle A-ban vagy B-ben végződik. Nem végződhet mind ugyanabban, mert akkor az A és B között menő éllel együtt túllépnénk az 5-ös fokszámot. Ebből tehát az következik, hogy van él C és A között és C és B között is.

Az eredeti, 6 csúcsú gráfban minden csúcs 5 fokú ezért a D, E, F csúcsoknál összesen 3×5 élvégződés van, és mivel ez páratlan, ezért nem végződhet mindegyik a D, E, F háromszögön belül. C felé nem mehet, vagyis lesz él ebből a háromszögből A vagy B felé. Az általánosság megszorítása nélkül feltehetjük, hogy A felé van kimenő él. Ugyanakkor C és B között is van él, tehát ezt eltávolítva újra alkalmazhatjuk a korábbi segédtételt, vagyis az A, D, E, F részgráfban is kellene lenni egy él nélküli csúcsnak. Ez azonban nem lehet, mert a D, E és F csúcsok össze vannak kötve, hiszen a köztük menő legalább 6 él nem mehet csak két csúcs között (az 5-regularitás miatt), tehát a háromszög mindegyik csúcsából megy ki él, viszont A-ból is megy él valamelyikükbe. Így tehát ellentmondásra jutottunk. Q. E. D.

Kapcsolódó cikk a Qubiten:

link Forrás