Ész Ventura: A Pitagorasz-tétel segít a fenyőket a csillagba zsúfolni

Karácsonyi szuszakolós feladványainkban, a 106. és 107. feladványban, egy hatágú csillagba kellett minél több fenyőfát átfedés- és kilógásmentesen elhelyezni.
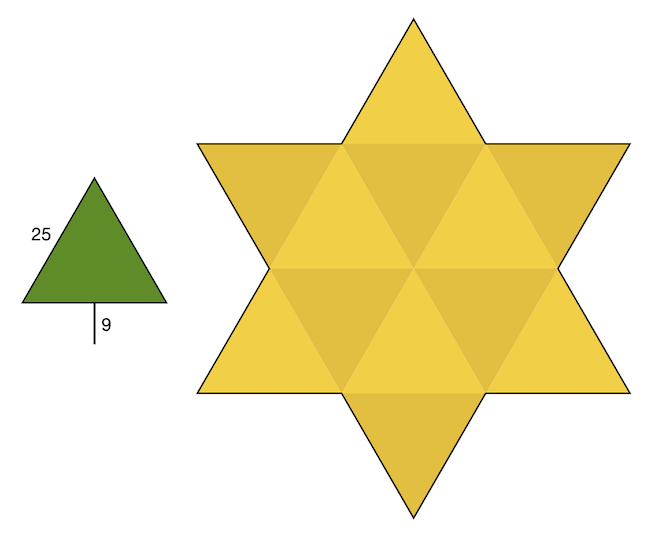
Az első szuszakolós feladatnál a háromszögek oldalhossza 25, a fenyő szára pedig 9 centiméter volt. Az aranyszínű, szabályos háromszögekből álló, csillag alakú területen kellett nyolc darab fenyőfát elhelyezni úgy, hogy ne fedjék egymást, se a koronájuk, se a száruk. A fenyőket szabad volt forgatni, a szárukról pedig feltettük, hogy elhanyagolható a vastagságuk.
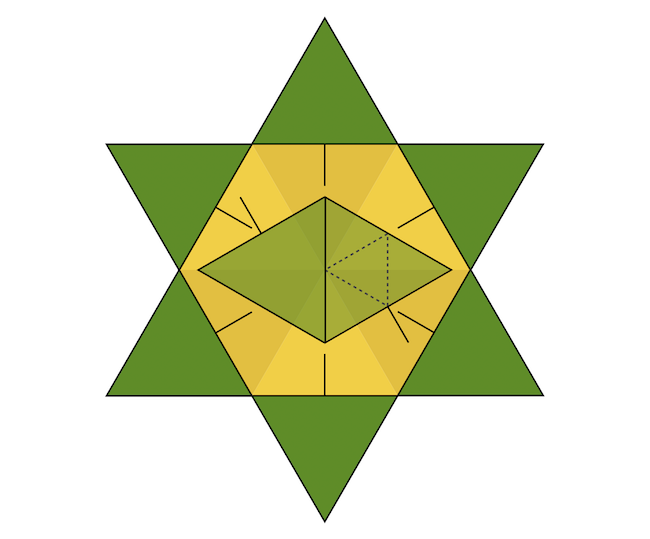
Alább látható egy lehetséges megoldás, ahol a fenyők szárát egy picit rövidebbre rajzoltuk a jobb láthatóság kedvéért. A valóságban vonalvastagságon belül lenne a különbség, de épp nem érnek egymáshoz. Ennek belátásához elég egy Pitagorasz-tétel, amivel egy fenyő koronájának, azaz egy szabályos háromszögnek a magasságát kiszámoljuk, ez körülbelül 21,65 centiméter. Ha ebből levonjuk a 9 cenitmétert, akkor marad 12,65 cm, ami nagyobb a szabályos háromszög fél oldalhosszánál, tehát a csillag ágaiban lévő fenyőfák befelé forduló szárai nem fognak hozzáérni a belső fenyőfákhoz.
Ennek illusztrálására szaggatott vonallal berajzolunk a jobb oldali belső fenyőfa koronájába a korona oldalfelező pontjai által alkotott, fele akkora oldalhosszú szabályos háromszöget, amelynek egyik oldala épp egy egyenesbe esik az egyik külső fenyő befele forduló szárával. Természetesen még azt is be kell látni, hogy a belső fenyőfák szára sem éri el a külső fák koronáját, ami talán még könnyebb – ezt már az olvasókra bízzuk.
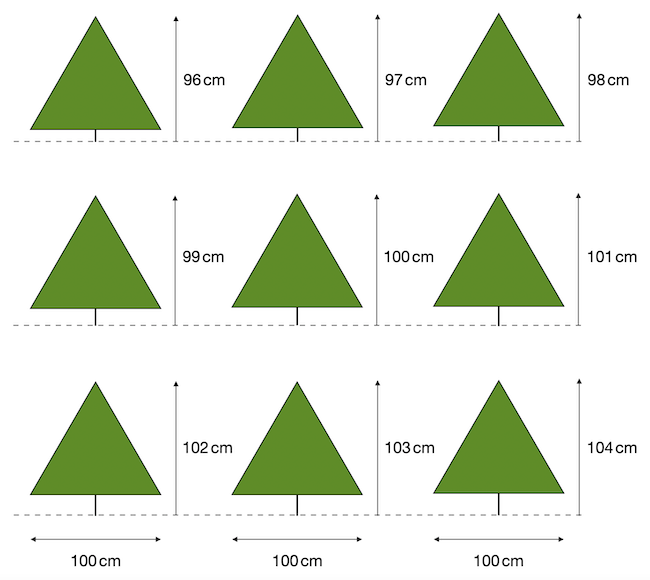
A második szuszakolós feladatnál kilenc fenyőfát kellett szintén egy csillagba pakolni, amelyeknek a lombkoronái egyformák, száruk azonban eltérő hosszúságú volt. A fenyők magasságai rendre: 96, 97, 98, 99, 100, 101, 102, 103 és 104 centiméter voltak, lásd az alábbi ábrát.
A csillagot alkotó háromszögek szintén megegyeznek a lombkoronák méretével, a háromszögek oldalhossza most azonban 100 centiméter. Egy lehetséges megoldást mutat az alábbi elrendezés, ahol a fák magasságait beírtuk a lombkoronába.
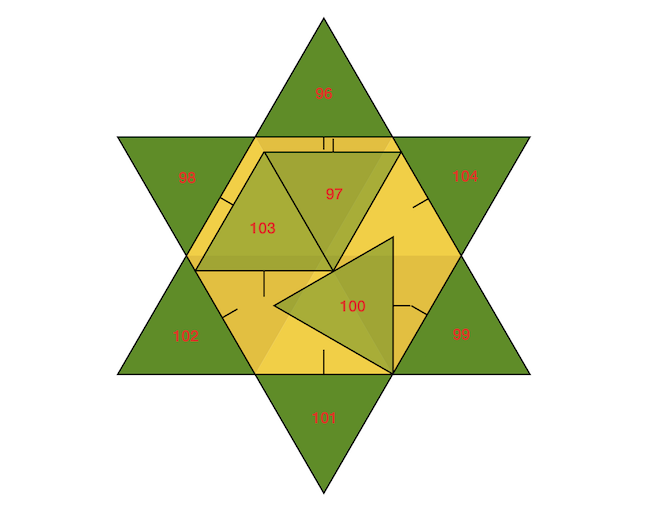
Annak belátásához, hogy a szárak nem metszik egymást, megint csak nem kell több, mint néhány Pitagorasz-tétel, amit a kedves olvasókra bízunk.
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész.
Kapcsolódó cikkek a Qubiten:
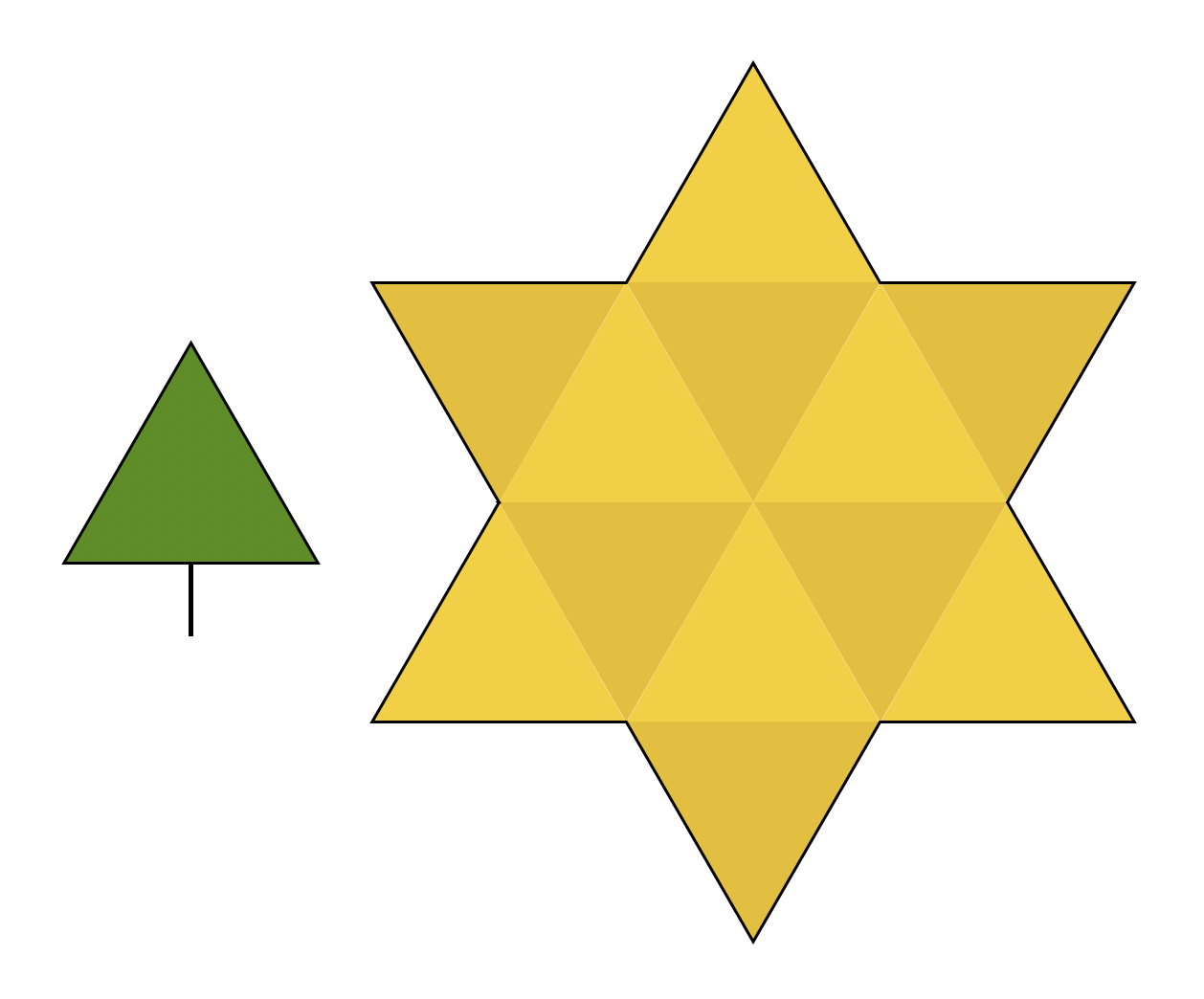
Ész Ventura: Be tudsz szuszakolni nyolc fenyőfát ebbe az aranyszínű csillagba?
A feladat, mint minden karácsonykor, hogy a fát beszuszakoljuk, csak ezúttal nem talpba, hanem egy hatágú csillagba, ráadásul nyolc darabot. Az ábrán látható szabályos háromszögek mind egyformák, oldaluk 25 cm. A fenyő szára 9 cm. Menni fog?

Ész Ventura: Kilenc fenyőfát is be tudsz szuszakolni egy csillagba?
Előző heti feladványunkban nyolc egyforma fenyőfát kellett a hatágú csillagba szuszakolni, most kilencet kellene, de a száruk eltérő hosszúságú. Ez is menni fog?