175. feladvány: Négyzet négyzetrácson

Egy négyzetrácsos lapra az alábbi rácssokszöget rajzoltuk. Az ábrát kiegészíthetjük még nyolc, egységnyi hosszúságú vonallal, de ezek csak a négyzetrács vonalain haladhatnak. A végső ábrának összefüggőnek kell lennie, azaz a megrajzolt vonalak mentén bármely pontjából bármely másik pontjába el kell tudni jutni. Lehetséges-e úgy bővíteni a lenti alakzatot, hogy a végső ábra tartalmazza egy olyan négyzetnek a négy csúcsát, amely négyzet oldalhossza öt egységnyi? Az egység a négyzetrácsot alkotó legkisebb négyzetek oldalhossza.

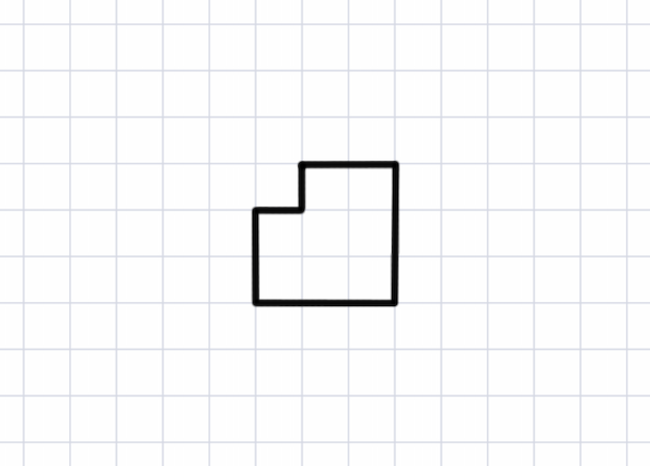
Bónusz kérdés: Ha van megoldás, akkor hány különböző megoldás van?

Nehézségi szint:

A megfejtéseket részletes magyarázattal és a szükséges ábrákkal együtt az eszventura@qubit.hucímre várjuk. A leggyorsabb és legkreatívabb megoldást küldő versenyzőink felkerülnek az Ész Ventura dicsőségfalára – közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. A versenyről minden tudnivaló megtalálható: itt. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: május 10. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.