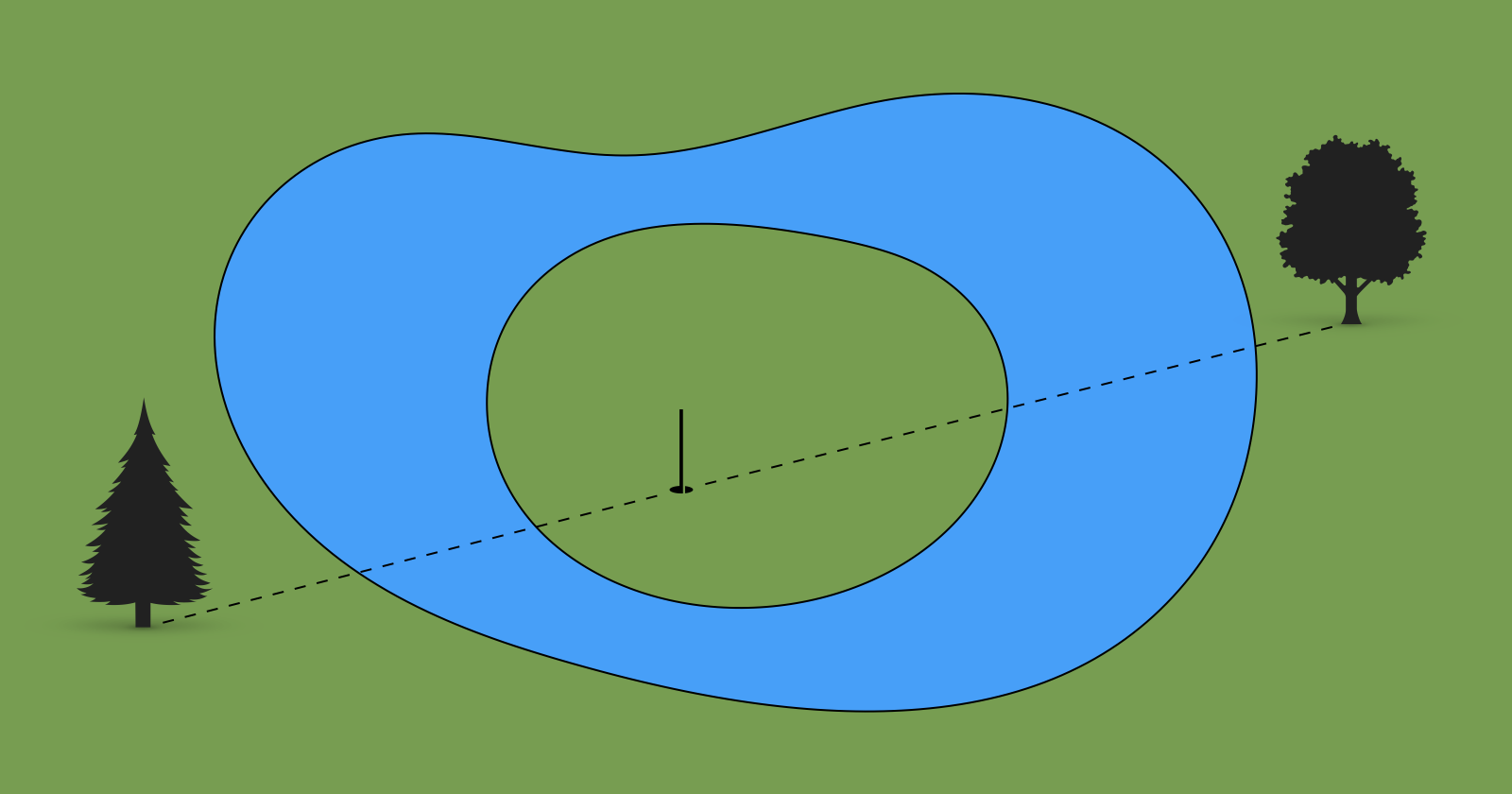
Köteles mérés egy szigeten című feladványunk nagyon népszerű volt, sokak fantáziáját megmozgatta. A feladat szerint egy üres szigeten vagyunk, és nincsen semmi másunk, csak egy csomó kötelünk és karónk. A tavon túl a tó két átellenes oldalán két fa magasodik, és az a feladat, hogy a sziget elhagyása nélkül mérjük meg a fák közötti távolságot, vagyis mérjünk ki a szóban forgó távolságnak megfelelő hosszúságú kötelet. A kötelünket szabad vágni, és bármennyi rendelkezésre áll belőle. A földre nem tudunk vonalakat húzni, de karót bárhol leszúrhatunk, és közéjük kötelet is kifeszíthetünk. Ezen kívül képesek vagyunk arra, hogy ha egy görbe két objektumot összekötő egyenest metsz, akkor a görbén mozogva megálljunk ott, ahol a két objektum épp azonos irányba esik tőlünk. Figyelem: ami előttünk és ami mögöttünk van, azok nem egy irányba esnek, hanem éppen ellentétes irányba!

Ezt az utóbbi lehetőséget nagyon sokan félreértették – itt ugye arról van szó, hogy megállunk, amikor két objektumot egymással éppen takarásban lévőnek látunk, vagyis ez azt feltételezi, hogy arra nézünk, amerre az objektumok vannak. Sokan úgy gondolták, hogy hátul is van szemünk, és ezért le tudunk szúrni egy karót a két fát képzeletben összekötő egyenesen, ahogy az ábrán látszódik. De az ábra csak illusztráció, a szaggatott egyenes nem áll rendelkezésre, és mivel hátul nincsen szemünk, ezért nem is tudunk ilyen könnyen karót szúrni erre az egyenesre. Természetesen kibúvó lenne, ha leszúrnánk két karót, és végtelen sok lépésben addig igazítgatnánk őket, amíg végre egy egyenesbe kerülnének a fákkal. Ezt a gyakorlatban meg lehet tenni, mert a karóknak amúgy is van egy véges vastagságuk, de ha precíz szerkesztési feladatként tekintünk, akkor nem megengedett a végtelen iteráció. Ahogy matematikaórán sem megengedett a végtelen sok lépésből álló szerkesztési eljárás, és a teljes pontosságot is megköveteli a tanár, még akkor is, ha a valóságos papíron a ceruza vastagsága miatt ez soha nem teljesül.

Sokan javasoltak különféle trükkös fizikai megoldásokat is, például azt, hogy kössünk egy karót a kötél végére, és dobjuk el az egyik fához úgy, hogy beleakadjon, vagy pörgessük a kötelet a fejünk fölött, amíg a vége bele nem ütközik az egyik fába. A feladat nem állította, hogy a fák olyan közel lennének, hogy el tudjunk odáig bármit is dobni – az ábra, ahogy már említettem, csak illusztráció volt, és nem ezen az ábrán kellett elvégezni a mérést (vagy a szerkesztést), hanem egy általános módszert kellett találni, ami minden szituációra működik. (Arról már ne is beszéljünk, hogy egy pörgő kötél egyáltalán nem egyenes.)

A feladatot természetesen többféleképpen is meg lehet oldani, de mivel a két fa sokkal nagyobb távolságra is lehet egymástól, mint ami egyáltalán kiférne a szigetre, ezért a köztük lévő távolságot valahogyan le kell kicsinyíteni, hogy a szigetre férjen, majd a lekicsinyített távolságot a megmérése után visszaszorozni. Mint látni fogjuk, ehhez nem is lesz szükség arra, hogy a két fát összekötő egyenesen pontot vegyünk fel, mert általános helyzetű segédpontokkal is dolgozhatunk. Sőt, ez a módszer akkor is működni fog, ha a fákat összekötő egyenes nem is megy át a szigeten, ahogy azt Tóth László megoldónk ábrája is mutatja.

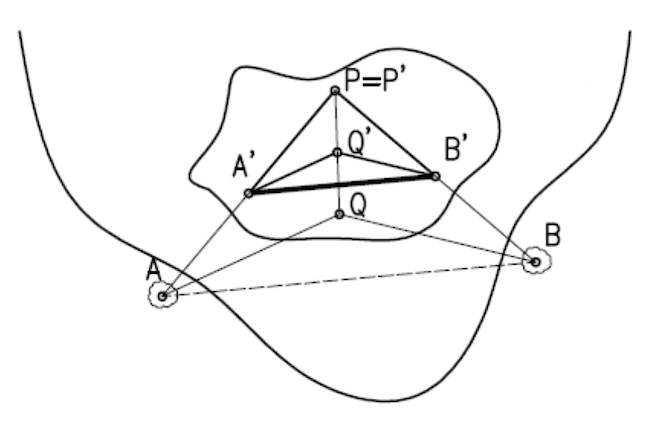
A lényeg az, hogy felveszünk egy P és egy Q segédpontot, majd az {A, B, P, Q} ponthalmazt lekicsinyítjük a P-be összehúzva úgy, hogy az {A', B', P', Q'} ponthalmaz k-ad része legyen az eredetinek. Az ábrán k = 2, azaz felére zsugorítottuk a ponthalmazt, de ha ez nem lenne elég, mert az A' vagy B' még így sem esne a szigetre, akkor nagyobb k-t kell választani. Elegendően nagy k-t választva mindenképpen a szigetre fognak esni az A', B' és Q' pontok, a P pedig helyben marad. A k-t legegyszerűbb egy elegendően nagy kettő hatványnak választani, mert kötelet felezgetni hajtogatással könnyű.

A kicsinyítés nem jelent mást, minthogy egy hasonló alakzatot kell kiszerkeszteni, például a PQA háromszöghöz hasonló PQ'A' háromszöget. Két háromszög akkor hasonló, ha a szögei azonosak, és egy háromszöget két szöge már meghatároz. Mivel a PQA háromszögnek két szöge a szigetre esik, így ha ezeket a szögeket tudnánk másolni, akkor bárhová tudnánk a PQA háromszöghöz hasonló háromszöget készíteni. Sőt, ha a P pontból kicsinyítünk, akkor elegendő csak a PQA szög átmásolása a Q'-be. Szögek másolása viszont kötelekkel és karókkal nem nehéz, hiszen egy háromszöget az oldalai meghatároznak, így kötelekből kifeszítve tudunk háromszöget másolni, ha annak minden pontja a szigetre esik, márpedig egy szög másolásához mindig tudunk elegendően kicsi háromszöget választani, amelynek egyik szöge a másolandó szög.

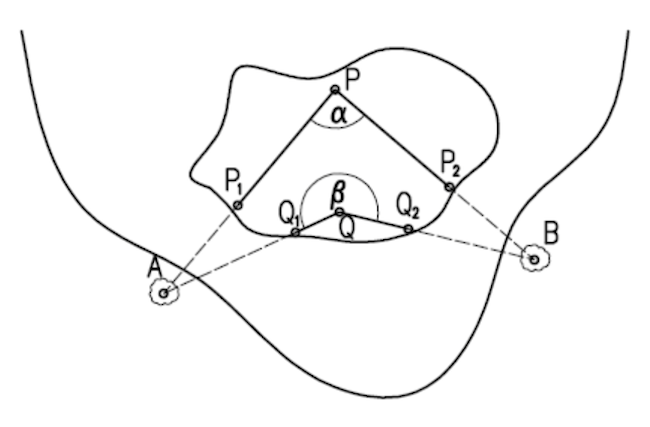
Egy probléma van már csak: a PQA szög vagy a QPA szög felvételéhez például szükségünk lenne egy Q és A közé eső Q₁ pontra, vagy egy P és A közé eső P₁ pontra, így viszont ismét azzal a problémával találjuk szembe magunkat, hogy nincsen hátul szemünk, ezért ezeket nem tudjuk felvenni. Igen ám, de a P és Q pontok helyzete nem kitüntetett, ezért nem ezeket vesszük fel előbb, hanem felveszünk egy P₁ és P₂ pontot a sziget széléhez közel, és az AP₁ és BP₂ egyenesek metszéspontját választjuk P-nek. Hasonlóképp felveszünk Q₁ és Q₂ pontokat kicsit odébb, majd az AQ₁ és BQ₂ egyenesek metszéspontját választjuk Q-nak. Ezeket már meg tudjuk szerkeszteni kötelekkel a feladat feltételei szerint.

Összefoglalva tehát: előbb felveszünk P₁, P₂, Q₁ és Q₂ pontokat, amikből megszerkesztjük a P és Q pontokat. Előbbiekere csak annyi a feltétel, hogy P és Q pontok a szigetre essenek – véges sok próbálkozással ez elérhető, ha elsőre nem sikerülne. Ezután PQ többszöri felezésével kijelöljük Q'-t, majd a PQQ₁ szöget felvesszük és átmásoljuk Q'-be, a PQQ₂ szöget pedig a másik oldalra. Így meg tudjuk szerkeszteni az A' és B' pontokat. Ha ezek nem esnének a szigetre, akkor tovább kicsinyítünk, azaz felezzük a PQ' szakaszt, és megismételjük a szögek másolását. Véges sok lépésben biztosan célba érünk, mert a sziget véges méretű. Amikor végül A' és B' a szigetre esik, akkor lemérjük a távolságukat, és megfelelő mennyiségű duplázással előállítjuk a valódi AB távolságnak megfelelő kötélhosszt.