Két héttel ezelőtt már említettük a Bizonyítások A Könyvből című könyvet, amelyben a szerzők a matematikatörténet eddigi legszebb bizonyításait igyekeztek összegyűjteni. Eredetileg Erdős Pál 85. születésnapjára szánták, aki gyakran beszélt A Könyvről, melyben Isten a matematikai tételek tökéletes bizonyításait őrzi. Sajnos Erdős 83 évesen elhunyt, de a szóban forgó könyv már sokadik kiadását éli, és a benne szereplő témák is őrzik emlékét, hiszen számos kérdésfelvetés és bizonyítás is hozzá köthető.

A könyvben szereplő egyik kedvenc részem a múzeumok őrzésének problámaköre. Az eredeti problémát Victor Klee vetette fel 1973-ban. A kérdés az, hogy hány őrre van szükség ahhoz, hogy egy n oldalú sokszög alakú kiállítótermet fix helyen álló őrök őrizzenek, azaz együtt a kiállító terem minden pontját beláthassák. Konvex sokszög esetén természetesen egy őr elegendő, de az alábbi konkáv esetben például könnyen belátható, hogy legalább harmadannyi őr kell (m), mint amennyi az oldalak száma (n = 3m). Az állítás az, hogy ennyi általában is elegendő, azaz [n/3], ahol [ ] az egészrész jele.

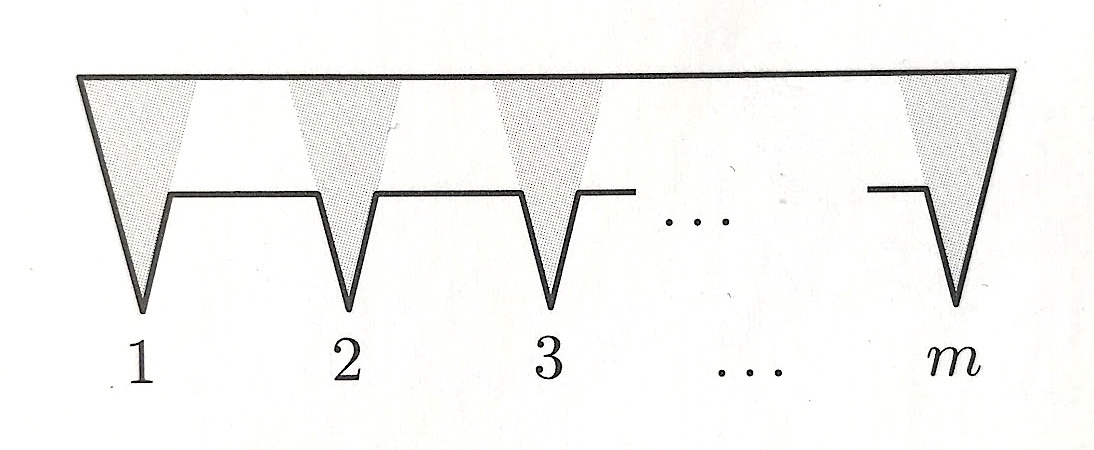
A feladatnak sok változata létezik, például feltehetjük, hogy a képek a falakon lógnak, és elegendő csak a falakat őrizni. Vagy megengedhetjük, hogy az őrök mozogjanak, például mindegyik egy adott fal mentén oda-vissza. Ez utóbbi például egy igen nehéznek látszó, egyelőre megoldatlan probléma. Egy ebbe a problémakörbe tartozó feladat az alábbi, amelyre az első helyes megoldó Válogatás Erdős Pál kedvenc feladataiból című könyvet kap ajándékba a Typotex Kiadó jóvoltából.

193. feladvány: Szabadtéri kiállítás őrzése

Tegyük fel, hogy nem múzeumot kell őrizni, hanem egy szabadtéri kiállítást, olyat például, mint egy köztéri fotókiállítás vagy az óriásplakát-kiállítás, ahol a plakáttartó állványok minkét teljes oldala kiállító felület. A kérdés az, hogy n darab állvány esetén, legrosszabb esetben hány fix pozícióban álló (pontszerű) őrre van szükség ahhoz, hogy az őrök összességében a kiállított plakátok minden pontjára, azaz az állványok minkét teljes oldalára ráláthassanak? Az állványokat úgy képzeljük el, mint egymással nem érintkező véges hosszú egyenes szakaszokat a síkon, lásd az alábbi ábrát. Tegyük fel továbbá, hogy abban az esetben, ha egy őr pont egy vonalban áll egy állvánnyal, akkor annak egyik felét sem látja. A feladat megoldása során a bevezetőben említett eredményeket fel lehet használni. Ha valakinek nem megy általánosan, akkor próbálja megoldani kisebb n-re, például n = 6 esetére a feladatot!

Nehézségi szint:

A megfejtéseket részletes magyarázattal és a szükséges ábrákkal együtt az eszventura@qubit.hu címre várjuk. A leggyorsabb és legkreatívabb megoldást küldő versenyzőink felkerülnek az Ész Ventura dicsőségfalára – közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. A versenyről minden tudnivaló megtalálható: itt. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: december 25. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.

Címlapkép: Fortepan / Hunyady József