180. feladványunkban az volt a kérdés, hogy hány különböző útvonalon haladva olvasható ki a qubit szó az alábbi ábrán, ha csak élszomszédosan haladhatunk, de akár visszafele vagy kanyarogva is olvashatunk?

A feladványban több trükk is volt, amit kevesen vettek észre. Ez nem csak egy leszámolásos feladat volt, hanem észlelési feladat is. Azt könnyen észlelte mindenki, hogy az ábra közepén nincs t betű, de azt már nagyon kevesen, hogy az egyik helyen, lásd a piros foltot az alábbi ábrán, egy q betű megtöri a szimmetrikus mintázatot.

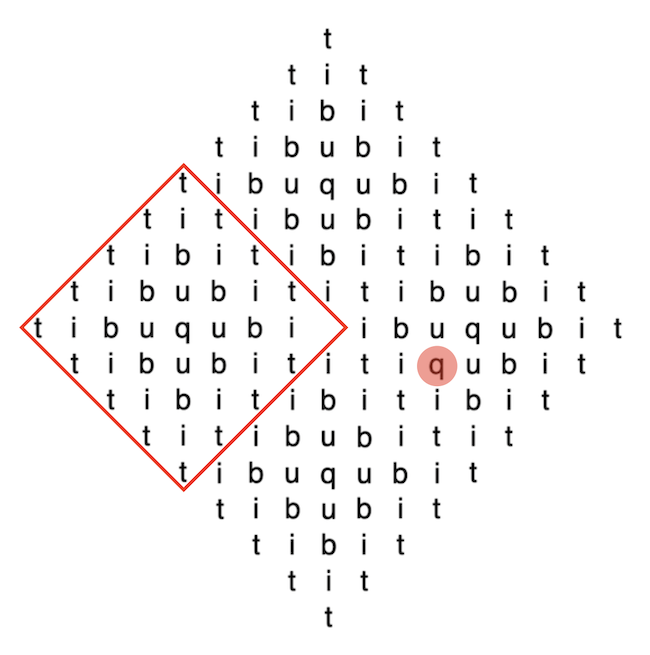
Ezen kívül a leszámoláshoz érdemes valamilyen matematikai trükköt alkalmazni, mert egyesével hosszadalmas lenne. Tekintsük először az egyik negyedet, amit az ábrán pirossal bekereteztünk. Számoljuk le, hogy ezen a kereten belül hány különböző útvonalon haladva lenne kiolvasható ki a qubit szó, ha a hiányzó t betű is ott lenne. A szót nyilvánvalóan az egyetlen q betűből indíthatjuk, és nem is juthatunk a kereten kívülre. A q-ból négyfelé indulhatunk valamelyik u betű felé. Nézzük meg, hogy hány útvonal van, ami átmegy egy adott u betűn.

Nézzük a fenti ábrán látható esetet, amikor jobbra indulunk. Az u betű után mindig vagy csak jobbra és felfele, vagy csak jobbra és lefele haladhatunk, de ezt figyelembe véve minden útvonal lehetséges. Ha a jobbra és felfele irányokból választunk minden lépésben az u betűtől kezdve, akkor ez 2·2·2 = 8 különböző lehetséges útvonal, amely fekete és piros nyilakból áll. Ha a jobbra és lefele irányokból választunk, akkor szintén 8 útvonal lehetséges, amelyek fekete és kék nyilakból állnak, viszont a két halmaz között van egyetlen közös útvonal, amikor végig csak jobbra haladunk a fekete nyilak mentén. Ha tehát a q-ból jobbra indulunk, akkor 8 + 8 - 1 = 15 különböző útvonal lehetséges.

Ugyanennyi útvonal lehetséges a többi irányba is, ezért egy q-ból összesen 4·15 = 60 darab út menne, ha minden t betű a helyén lenne. A hiányzó t betű viszont csak egyetlen útvonalat gátol, tehát 59 útvonal tartozna az ábra minden negyedéhez, ha a piros folt helyén nem törne meg a mintázat, ami összesen 236 qubit.

De mit okoz a rácshiba? A b betű helyén lévő q betű a fenti leszámolásban elront néhány útvonalat, de egyúttal keletkeznek is új qubit szavak. Könnyen belátható, hogy 2·4 = 8 qubit romlik el, mert kétféleképpen juthatunk az elrontott betűig, és onnan 4 féle módon folytathatjuk. A plusz q betűből viszont 21 új qubit indul ki. Ezt legkönnyebben úgy tudjuk összeszámolni, ha megnézzük, hogy melyik b betűkhöz juthatunk el, és megnézzük, hogy az egyes b betűkből hányféleképpen fejezhetjük be. Vigyázat: egyes b betűkből 4 féle befejezés lenne lehetséges, másokból 7, de az ábra közepén kimaradó t betű miatt az egyik útvonal nem tud megvalósulni.

Ha mindent összeszámolunk, akkor a helyes válasz 236 - 8 + 21 = 249.