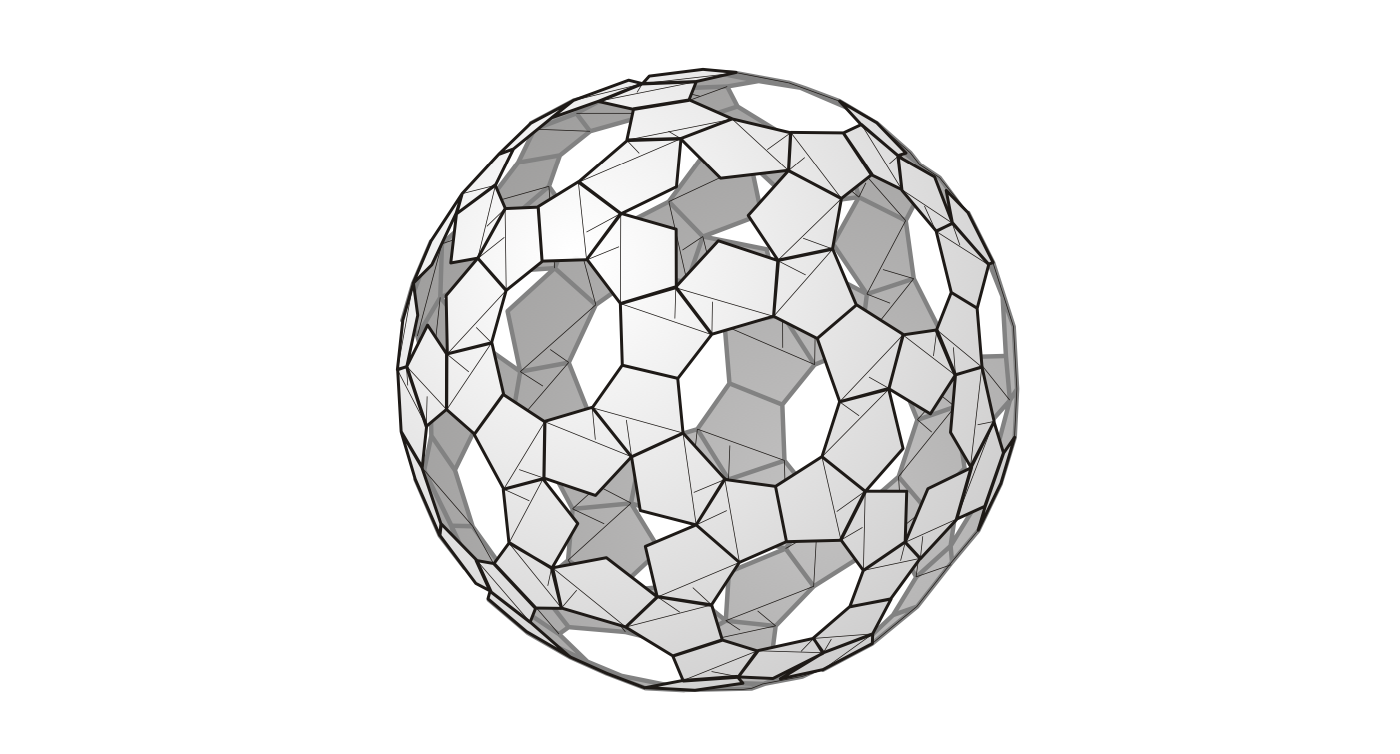
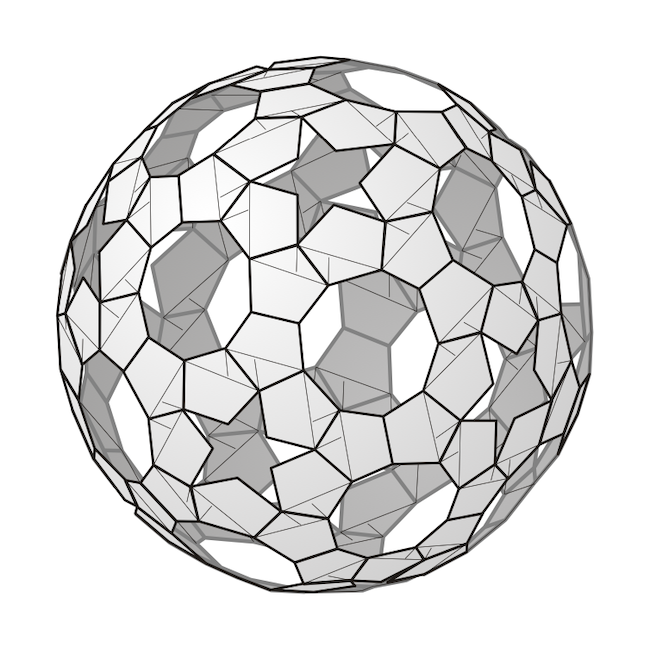
189. feladványunkban az volt a kérdés, hogy milyen hosszú papírcsíkra van szükségünk ahhoz, hogy elkészítsük Heinz Strobl Sphere94 nevű gömbjét hajtogatott, azaz lelapított papírcsomókból.

A knotology névre keresztelt hajtogatási módszer szerint szabályos ötszögekből építkezhetünk, amiket egy papírcsíkból kötött és lelapított csomó alkot, ahogy az alábbi ábra is mutatja.

Ha egy ilyen csomót kihajtunk, akkor azt láthatjuk, hogy valójában négy trapézra volt szükségünk az elkészítéséhez.

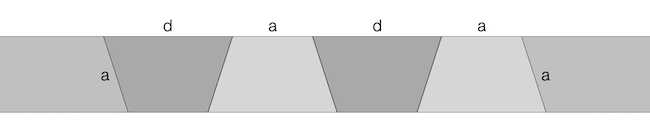
Első lépésként meg kell határozni a 2 cm széles szalagból meghajtott szabályos ötszög oldalát (a), majd átlójának a hosszát (d). Az ötszög egy oldalának és a vele párhuzamos átlójának távolsága lesz a 2 cm. A kedves olvasóra bízom az elemi geometriai számítást, ami alapján az ötszög oldalára a ≈ 2,103 cm, az átlójára pedig d ≈ 3,403 cm adódik. Egy ötszög elkészítéséhez négy trapézból álló paralelogrammára van szükségünk, amelynek hosszanti középvonala 2a + 2d hosszúságú, azaz 11,012 cm. A teljes gömbben 120 ötszög látható, ezért 1321,44 centiméternyi szalag biztosan kell.

Természetesen az ötszögeket jó lenne összefűzni, és nem összeragasztani őket. Ha nem is egy csíkból készítjük el az egészet, de a gyakorlatban érdemes modulokat használni. A linkelt dokumentumban például az alábbi csillag alakzatot javasolja a szerző modulnak, amelyből tizenkettőre van szükség a teljes gömb elkészítéséhez. Ezt a csillag alakzatot azonban nem tudjuk közvetlenül a fenti szimpla ötszögek használatával összefűzni, mert az is számít, hogy a csomóból hol távozik a papírcsík két vége, és milyen szögben. Ez a fenti szimpla csomó esetében nem lenne megfelelő.

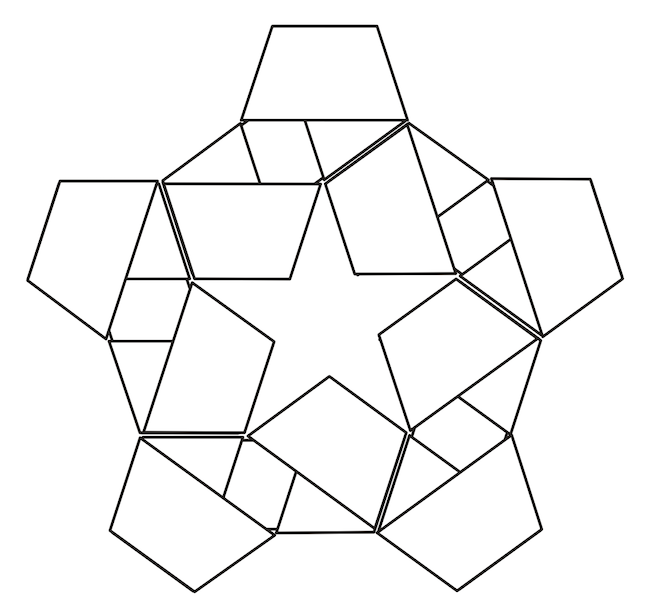
Ahhoz hogy a fenti csillag alakzatot egy folytonos papírcsíkból meg tudjuk fűzni, az alábbi, úgynevezett dupla és tripla csomókra lesz szükségünk, amelyeknél a papírcsíkot még egyszer vagy kétszer visszafűzzük (részletesebben lásd a korábban linkelt dokumentumban). A visszafűzés mindig két újabb trapézt használ fel, ezért ezekhez a csomókhoz rendre 3a + 3d ≈ 16,518 cm és 4a + 4d ≈ 22,024 cm hosszúságú csíkokra lesz szükségünk, ha a középvonalakat tekintjük.

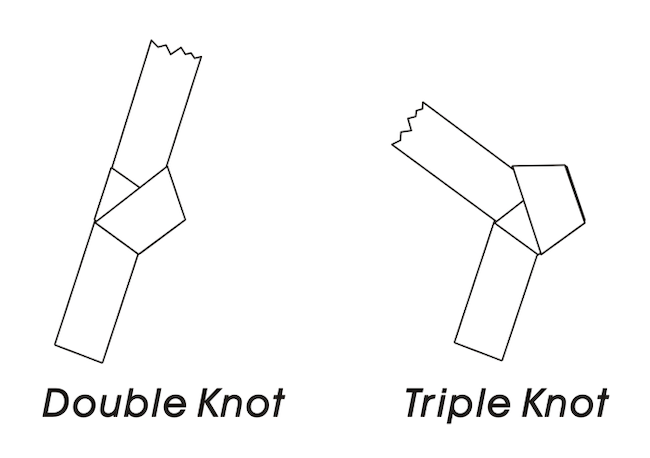
Mindkét csomóból öt darab kell, tehát a teljes csillag alakzatra összesen 35a + 35b ≈ 192,71 cm hosszú csíkot kell szánnunk, amiből 12 kell a teljes gömbhöz, ami 2312,52 cm-t, azaz több mint 23 métert ad ki. És akkor még nem számoltuk bele azt, hogy még össze is kell kötnünk a csillag alakzatokat.

Természetesen kérdés, hogy abban az esetben, ha tényleg egyetlen papírcsíkból szeretnénk elkészíteni a gömböt, akkor ezt pontosan milyen vonalvezetés mentén érdemes tenni ahhoz, hogy a lehető legrövidebb szalagot használjuk. Az is lehet, hogy nem is csillag alakzatokból érdemes építkezni. Különdíjért továbbra is várjuk az optimális megoldást az eszventura@qubit.hu címre! Beküldési határidő: április 30. éjfél.

A különdíj: Martin Gardner Szórakoztató matematikai fejtörők című könyve a Typotex Kiadó jóvoltából és egy Csodák Palotája családi belépő.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.