192. feladványunkban az volt a kérdés, hogy legkevesebb hány metszéspontja lehet egy konvex hatszög átlóinak. Sejthető, hogy a választ a szabályos hatszög fogja szolgáltatni, hiszen az a legszimmetrikusabb, tehát ha bizonyos metszéspontok egybe tudnak esni, akkor a szabályos hatszögnél ez várhatóan megtörténik.

Az alábbi ábrán láthatjuk, hogy szabályos hatszög esetén a metszéspontok száma 13, és egybeeső metszéspont csak középen van, a szemközti csúcsokat összekötő átlók közös metszéspontjában. A feladat tehát csak annyi lenne, hogy belássuk, ennél kevesebb metszéspont nem lehet.

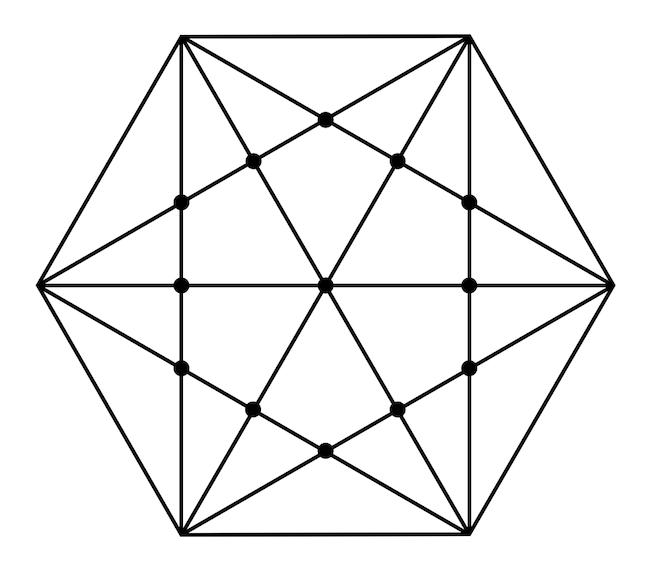
De hogyan lehet bizonyítani?

Könnyen belátható deformált hatszög esetében is a konvexitás miatt, ha veszünk egy tetszőleges csúcsot (lásd az 1-es csúcsot az ábrán), akkor a két szomszédját összekötő átlót (kék) a csúcsból kiinduló három átló (narancsok) három különböző pontban metszi, és a szemközti csúcsba futó átlóhoz tartozó metszéspont lesz középen, vagyis a másik két metszéspont közé fog esni.

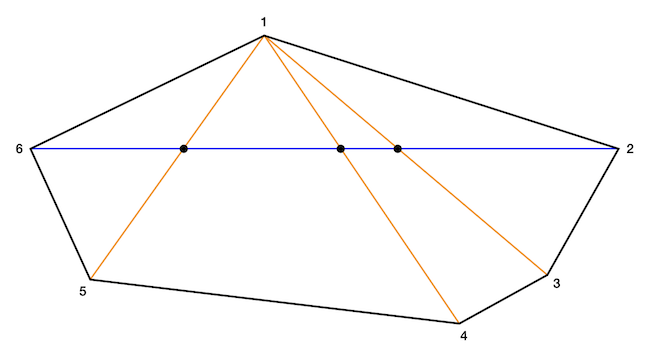
Ezek után, ha vesszük az 2-4-6 csúcsok alkotta háromszöget, akkor biztos, hogy a háromszög minden oldalára fog esni három különböző metszéspont, ezek ugyanis egymást nem metsző hatszög átlók. Ezek között a metszéspontok között lesz például az 1-3 és 2-6 átlók metszéspontja, továbbá az 1-3 és 2-4 átlók metszéspontja. E két metszésponton át fektetett egyenes éppen az 1-3 átló, amin viszont ott kell lennie a két előbbi metszéspont között egy tőlük különböző metszéspontnak is: az 1-3 és 2-5 átlók metszéspontjának. Ugyanígy a 3-5 és 5-1 átlók esetében is találunk még egy-egy plusz metszéspontot a már számba vett metszéspontok között.

Ezzel tehát megkaptuk a másodszomszédos átlók 12 metszéspontját, amikről beláttuk, hogy mind különbözőek, már csak azt kéne belátni, hogy ezek egyikével sem eshet egybe az egyik szemközti csúcsokat összekötő átlók metszéspontja, hiszen akkor legalább még egy metszéspont kell. Ez viszont nyilvánvaló, hiszen mondjuk a 2-6 másodszomszédos átlón lévő metszéspontok (lásd a fekete pöttyöket az ábrán) egyike sincs rajta sem a 2-5, sem a 3-6 szemközti pontokat összekötő átlón, tehát nem lehetnek szemközti pontokat összekötő átlók metszéspontjai, mert összesen csak három ilyen, szemközti pontokat összekötő átlója van a hatszögnek.

Egyébként érdekesség, hogy általában véve ez egy igen nehéz kérdésnek tűnik. Hatszögre könnyen elbántunk a feladattal, de ha megnézzük a sorozatok online enciklopédiáját (OEIS), akkor azt láthatjuk, hogy kilencszögre egyelőre még nem ismert a pontos válasz.