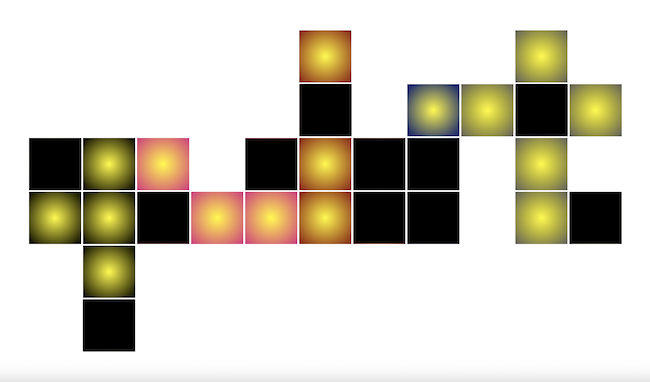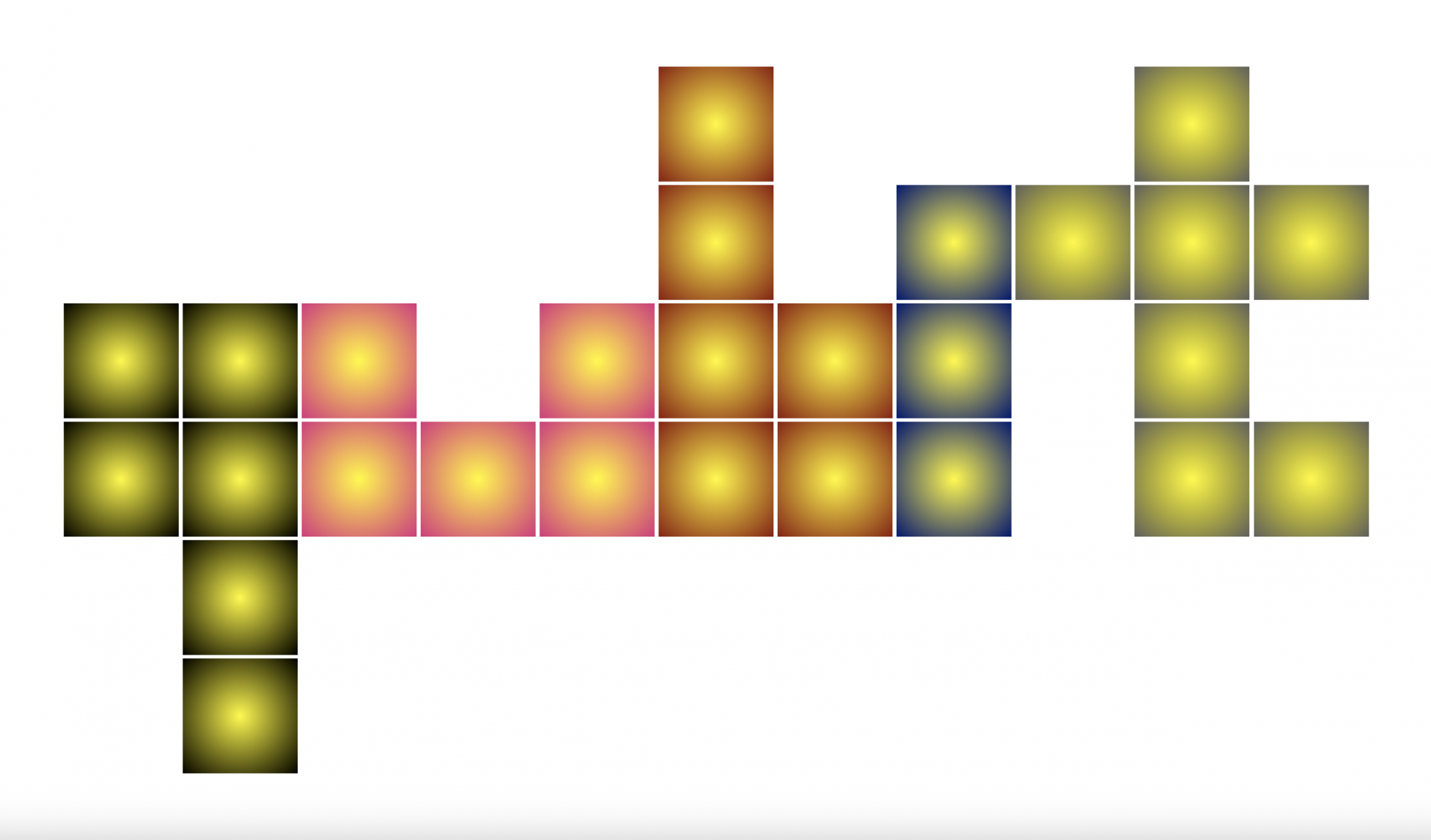195. feladványunkban az volt a kérdés, hogy hogyan tudunk minden lámpát lekapcsolni, ha a villanykapcsolók úgy működnek minden szobában, hogy amikor megnyomjuk, akkor nemcsak abban a szobában, hanem az összes oldalfal mentén szomszédos szobában is átvált a lámpa, vagyis égő állapotból lekapcsolt állapotúra, lekapcsolt állapotból pedig égő állapotúra változik.

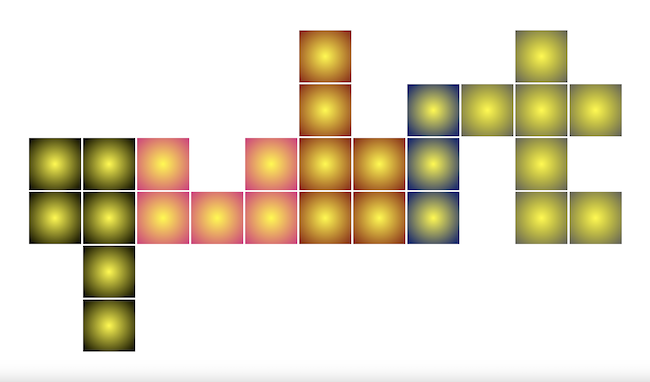
Első észrevételünk az lehet, hogy egy villanykapcsolót nem érdemes egynél többször átkapcsolni, mert két kapcsolással ugyanazt érjük el, mintha egyszer sem nyúltunk volna hozzá. Így legalább tizenegy kapcsolás szükséges, ahogy az alábbi ábrán is látszik, ahol a fekete négyzetek jelölik azokat a szobákat, amelyekben meg kell nyomni a kapcsolót. Könnyen ellenőrizhető, hogy minden szobára teljesül külön-külön (a feketéket is beleértve), hogy az élszomszédait és önmagát is belevéve páratlan sok fekete van közöttük, ez kell ugyanis ahhoz, hogy a végén sötét legyen mindenhol.

Egyébként bárhogy rajzolnánk a szobákat, mindig lenne megoldás, vagyis abban az esetben, ha az elején mindenhol fel van kapcsolva a villany, mindig elérhető, hogy lekapcsoljuk mindenhol. Ezt Mérő László már bebizonyította 40 évvel ezelőtt egy KöMaL cikkben, de próbáljátok meg ti is!