Takarékos karácsony

224. feladvány: Karácsonyi darabolás
Végtelen sok barátunknak végtelen sok ajándékát már becsomagoltuk dobozokba, de szeretnénk mindegyik csomagra egy kis karácsonyi dekorációt is tenni. A dekorációhoz A4-es papírlapból az alábbi, fenyőfát imitáló háromszöget vágunk ki. A fenyőfa csúcsa az A4-es lap rövidebbik oldalának épp a felezőpontjára esik. Ezt a zöld háromszöget szeretnénk végtelen sok, ehhez (geometriai értelemben) hasonló háromszögre felvágni, hogy az egyes háromszögeket a csomagokra ragaszthassuk dekoráció gyanánt. Az alábbi feltételeket be kell tartani:
- csak egy réteg papírt vághatunk, tehát nem hajtogathatunk,
- csak egyenes vágásokat tehetünk,
- minden vágás után fel kell ragasztanunk egy dekorációt egy csomagra,
- minden barátunknak más méretű dekorációt szeretnénk
- és nem szeretnénk pazarolni, azaz a zöld részből nem maradhat maradék.
Fel lehet darabolni a fenti feltételeknek megfelelően az egyenlő szárú zöld háromszöget?

Tipp
Gondolkodhatunk az eredetitől eltérő állású háromszögekben is, például olyanokban, amik a szárukon fekszenek. Továbbá ne felejtsük el, hogy a háromszög szögeinek összege 180 fok, ami pont egyenesszög.
Megoldás
Egy lehetséges ötlet a következő darabolás.
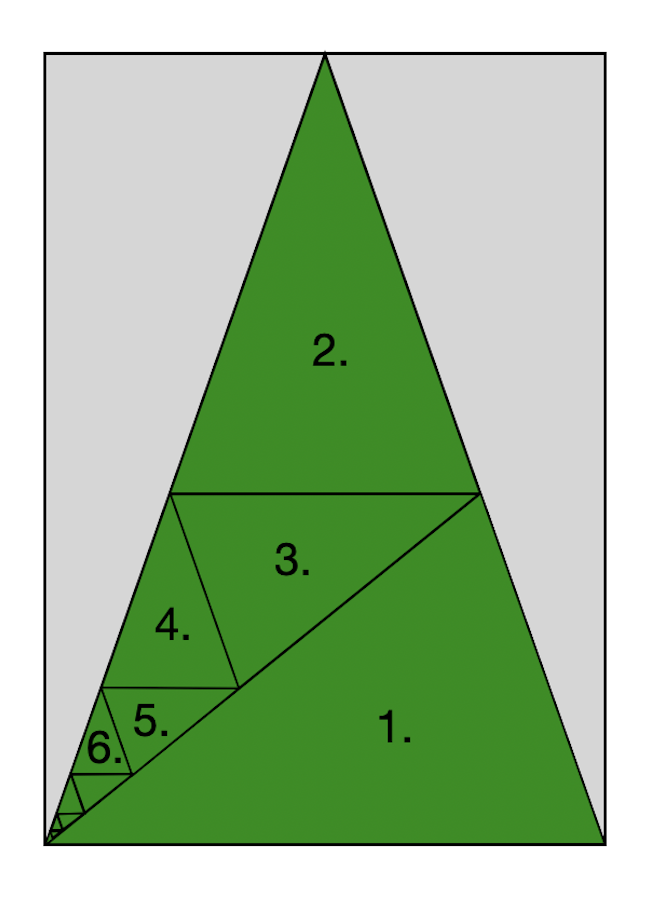
Mielőtt azonban ezt elfogadjuk, három dolgot ellenőrizni kell: hogy tényleg hasonlóak-e a háromszögek, hogy vágásonként egy háromszög leesik-e, illetve hogy különböző méretűek-e.
Az 1-es sorszámmal jelölt háromszöget levághatjuk úgy, hogy egyenlő szárú legyen, és egyik szöge (jobb alsó) az eredetivel megegyezik, így a háromszög is hasonló lesz az eredetihez. Hasonlóan a 2-es sorszámú háromszögnek is van az eredetivel megegyező szöge (a szárszöge), és ha az alapok párhuzamosak egymással, akkor ezek is hasonlóak lesznek. A 3-as sorszámú háromszögnek pedig azért lesz a szárszöge (a két szár közötti szöge) megfelelő, mert az 1-es, 2-es és 3-as háromszög közös csúcsában találkozó szögek épp egy egyenesszöget adnak ki, ami egyben a háromszög szögeinek összege. Innentől kezdve teljesen hasonló módon adódik, hogy a 4-es szárszöge is épp megfelelő, mert a 2-es, 3-as és 4-es háromszög közös csúcsában találkozó szögek összege is 180 fok, és így tovább. A hasonlóság tehát belátható, ha pedig az ábrán jelölt sorszámok szerinti sorrendben haladunk, akkor az is látható, hogy minden egyes vágással keletkezik egy új háromszög, amit a későbbiekben már nem kell tovább vágunk, tehát fel tudjuk azonnal ragasztani.
Amit még ellenőriznünk kell, hogy a háromszögek méretei különböznek. A 3-as sorszámútól kezdve ez nyilvánvaló, mert minden levágott háromszög szára az előző levágott háromszögnek az alapja, tehát ugyanazzal a kicsinyítési faktorral kapjuk a következő levágott háromszög méretét. A kérdés csak az, hogy az 1-es és 2-es sorszámú háromszögek méretei is különböznek-e. Ez látszólag így van, ha kipróbáljuk egy A4-es lappal, ahogy az a méretarányos illusztráción is látszik, de azért érdemes kiszámolni ellenőrzés végett. Ezt a részt meghagyom a kedves olvasónak.
Bónusz kérdések karácsonyi meglepetésajándékért az első megfejtőknek: A fenti darabolás szerint mennyi papír marad, ha 100 barátunk van? Hány dekorációt tudunk készíteni, ha 1 cm-nél alacsonyabb háromszöget már nem szeretnénk használni? Tudtok-e más darabolási módszert, ami megfelel a fenti feltételeknek? A megoldásokat az eszventura@qubit.hu címre lehet küldeni karácsonyig!
Ha szereted a fejtörőket, tekintsd meg korábbi feladványainkat is. Ha megjegyzésed lenne, vagy feladványt javasolnál, írj az eszventura@qubit.hu e-mail címre. Ha pedig tetszik a rovat, akkor ezt a Vendégkönyvben kifejezésre juttathatod.
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.
