A játék várható nyereményét kellene kiszámítani. Érdemes az eseteket aszerint szétválasztani, hogy hányadik körben dobod az első END-et. A korábbi dobásoknál körönként fix átlagnyereménnyel lehet számolni.

Az END valószínűsége egy dobásnál 1/6, a nyeremény növelésének a valószínűsége pedig 5/6, és a nyeremény átlagosan három dollárral nő, ha nincs vége a játéknak. A teljes nyeremény várható értékét úgy kapjuk, hogy az egyes esetekben elérhető teljes nyereményeket az esetek valószínűségeivel súlyozzuk, és ezeket összeadjuk. Jelen esetben az eseteket aszerint érdemes szétválasztani, hogy hányadik körben dobjuk az első END-et, azaz hány dobásból áll a játék.

Annak a valószínűsége, hogy a játék az első körben véget ér, éppen 1/6, és ekkor 0 dollár a nyereményünk. Annak a valószínűsége, hogy pontosan a második körben ér véget a játék (5/6)·(1/6), ebben az esetben pedig a nyeremény átlagosan 3 dollár. Annak a valószínűsége, hogy pontosan a harmadik körben ér véget a játék (5/6)·(5/6)·(1/6), ebben az esetben pedig a nyeremény átlagosan 2·3 dollár, azaz 6 dollár. És így tovább, annak a valószínűsége, hogy a k. körben, azaz k. dobásra ér véget a játék, ahhoz az kell, hogy (k-1) körön keresztül ne dobjunk END-et, a k. körben viszont END-et dobjunk.

Összesítve tehát a teljes nyeremény várható értéke ebben a játékban az alábbi végtelen összeggel adható meg:

(1/6)·0 + (5/6)·(1/6)·3 + (5/6)·(5/6)·(1/6)·6 + (5/6)·(5/6)·(5/6)·(1/6)·9 + ...

Mivel minden tagban szerepel az (1/6) és a 3-as is kiemelhető, ezért egyszerűsítve így írhatjuk:

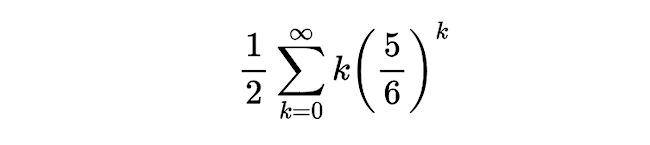
Itt a lényeges rész a végtelen összeg, amiben a tagok egy mértani és egy számtani sorozatnak a tagjai összeszorozva. Ezt nevezik számtani-mértani sornak, amire létezik zárt összegképlet. Nevezzük el az 1/2 mellett lévő végtelen szummát S-nek. Ha képezzük az S - (5/6)·S sort úgy, hogy (5/6)·S-ben tagonként szorzunk (5/6)-dal, majd a kivonásnál az (5/6) azonos hatványait vonjuk ki egymásból, azaz a sorokat eggyel elcsúsztatjuk, akkor a maradék egy mértani sorozat lesz, aminek a végtelen sorösszegét jól ismerjük. Ha végigszámoljuk, akkor S-re 30 adódik, vagyis 15 dollár ennek a játéknak a várható nyereménye.

Ez azt jelenti, hogyha jól szeretnénk járni várható értékben, akkor 15 dollárnál ne fizessünk többet egy ilyen játékért. Ugyanakkor meg kell jegyezni, hogy az eloszlás nem egyenletes, tehát kis valószínűséggel lehet nagy nyereményünk, elvileg akármilyen nagy, és aki kockázatvállaló, és sok pénzre van szüksége, annak egyéni preferenciái szerint megérheti nagyobb összegért is játszani.