Az előző heti Bongard-problémát elsőre nagyon sokan félreértették, annak ellenére, hogy elég részletes volt hozzá a leírás. Úgy látszik, hogy mégsem volt elég személetes, pedig az agyunk állandóan hasonló problémákat old meg ösztönösen, hiszen folyamatosan összefüggéseket és mintázatokat keresünk, továbbá kategóriákat állítunk fel. Néha ott is látunk mintázatot, ahol nincs, de az agyunk képtelen tőle elszakadni. Ezen alapul sok optikai illúzió, vagy gondoljunk például az arcra a Marson.

Nagyon sok olyan probléma van egyébként, amikben ösztönösen nagyon jól teljesítünk, de nem tudjuk tudatosítani, vagy ha tudatosítjuk, akkor romlik a teljesítmény, mert az agyunk tudatosabb része belekontárkodik az egyébként automatikusan működő megoldási sémába. Jelen esetben is biztos vagyok benne, ha nem az lett volna a kérdés, hogy magyarázzuk meg a különbséget, hanem egy 13. ábrát kellett volna balra vagy jobbra besorolni, akkor az ösztöne valószínűleg mindenkinek jól súgta volna meg a megoldást.

Ez is csak egy (bocsánat hat) kakukktojás

Visszatérve a feladat mibenlétére, a Bongard-probléma lényegében nem más, mint a klasszikus kakukktojás-feladat általánosítása, csak itt 12 ábra van és 6 kakukktojás. Ha valakinek nem lett volna egyértelmű, vagy még mindig nem világos, akkor érdemes néhány egyszerűbb Bongard-problémával kezdeni, és akkor az ember hamar ráérez. A neten sok Bongard-problémát lehet találni, itt van egy átfogó gyűjtemény, ahol az első 100 a Bongard könyvében megjelent eredeti problémákat tartalmazza, az utolsó 17 helyen pedig az Ész Ventura szerzőjének problémái szerepelnek, melyek mindegyike karaktereket használ ábraként, mint az itt kitűzött feladvány is.

A klasszikus kakukktojás-feladatnál egyébként általában négyből egy a kakukktojás, de a négy az viszonylag kevés, ezért ha valaki nagyon akar, akkor bármelyikre találhat magyarázatot. Egy Bongard-probléma esetében nehezebb az eredeti megoldástól gyökeresen eltérő magyarázatot találni, legfeljebb különböző megfogalmazásokat. Ezért is használják például mesterségesintelligencia-kutatásban és teszteléshez. Ugyanakkor a több ábra több támpontot is adhat a megoldáshoz. Jelen esetben például sokaknak adott támpontot, hogy a 10 az egyik, a 01 pedig a másik csoportba került, ami sok gondolkodási irányt rögtön kizárt.

Rátérve a kitűzött Bongard-problémára, sok olyan megoldást kaptam, amiben a négyzet alakú keretre vagy a vízszintes és függőleges irányokra volt hivatkozás. Fontos kihangsúlyozni, hogy a Bongard-problémák eredetileg ábrák geometriai tulajdonságaira vonatkoznak, tehát a keretet nem lenne szabad az ábrához tartozónak tekinteni, homokba is lehetne rajzolni, ahol értelmetlen még a vízszintes és függőleges irányokról való beszéd is. Ideális esetben tehát az ábrák egymáshoz viszonyított helyzete sem lényeges, elforgatva is lehetne rajzolni őket. Az ábráknak önmagukban értelmezhető és ábránként egyértelműen megítélhető geometriai tulajdonságai jöhetnek szóba.

Geometriai tulajdonság alatt pedig szemléletesen azt lehet érteni, hogy egy marslakó is megértené a különbséget, nem kell hozzá semmilyen társadalmi és kultúrális ismeret, mint amilyen például az ábécé, de ezt külön is hangsúlyoztuk a feladat szövegében.

Megoldás természetesen elképzelhető több is, és elfogadtam a fenti feltételeknek szigorúan nem megfelelő megoldásokat is, de amire eredetileg gondoltam, az az alábbi.

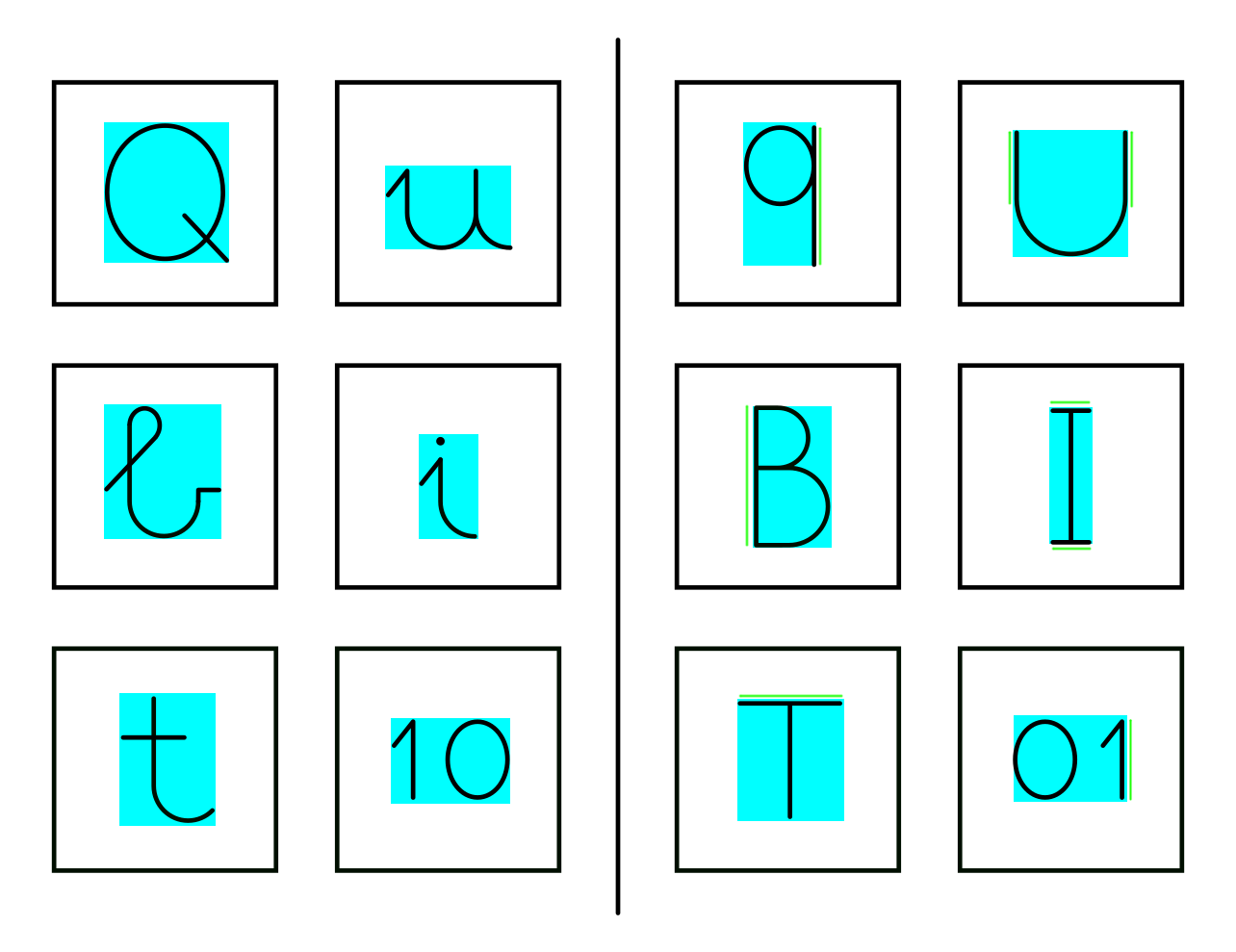
Rajzoljuk meg minden kis ábrához, azaz karakter(ek)hez, a legkisebb területű téglalapot, ami az ábrát magába foglalja. A téglalap elvileg lehetne ferde is, de a feladványban szereplő ábrák esetében a téglalapok oldalai többnyire párhuzamosak a kerettel. Van kivétel is, például a kis i betű, de ott lényegtelen lesz, hogy hogyan áll a minimális terűletű téglalap. A bal oldali ábrák ezekkel a minimális körülírt téglalapokkal mindig csak véges sok ponton érintkeznek a kerületük mentén, míg a jobb oldalon minden esetben lesz közös szakasz is, azaz végtelen sok közös pont. Ugyanezt meg lehet többféleképpen is fogalmazni, de ez a fajta megfogalmazás azért szép, mert nem használja sem a keretet, amit sokan, sem pedig a vízszintes és függőleges fogalmakat.