Miért hűl ki az asztalon hagyott étel? Ez is az entrópia növekedés törvényére vezethető vissza! Ha két különböző hőmérsékletű test érintkezik, akkor a melegebb felmelegíti a hidegebbet, miközben maga lehűl. De mi az, hogy melegebb, és mi az, hogy hidegebb? Ez a kérdés már a hőmérséklet fogalmához vezet.

Amíg a hőmennyiség a molekulák rendezetlen mozgásának együttes kinetikus energiája, addig a hőmérsékletet az egyes molekulák átlagos energiája jellemzi. Ebből indul ki a termodinamika tudománya, amikor bevezeti a hőmérséklet fogalmát. Ha minden mozgás leáll – eltekintve a kvantummechanikai bizonytalansági elvből fakadó rezgésektől – akkor beszélünk a nulla pontról az abszolút hőmérsékleti skálán, amit Kelvin skálának nevezünk. Ha a molekulák átlagos mozgási energiája megnövekszik, akkor az abszolút hőmérséklet is nagyobb lesz. A hőmennyiség és a hőmérséklet kapcsolata, pontosabban ezek aránya vezet el az entrópia klasszikus fogalmához.

Entrópia: a megfordíthatatlanság mértéke

Legyen T1 és T2 a két hőmérséklet, ahol az előbbi rendelkezik nagyobb értékkel, és a testek adjanak át egymásnak ΔQ hőt. Ekkor az első test lead ΔQ hőmennyiséget, míg a második az energiamegmaradás törvénye szerint ugyanannyit vesz fel. A hőmennyiség teljes összege tehát nem változik, de van valami, ami változni, mégpedig növekedni fog, és ez az entrópia. Matematikailag ezt úgy adjuk meg, mint az átadott hőmennyiség és a hőmérséklet hányadosát:

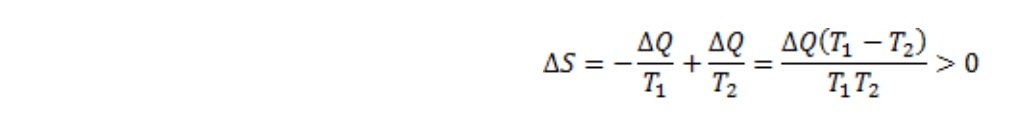
Az entrópiaváltozás mindig pozitív, ami egyenértékű avval a kijelentéssel, hogy a hő a magasabb hőmérsékletű helyről vándorol az alacsonyabb hőmérsékletű hely felé. A hőáramlás iránya – hacsak nem használunk fel valamilyen külső energiaforrást, mint például elektromos energiát a hűtőgépekben – nem fordítható meg.

Az entrópiát ezért a megfordíthatatlanság, más szóval az irreverzibilitás mértékének is tekinthetjük. Az entrópianövekedés valamennyi energiakonverzió esetén bekövetkezik: ha a test kinetikus energiáját konvertáljuk a potenciális energia valamilyen formájába, majd a folyamatot megfordítva visszanyerjük a mozgási energiát, akkor a kinetikus energia egy része mindig elvész, pontosabban hőenergiává alakul át. Ugyanez történik, amikor potenciális energiából nyerünk kinetikus energiát, majd ennek munkájával újra potenciális energiát hozunk léte: a teljes ciklus mindig hőtermeléssel jár, ennek mértékét a képzett hőmennyiség és a hőmérséklet arányával, azaz az entrópia növekedésével jellemezhetjük.

Ezt a felismerést fogalmazza meg a termodinamika második főtétele: perpetuum mobile nem építhető fel, ami egyenértékű avval a megállapítással, hogy zárt rendszerben az entrópia mindig növekszik.

Most pedig hajtsunk végre egy varázslatot!

Eddig tehát két fizikai fogalommal foglalkoztunk: az energiával és az entrópiával, az előbbi mennyiség, amelyik minden mozgásban és átalakulásban megmarad, a másik, amelyik mindig növekszik. Az előbbi képviseli a változásban az állandóságot, a második adja meg a változások irányát. Várható, hogy ez az utóbbi játszik döntő szerepet az evolúcióban is.

Mielőtt az evolúció fogalmára térnénk át, vizsgáljuk meg az entrópia fogalmának egy mélyebb értelmezését. Amit eddig elmondtunk az nem függ a vizsgált anyagok jellegétől, összetételétől, nem fontos, hogy homogén vagy inhomogén rendszerről van-e szó, csak azt kötöttük ki, hogy a rendszer zárt legyen, azaz energiacsere ne következzen be a környezettel. De felvethetjük a kérdést, hogy milyen mikroszkopikus folyamatok állnak az entrópianövekedés mögött?

Evvel a kérdéssel foglalkozik a statisztikus mechanika. Bármilyen makroszkopikus rendszerben óriási számú molekula, vagy atom van. Például a víz 18 grammjában N = 600 000 000 000 000 000 000 000 = 6x10²³ a molekulák száma. Ezt nevezzük az Avogadro-számnak. Hogy milyen óriási számról van szó, azt egy hasonlattal érzékeltetjük. Töltsünk meg egy gyűszűt vízzel, majd öntsük ki! Közben hajtsunk végre egy varázslatot: nőjön meg minden vízmolekula akkorára, mint egy pingponglabda! Ekkor a víz kifolyik a szobából, elönti először környezetünket, végigfut az országon, sőt egész Európán is, de itt sem áll meg, hanem átfut az óceánokon, és elönti az egész Földet. De olyan magasan, hogy csak a legmagasabb hegyek látszanának ki, mert a víz szintje 4 kilométer magasan lenne.

Ilyen hatalmas számú molekula mozgását egyenként lehetetlenség leírni, hiszen ehhez az összes molekula mozgását ismerni kellene. Vannak azonban olyan átlagos jellemzői a rendszernek, amellyel az egész rendszer rendelkezik. A statisztikus mechanika termodinamikai törvényei legkönnyebben az ideális gázok esetére adhatók meg. Ideálisnak tekintünk egy gázt, ha a molekulák ütközése nem hoz létre változást a molekulák szerkezetében csupán mozgásuk irányát, sebességét és kinetikus energiáját változtatja meg. A vízgőz molekuláinak ütközésekor az impulzusváltozások átlaga (impulzus = tömeg szorozva a sebességgel) kapcsolódik a nyomáshoz, a kinetikus energia átlaga a hőmérséklethez, ez a két mennyiség pedig zárt rendszerekben a gáz állapotát egyértelműen jellemzi.

Entrópia: iránytű a legvalószínűbb állapotok felé

A statisztikus mechanikában az entrópia definíciójához a valószínűség fogalmán keresztül jutunk el. Ugyanakkora hőmérséklet, amit az átlagos energiával jellemezhetünk, a részecskék energiájának sokféle eloszlásával valósulhat meg. Lehet akár mindegyik molekulának azonos energiája, sőt a mozgások iránya is megegyezhet. Valójában ez az eset valósul meg a mozgásban lévő szilárd testek esetén, mert ekkor a molekulák közötti összetartó erő egyben tartja a testet.

De képzeljük el, hogy valamilyen okból a test széthasad molekuláira! Ekkor a molekulák egymástól független mozgásokat végeznek, ami ütközésekkel jár, és a végeredmény valamilyen kaotikus mozgás lesz. Ezt a rendszert már gáznak nevezzük, ahol a molekulák a legkülönbözőbb energiával rendelkeznek. A kérdés az, hogy milyen az energiaeloszlás? Van olyan eloszlás, ami csak egyféleképp valósulhat meg, ez volt a kiinduló példa az együtt haladó molekulák esetében, de lehet olyan eset is, amikor egyetlen molekula veszi át a gáz teljes energiáját. Ilyen esetből már jóval több van, mert bármelyik molekula szóba jöhet. Természetesen ez az eloszlás is rendkívül valószínűtlen. Viszont sokkal többféle módon valósulhatnak meg az olyan eloszlások, ahol a részecskék energiája különböző értékeket vehet fel. Az egyes eloszlásokat nevezzük mikroállapotoknak, amelyek közül az valósul meg, amelyik a lehető legnagyobb számú kombinációban jöhet létre.

A mikroállapotok számához kapcsolódik az entrópia fogalma, ami arányos ennek a számnak a logaritmusával. Az arányossági tényező az R általános gázállandó. Ugyanez a gázállandó szerepel az ideális gáz nyomása (p), térfogata (V) és a hőmérséklet (T) közötti összefüggésben: p·V = R·T. Azokban az állapotokban, amelyek kisebb számban valósulhatnak meg, és így kisebb az entrópiájuk, mindig van bizonyos fokú rendezettség, ezért az entrópia növekedésre vezető folyamatok a rendezetlenség fokát növelik meg.

Szokás még az entrópiát az információval is összekapcsolni. A rendezett mozgást jóval kevesebb információ segítségével ismerhetjük meg, ha viszont nagyon nagy a lehetséges állapotok száma, akkor nagyon sok információt kell összegyűjtenünk, ha a nagyszámú molekula mozgásának teljes leírására törekszünk. Ebben az értelmezésben az entrópia a rendszer állapotának meghatározásához szükséges információ alapján definiálható.

Mi tartja össze a csillagokat és a bolygókat?

Szükségünk van még egy további lépésre, hogy eljussunk az evolúció fogalmához. Az entrópia úgynevezett extenzív mennyiség, amely a teljes rendszerre vonatkozik. A mikroállapotok révén azonban eljuthatunk egy lokális értelmezéshez is. Ha valamilyen V térfogatban N számú részecske, atom vagy molekula van, akkor ez meghatározza a komponensek átlagos távolságát.

De mekkora annak a valószínűsége, hogy két részecske éppen r távolságban van egymástól, ha ez a távolság kisebb az átlagos értéknél? Ennek valószínűsége arányos az r sugarú gömb felületével, azaz r²-tel. Ezáltal a részecskék térbeli eloszlásához rendelhetünk egy lokális entrópiát, amelyik a log(r²)=2log(r) kifejezéssel lesz arányos. Minél kisebb ez a távolság, annál kevésbé valószínű, hogy a véletlenszerű eloszlásban két részecske éppen ekkora távolságban legyen egymástól.

A részecskék között azonban különböző típusú vonzóerő léphet fel, ami kötött állapotot hozhat létre, ha a távolság kicsi. Például protonokban, neutronokban és más elemi részecskékben két vagy három kvark között gluonok közvetítik a vonzást, a protonokat és a neutronokat a magerők egyesítik atommagokká, Az atomok a pozitív töltésű atommagból és elektronokból állnak, ahol az elektromos töltések közötti Coulomb-kölcsönhatás játszik szerepet, de az atomok is egyesülhetnek molekulákká az elektronok által létrehozott kémiai kötések által. A molekulák között is létrejön vonzó kölcsönhatás szilárd testeket létrehozva, a nagy tömegű csillagokat, bolygókat és más égi objektumokat pedig a gravitáció tartja össze.

A vonzó kölcsönhatások közös vonása, hogy annál erősebbek, minél kisebb a távolság az objektumok között. Van azonban egy kvantumfizikai törvény, amely megakadályozza a teljes összeolvadást, nevezetesen a bizonytalansági reláció. Ennek egyik megnyilvánulása a pozíció és az impulzus közötti kapcsolat: minél közelebb kerül egymáshoz két objektum, annál bizonytalanabbá válik az impulzus.

A bizonytalanság mértékét fejezi ki a h Planck állandó, amelyik a kvantumos tulajdonságok alapköve. A kinetikus energia négyzetesen függ az impulzustól, amíg elhanyagolhatjuk a relativisztikus hatást. Ha viszont a relativisztikus effektusok fontosak, már bonyolultabb az összefüggés, de az impulzusnál ekkor is gyorsabban nő a kinetikus energia. Ez magyarázza, hogy a negatív töltésű elektront nem nyelheti el a pozitív töltésű atommag, noha nulla távolságban lenne a legkisebb a potenciális energia (határértékben negatív végtelen lenne!): kis távolságokban a potenciális energia csökkenését meghaladja a bizonytalansági elvből következő kinetikus energianövekedés.

Emiatt kötött állapotban az elektron az atommagtól számítva véges távolságban végzi mozgását; voltaképen ez határozza meg, hogy milyen nagy az atom és az atomokból felépülő molekula. Az entrópia viszont azért nem vehet fel végtelenül nagy negatív értéket, mert az r = 0 határeset nem valósul meg, és így a log(r) kifejezés mindig véges marad. Innen indulunk el a következő részben, hogy kapcsolatot keressünk az entrópia és az evolúció között.

A szerző a BME és az ELTE címzetes egyetemi tanára.

link Forrás