Az előző két méricskélős feladatnak és azok különféle verzióinak megoldásai következnek. A 8. feladványban minél kevesebb flaska felhasználásával kellett elosztani két egyenlő részre a vodkát. A hosszadalmas megfogalmazás azt volt hivatott leírni, hogy nagyjából bármilyen súlyú és térfogatú flaska rendelkezésre áll, de pontosan egyiknek sem tudjuk a paramétereit.

A feladat nagyon egyszerűen megoldható három flaskával, beleértve azt a flaskát is, amiben a vodka eredetileg van. Tegyünk fel a mérleg két oldalára egy-egy üres flaskát, és a könnyebbikbe öntsünk annyi vodkát, hogy a mérleg egyensúlyba kerüljön! Ehhez természetesen olyan flaskák kellenek, hogy a flaskák közti súlykülönbség kiegyensúlyozásához legyen elegendő vodka, és az ne csorduljon ki a könnyebbik flaskából, de a feladat feltételei szerint tudunk ilyen flaskákat választani.

Ezután ezt a mennyiséget félre kell tölteni, és az összes maradék vodkát kitölteni az előző két flaskába úgy, hogy azok megint egyensúlyba kerüljenek. Annak, hogy ezt meg tudjuk tenni, megint csak vannak feltételei, de erre még visszatérünk. A lényeg, hogy a kiegyensúlyozás után a nehezebb flaskában pont annyival kevesebb vodka lesz, mint amennyit félretettünk az első mérés során, azaz a két flaska súlykülönbségének megfelelő vodkával lesz azon az oldalon kevesebb. A félretett vodkát tehát egyszerűen hozzá kell tölteni, vagy a félretett flaskával együtt odaadni annak, aki a mérlegen lévők közül a kevesebb vodkát trartalmazó flaskát kapja. Ezzel be is fejeztük az osztozkodást.

Rendben, de mik a feltételek?

Térjünk még egy picit vissza arra, hogy pontosan milyen feltételek esetén lehet mindezt végigcsinálni! Legyen a vodkát eredetileg tartalmazó flaska tömege és térfogata M1 és V1 rendre, a másik két flaska tömegei és térfogatai pedig M2 < M3 és V2, V3 rendre. Legyen továbbá a vodka tömege és térfogata M0 és V0 < V1. Vegyük sorra a további feltételeket! Az első mérést, mint már korábban megfogalmaztuk, akkor tudjuk elvégezni, ha M3-M2 < M0, továbbá V2 > V0·(M3-M2)/M0.

Ezután a kimért M3-M2 súlyú és V0·(M3-M2)/M0 térfogatú vodkát félre kéne tölteni, de mivel ehhez nem akarunk negyedik flaskát használni, ezért azt kell csinálnunk, hogy az eredeti flaskában maradt vodkát áttöltjük a még üres flaskába, és ezt meg a helyére töltjük. Ennek a feltétele, hogy a maradék M0-(M3-M2) beleférjen a V3 űrmértékű flaskába, azaz V3 > (M0-(M3-M2))·(V0/M0). A kimért vodka visszatöltésének az eredeti flaskába nincsen feltétele, hiszen abban a flaskában eredetileg több is elfért.

A második méréshez az szükségeltetik, hogy a maradék M0+M2-M3 vodka még mindig legyen elegendő a flaskák súlykülönbségének kompenzálásához, azaz M3-M2 < M0+M2-M3; továbbá az, hogy egyik flaskából se csorduljon ki a vodka. Összefoglalva azt látjuk, hogy olyan flaskákat kell választanunk, melyek súlykülönbsége a vodka felének súlyánál kisebb, V2 és V3 térfogataik pedig legyenek elegendően nagyok, például legalább V0, azaz a vodka teljes térfogata, akkor biztos nem tud soha kicsordulni.

Három részre osztás

Vegyük észre, hogy a két részre osztásnál van egy macerás lépés, ami a gyakorlatban időigényes lehet! Az első mérésnél apránként töltjük a vodkát egy harmadik flaskából a mérleg egyik serpenyőjébe, amíg az egyensúlyba nem billen. A második mérésnél azonban a maradék vodkát maradék nélkül kell a mérleg két serpenyőjében lévő flaskák között elosztani, vagyis az egyensúly eléréséig a mérleg egyik serpenyőjében lévő flaskából kell a másik oldalon lévő flaskába öntözgetni apránként. Ez azzal jár, hogy minden egyes lépésben le kell vennünk az egyik flaskát, kicsit átönteni belőle, majd visszatenni a helyére, és figyelni a mérleget, hogy elbillent-e, vagy sem. Ha azonban ez a művelet megengedett, akkor ettől elviekben nem különbözik a három részre osztás sem, csak még időigényesebb.

Követhetjük a két részre osztás sémáját, csak több flaskára lesz szükség. Veszünk három flaskát, amikbe belefér a vodka, és a páronkénti súlykülönbségeik kicsik. Megfelelő mennyiségű vodkával kimérjük a legnagyobb és a legkisebb, illetve a középső és legkisebb súlyú flaska közti súlykülönbségeket, és félrerakjuk ezeket egy-egy flaskában. Ezután a három flaska között elosztjuk a maradék vodkát úgy, hogy páronként egyensúlyban legyenek, flaskástól. Ezt úgy csináljuk, hogy kiegyensúlyozunk két flaskát, majd ezek közül az egyiket a harmadikkal, majd újra az első kettőt, és így tovább, felváltva. A felváltva történő páronkénti kiegyensúlyozásokkal fokozatosan tartunk a közös egyensúlyhoz, és egy idő után elérjük a mérleg mérési pontosságát, amikor bármely kettőre egyensúlyban lesz a mérleg. A legvégén a félretett vodkamennyiségekkel kiegészítve a három flaskát pont három egyenlő részt kaphatunk.

Osztozkodás homokkal

A 9. feladvány megoldása szintén egyszerű, ha van akármennyi homok, és a flaskák mindegyikébe belefér a teljes vodkamennyiség. Ekkor ugyanis a vodkát az egyik, illetve a másik flaskában is tárolhatjuk ideiglenesen, miközben a másik üres flaskát önmagában ki tudjuk egyensúlyozni homokkal. Ha ezeket kimértük, akkor az egyik serpenyőbe az egyik flaskát tesszük és a másik flaskával megegyező súlyú homokkupacot, míg a másik serpenyőbe a másik flaskát és az elsővel megegyező súlyú homokkupacot. Így mindkét serpenyőben azonos lesz a flaska+homok súlya, tehát ha a mérleget a vodka elosztásával egyensúlyba tudjuk hozni, akkor mindkét oldalon egyenlő mennyiségű vodka lesz.

Mindehez az kellett, hogy a két flaska súlyával megegyező homokkupacokat félretegyünk, azaz M1+M2 tömegű homokra volt szükség. Valójában azonban elegendő lenne egy M2-M1 tömegű homokkupac is, ha M2 > M1, hiszen ennyit kéne a kisebb M1 súlyú flaska mellé tenni a serpenyőbe, ha a másik oldalra nem tennénk semmi homokot, csak a flaskát. Ezt könnyen meg lehet csinálni, ha van összesen legalább M2 tömegű homok, mert akkor ezzel kiegyensúlyozzuk az M2 tömegű flaskát, majd ebből a homokból felhasználva egyensúlyozzuk ki a kisebb M1 tömegű flaskát, így visszamarad M2-M1 tömegű homok az első kupacból.

De vajon elképzelhető-e, hogy még ennél kevesebb homok is elegendő lehet?

Az egyszerűség kedvéért előbb állapítsuk meg, hogy melyik flaska a nehezebb üresen, ez ugyanis nem egyértelmű, hiszen a vodkának mindig benne kell lennie az egyikben, és most kevesebb homokunk van annál, hogy a nehezebb flaskát önmagában lemérjük.

Tegyük fel az M1 tömegű flaskában a vodkát az egyik oldalra, és tegyük fel az M2 tömegű flaskát a másik oldalra! Ha az M2 felé billen a mérleg, vagyis M2 üresen nehezebb, mint M1 vodkával teli, akkor M2 > M1, egyértelműen. Ha a mérleg a másik oldalra billen, akkor M2 mellé felrakunk annyi homokot, hogy egyensúlyba kerüljön: ez éppen M1+M0-M2 tömegű homokot jelent. Ha M1 > M2, akkor a feladat feltételei szerint rendelkezésre áll ennyi homok, mert M0 < M2 = min(M1,M2), tehát M1+M0-M2 < M1 = max(M1,M2). Ha M1 < M2, akkor is igaz, hogy M1+M0-M2 < max(M1,M2) = M2, mert most M0 < M1 = min(M1,M2), tehát M0+M1 < M1+M2 < 2·M2, és mindkét oldalból levonva M2-t megkapjuk a kívánt feltételt.

Ezek után feltehetjük az általánosság megszorítása nélkül, hogy M1 > M2, hiszen ez csak elnevezés kérdése. Egy lehetséges megoldás az alábbi. Első lépésben feltesszük az M0 tömegű vodkát az M1 tömegű flaskában az egyik oldalra, és a másik M2 tömegű flaskát üresen a másik oldalra, és kiegyensúlyozzuk M1+M0-M2 < M1 tömegű homokkal, ahogy azt már korábban leírtuk. A kiegyensúlyozáshoz felhasznált M1+M0-M2 > 0 tömegű homokot félretesszük. Ezután a vodkát áttöltjük a másik flaskába a mérleg másik oldalára, és megnézzük, hogy homok nélkül merre billen a mérleg. Két eset lehetséges: M1 < M2+M0, vagy M1 > M2+M0.

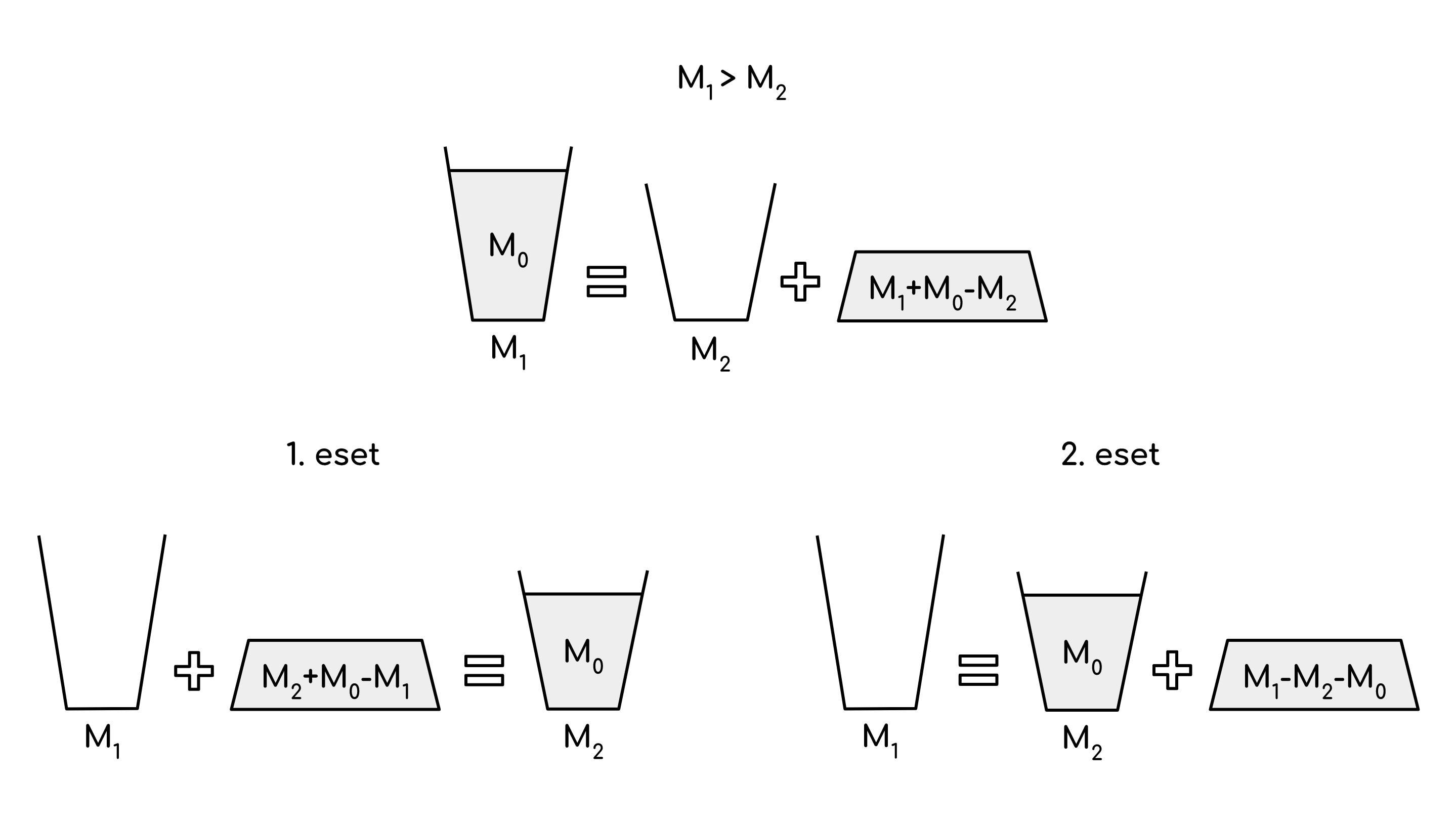
Nézzük az első esetet! Ebben az esetben az üres M1 tömegű flaska mellé M2+M0-M1 tömegű homokot kéne feltenni, hogy egyensúlyba kerüljön a mérleg. Mármost M1+M0-M2 = M2+M0-M1+2·(M1-M2), tehát a félretett homok éppen 2·(M1-M2) tömeggel több, mint amire a kiegyensúlyozáshoz szükségünk van, vagyis a félretett homokból elvehetjük a kiegyensúlyozáshoz szükséges mennyiséget. Ekkor marad 2·(M1-M2) > 0 tömegű homok félretéve, ami pont kétszerese annak a súlykülönbségnek, aminek a kimérésére hajtunk. Ezt egyszerűen el tudjuk felezni, ha mindent leveszünk a mérlegről, és most csak ezt a homokmennyiséget tesszük fel úgy a mérleg két oldalára, hogy a mérleg egyensúlyban legyen.

Jó, de mi van a második esetben?

A második esetben a mérleg másik oldalára M2+M0 mellé kéne M1-M2-M0 > 0 tömegű homokot tenni, hogy az egyensúlyba kerüljön M1-el. Ez a félretett M1-M2+M0 tömegű homoknál 2·M0-val kevesebb. Ha tehát a félretett homokot használjuk fel a kiegyensúlyozáshoz, akkor éppen a vodka súlyának kétszerese marad félretéve, továbbá lesz még M1-M2-M0 tömegű homok is kiporciózva. Az előbbit megfelezve a mérleg segítségével kapunk két M0 tömegű porciót, amiből az egyiket hozzátéve az M1-M2-M0 tömegű porcióhoz megkapjuk azt az M1-M2 súlykülönbséget, amire hajtottunk.

Megjegyezzük, hogy léteznek ennél még egyszerűbb módszerek is esetszétválasztás nélkül, ha a homokkal nem feltétlenül úgy egyensúlyozzuk ki a mérleget egy mérés során, hogy az egyik serpenyőbe töltjük apránként kívülről, hanem az egyik serpenyőből átlapátolhatunk a másikba apránként, az egyensúly beálltáig. Például kezdhetjük ugyanúgy a mérést, ahogy a fenti eljárásban, de az első mérés során a kiegyensúlyozásra használt M1+M0-M2 tömegű homokkupacot hagyjuk teljes egészében a mérleg jobb oldalán, a vodkát pedig öntsük át szintén a jobb oldalra az M2 tömegű üres flaskába. Ha az M1 tömegű flaskát a bal oldalon hagyjuk, akkor az M1+M0-M2 tömegű homokkupacból pont M0 tömegűt kell átlapátolni a bal oldalra, hogy a mérleg egyensúlyba kerüljön, tehát sikerült a vodka tömegét viszonylag gyorsan és egyszerűen kimérnünk homokból, ahonnan a befejezést már az olvasóra bízzuk.

Végül megemlítjük, hogy akkor is van lehetőség a felezésre, ha a vodka M0 tömege a két flaska tömege közé esik. Ha ugyanis el akarunk tárolni valamennyi homokot, de egyúttal szükség lenne a homokra további független mérések elvégzéséhez, akkor azt a trükköt alkalmazhatjuk, hogy a teljes homokkupac eltárolása helyett elkezdjük azt felezgetni, és csak egy nagyon kis részét tároljuk el, emlékezve arra, hogy az hányadrésze az eredetinek. Esetünkben ez természetesen mindig egy kettő-hatvány lesz. Ezt a trükköt megfelelő módon alkalmazva el tudjuk tárolni az M0, M1 és M2 valamilyen független kombinációinak fenti értelemben vett részleteit, majd azok segítségével végső soron elő tudjuk állítani a flaskák súlykülönbségét.

Az üveg alján megmaradó vodka

Végül pedig nézzük azt az esetet, amikor a másik flaskába nem fér bele az összes vodka! Ekkor a vodka egy kis része mindig benne kell maradjon az eredeti flaskában. Nyugodtan feltételezhetjük, hogy ez a kis rész mindig ugyanaz az üveg alján, és valójában nincs módunkban megkülönböztetni, hogy ez a rész a flaska része vagy a vodka része. Precízebben fogalmazva: tegyük fel, hogy valamilyen módszerrel meg lehet felezni a vodkát, de akkor ugyanezzel a módszerrel meg kellenetudni felezni a vodkát ugyanazzal a végeredménnyel – akkor is, ha az üveg alján lévő vodka nincs, hanem helyette annyival nehezebb a flaska. De a két esetnek nem lehet ugyanaz a végeredménye, mert eltérő a vodka mennyisége, tehát ilyen módszer nem létezhet.