A parázsbogár-origamival kapcsolatban az volt az alap feladat, hogy felhasználva az információt, miszerint van neki kilenc darab 3 hüvelyk hosszú nyúlványa (lábak, potroh és szárnyak) továbbá 32 darab 1 hüvelyk hosszú szőrszála a fésűs csápján, mutassuk meg, hogy a négyzet alakú papírlapnak, amiből készült, legalább 12 hüvelyk az oldalhossza.

A korábbi írásomból már kiderülhetett, hogy a feladat átfogalmazható körpakolási problémává. Ahogy azt az illusztráció is szemléltette, minden vékony nyúlványra igaz, hogy a végpontja körül egy a nyúlvány hosszával megegyező sugarú kört rajzolva a (kihajtogatott) papírlapon egy olyan területet határolunk körbe, melynek minden pontja biztosan a nyúlvány része lesz. Attól függően, hogy a nyúlvány csúcsa hova esik a papírlapon, ez a terület lehet például félkör, ha a papír szélére esik, vagy lehet negyedkör is, ha épp a sarokra esik. A papír bármelyik pontja azonban legfeljebb csak egy nyúlvány része lehet, így ezek a körök nem fedhetik át egymást. A kérdés tehát az, hogy egy 12 hüvelyk oldalhosszúságú négyzetbe elhelyezhetők-e úgy a körök (kilenc darab 3 hüvelyk sugarú és 32 darab 1 hüvelyk sugarú) középpontjai, hogy a körök sehol ne fedjék át egymást.

Mármost egy kör nyilvánvalóan akkor foglal a legkevesebb helyet a négyzetből, ha a középpontja épp egy sarokra esik, ekkor csak egy negyedkörnyi terület foglal. Egy sarkot pedig csak egy kör foglalhat el ilyen módon. Ha a sarkok már foglaltak, akkor a lehető legkevesebb helyet úgy foglalhatnak a körök, ha a középpontjuk a papír szélére esik, ekkor a papírra eső részek félkörök lesznek. Próbáljunk becslést adni arra, hogy a szóban forgó körök legalább mekkora területet foglalnak el összesen a négyzet alakú papírból.

Mivel csak négy sarok van, ezért a sarkokra legfeljebb négy kör középpontja helyezhető, az összes többi legalább félkörnyi területet kell fogaljon. Valójában négy híjával se tudnánk az összeset a papír szélére rakni, mert nincs olyan nagy kerülete a négyzetnek, hogy annyi félkör elférjen rajta, de nekünk ez a durva becslés is elegendő lesz. A legkisebb lefedett összterületet akkor kapjuk, ha a sarokra nagy körök negyedköreit helyezzük, így az összterületre azt kapjuk, hogy legalább 4 nagy negyedkör + 5 nagy félkör + 32 kis félkör, ami hüvelyk négyzetben mérve (3^2) π + (5/2) × (3^2) π + 16 π = 47,5 π ≈ 149,2. Ez pedig nagyobb, mint 12 × 12 = 144, tehát a körök semmilyen elrendezésben nem férhetnek bele egy 12 hüvelyk oldalhosszú négyzetbe.

Ennél persze sokkal jobb becslést is lehet adni, mert fentebb csak azt vizsgáltuk nagyon durván, hogy területileg a körök beleférnek-e a négyzetbe, de tudjuk, hogy a körök nem tudnák hézagmentesen kitölteni a papírt, tehát szükségszerűen kell legyenek körök által nem lefedett területek is a körpakolás egy konkrét megvalósításában. Origamis szempontból persze más praktikus feltételeknek is meg kell felelni, például az egyes nyúlványokhoz tartozó körök egymáshoz képesti elhelyezkedése sem lehet tetszőleges, a szőrszálakat például érdemes egymás mellé rakni. Alább láthatjuk az alkotó által ténylegesen használt diagramot, amiből kiderül, hogy ő a szőrszálakat a papír szélére helyezte, és a nagy körök a belső tartományba kerültek, ezért 12 hüvelyknél lényegesen nagyobb, kb. 20 hüvelykes papírt volt, amit felhasznált. Jól látható azonban, hogy a körök így is elég szorosan helyezkednek el.

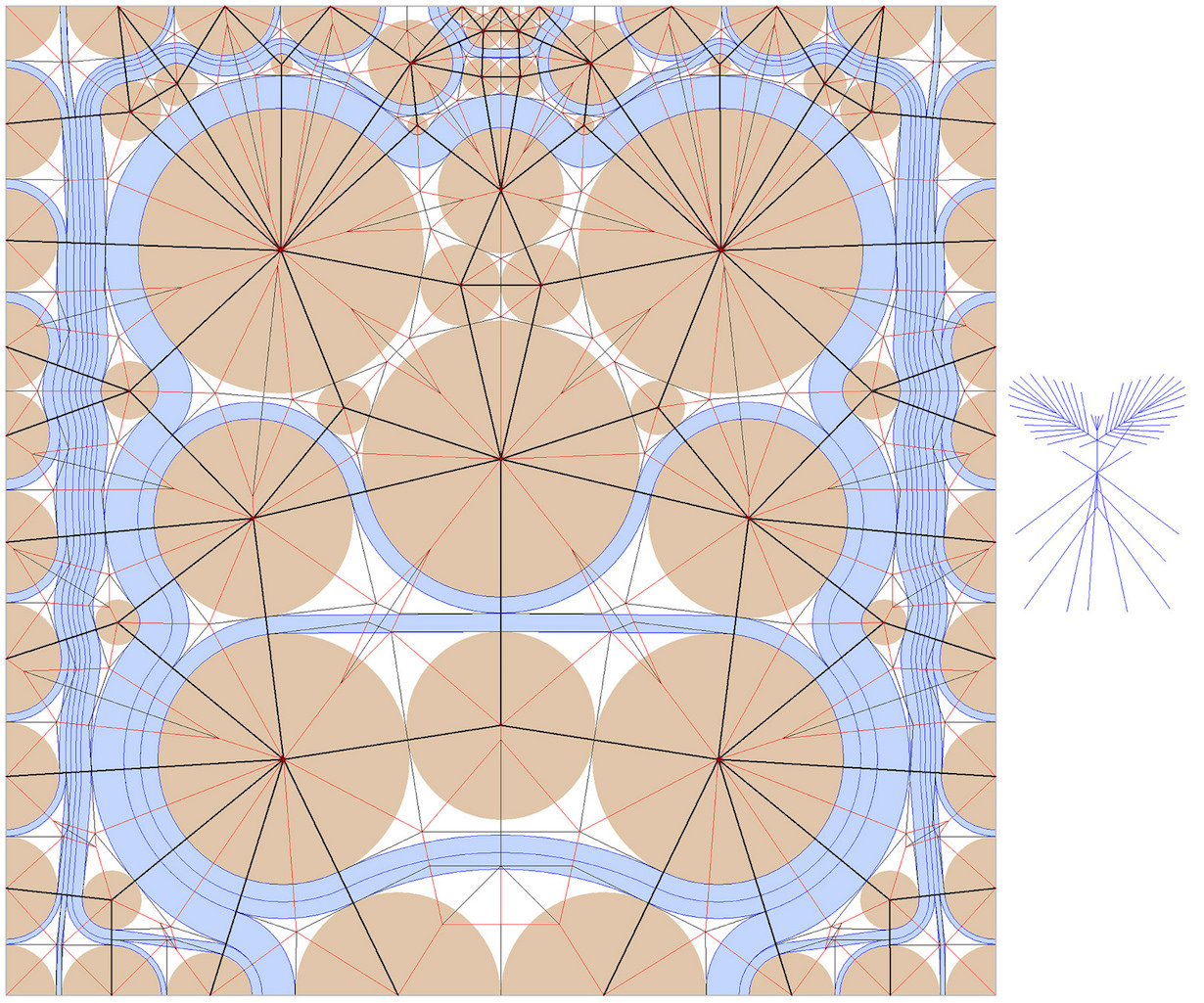
Megjegyzés: a diagramon több kört láthatunk, hiszen ott van még a tor, a fej és a szájnál még pici csáprágók, amikről a feladatban nem volt szó.