Hogyan segíthet az információelmélet abban, hogy megtaláljuk, milyen szavak tartoznak szorosabban össze egy hosszú szövegben (a mondatokon belül), és alkotnak úgynevezett kollokációt?

Korábban arról volt szó, hogy például a bakot lő szókapcsolatot lefülelhetjük: kimutathatjuk, hogy szoros kapcsolatot alkot, ha megvizsgáljuk a bakot szó előfordulásait, meg a lő szó előfordulásait, meg a kettőt együtt. Itt az előfordulás szót nagyon egyszerűen értjük: hányszor van az, hogy két egymás melletti szóból az első a bakot szó (és hányszor más); hányszor a második a lő szó (és hányszor más), végül hányszor éppen a bakot lő a két szó (és hányszor más). Ennél sokkal finomabban is jellemezhetnénk az előfordulásaikat, de erről majd egy másik részben próbálunk elgondolkozni.

Akkor arra jutottunk, hogy az entrópia fogalma szépen és tisztán árulkodik a két szó összefüggéséről. Az entrópia egy rendszer bonyolultságát, kiszámíthatatlanságát, „rendetlenségét” fejezi ki. Ezt egy képzeletbeli teknőccel illusztráltam, egy képzeletbeli kísérletsorozatban, ahol szépen számszerűsíteni tudtuk, hogy mennyire szeszélyes a teknőc, vagy fordítva, mennyire kiszámítható, unalmas a viselkedése. A bakot lő esetében ez a számítás úgy használható, hogy ha a két szó előfordulásait egy nagyon hosszú szövegben (úgynevezett korpuszban) egy-egy kísérletsorozatnak tekintjük, akkor kiszámolhatjuk, hogy mennyire kiszámíthatatlan az előfordulásuk. Nyilván nagyon, tehát nagy entrópia-értékeket kapunk, de nem is ez az érdekes, hanem az, hogy mennyivel kisebb ennél annak a kísérletsorozatnak az entrópiája, amikor a két szó, a bakot és a lő együttes előfordulását vizsgáljuk. Tehát a kérdés az, hogy mennyi információt nyerünk, ha együtt nézzük a két szó előfordulását, vagyis végső soron egyszerű kivonásról van szó:

H_bakot + H_lő – H_{bakot lő},

ahol H_x az x szó előfordulásának az entrópiája. Megbeszéltük, hogy az entrópia egyfajta átlag, ami azt fejezi ki, hogy a kísérletsorozaton belül egy-egy kísérlet átlagosan mennyi információt hordoz a rendszer viselkedéséről. Magát a fenti különbséget pedig úgy neveztük, hogy a bakot és a lő előfordulásainak kölcsönös információja (KI, mutual information). Mindezt megpróbáltam a lehető legjobban leegyszerűsítve elmondani, hogy könnyebb legyen később mindenféle irányokba továbblépni.

Az egyik továbblépési irány majd az lesz, egyszer később, hogy a szavak előfordulását bonyolultabb módon fogjuk fel, nem egyszerűen úgy, hogy az a bizonyos szó szerepel-e egy helyen, vagy egy másik. Most egy másik továbblépési irányon fogunk elgondolkozni, mégpedig azon, hogy mit tehetünk azzal a problémával, amit a korábbi részben már említettem, hogy a kölcsönös információ mérése sok ún. hamis pozitív eredményt ad, vagyis hajlamos kollokációnak minősíteni olyan szópárokat, amik gyakran fordulnak elő egymás mellett, de mégsem tartoznak olyan szorosan össze, mint mondjuk a bakotés a lő. Ilyen hamis pozitív szópár volt például a tudatjuk és a mindazokkal. Ezeknek azért nagy a KI-juk, mert gyakran fordulnak elő egymás mellett gyászjelentésekben, és ez a két szó aránytalanul sokszor fordul elő éppen gyászjelentésekben.

Sajnos ennek a fajta hamis pozitív eredménynek a kiküszöbölésére nem sok esélyünk van. Mert még ha tudnánk is valahonnan, hogy a korpuszban melyik szövegrész gyászjelentés, és melyik nem, akkor sem lenne okunk ezen az alapon kizárni a kollokációk közül azt, hogy tudatjuk mindazokkal, mert igenis vannak kollokációk, amik egy bizonyos szövegfajtára jellemzőek (mondjuk inkább meteorológiai jelentésekben fordul elő a változó felhőzet, de ettől még lehet kollokáció). A sok hamis pozitív eredmény az egyik oka annak, hogy a gyakorlatban a kollokációk keresésében nem a kölcsönös információt használják, hanem egy másik mutatót, ami ebből a szempontból kedvezőbben viselkedik. (A másik oka az, amit szintén említettem korábban, hogy rettentő bonyolult és időigényes számításokra van szükség ahhoz, hogy megállapítsuk, mikor szignifikáns egy kiszámított KI.)

Egyedi kölcsönös információ

Azt a bizonyos másik mérőszámot, amit a kollokációk keresésénél a leggyakrabban használnak, én egyedi kölcsönös információnak (EKI) fordítom magyarra (angolul pointwise mutual information a neve). Fogalmilag ez a mérőszám nem annyira az információelméleten, hanem inkább a valószínűség-számításon alapul, bár a kettő valahol összeér egymással. És bár maga az egyedi kölcsönös információ viszonylag egyszerű fogalom, én ragaszkodom hozzá, hogy előbb-utóbb lássuk be együtt, hogy miért éppen úgy kell kiszámítani, ahogy.

Mi köze a valószínűségeknek a korpuszokban való keresgéléshez meg a kollokációkhoz? Az emberiségnek sajnos nagyon rosszak a valószínűségekre vonatkozó intuíciói, de azt talán mindenki gyorsan belátja, hogy a valószínűségek határértékek, vagyis úgy lehet mérni őket, ha nagyon sokszor megismétlünk egy kísérletet. Vegyük a legegyszerűbb példát, a pénzfeldobást. Mindenki érzi, hogy ha a fej és az írás valószínűsége egyforma, akkor az a valószínűség „fifti-fifti”, vagyis 50 százalék, és ez azzal jár, hogy minél többször dobjuk fel a pénzt, annál közelebb lesz 50 százalékhoz (vagyis a 0,5-höz) a fejek (és az írások) számának aránya az összes dobás számához viszonyítva.

Mellékes, de elmondom, hogy miért írtam, hogy rosszak a valószínűségekre vonatkozó intuícióink. Ha például úgy tesszük fel a kérdést, hogy mennyi a valószínűsége annak, hogy n pénzfeldobásból pontosan n/2 alkalommal lesz fej az eredmény, azt semennyire sem tudjuk megbecsülni. És sokan elcsodálkoznak azon, hogy ez a valószínűség nagyon gyorsan csökken (nemhogy nőne), ahogy az n-t növeljük, annak ellenére, hogy a fejek arányának pont 1/2 az elvileg várható értéke. És akkor még nem is beszéltünk arról, amikor eleve nem egyforma valószínűségű eseményekkel van dolgunk.

Szóval ha megszámoljuk, hogy egy nagyon nagy korpuszban hányszor fordul elő egy bizonyos szó (körülbelül ez a legegyszerűbb dolog, amit egy korpuszban vizsgálhatunk), vagyis a szó gyakoriságáról beszélünk, akkor azt felfoghatjuk úgy, mintha rengeteg kísérletet végeznénk (minden egyes szó megjelenését egy-egy kísérletnek tekintjük). Ezért a szó relatív gyakoriságát (vagyis azt, hogy a korpusz teljes hosszához képest hányszor találkozunk éppen ezzel a szóval) úgy tekinthetjük, hogy az elég jól közelíti az illető szó előfordulásának valószínűségét. Persze mindig tudnunk kell, hogy a megfigyelt relatív gyakoriság csak közelítése a valószínűségének, de elég jó közelítése ahhoz, hogy úgy számoljunk vele, mintha valószínűség lenne, és ugyanúgy jelöljük is. Például ha P_szó(bakot) jelöli annak az eseménynek a valószínűségét, hogy a korpuszból egy véletlenszerűen választott szó éppen a bakot, akkor az egyszerűség kedvéért a bakot szó relatív gyakoriságát is jelölhetjük ugyanígy, ha elég nagy a korpuszunk.

Ahogy a KI, az EKI is azt veszi alapul, hogy milyen gyakran fordul elő külön-külön két szó, és milyen gyakran egymás mellett. Olyan mérőszámról van szó, ami számtalan statisztikai hipotézis-vizsgálatnak az alapját képezi, és aminek az a lényege, hogy egy megfigyelt valószínűségi becslést (nevezzük M-nek) viszonyítunk egy elvi valószínűséghez (egy nullhipotézishez, nevezzük E-nek), és a kettő arányának a logaritmusát vesszük: log(M/E).

Mi lenne egy kollokáció-keresésnél a megfigyelt valószínűségi becslés, és mi lenne a nullhipotézis? A megfigyelt becslés nyilván az, hogy hányszor fordul elő egymás mellett két szó (mondjuk a bakot és a lő) az egész korpusz hosszához (a benne levő szópárak számához) képest, vagyis M = P_szópár(bakot lő). A nullhipotézis pedig az, hogy a két szó előfordulása független egymástól, vagyis hogy az együttes előfordulásuk valószínűsége nem más, mint a külön-külön előfordulásuk valószínűségének a szorzata: E = P_szó(bakot) × P_szó(lő). (A rend kedvéért az egyszerű szóelőfordulások helyett azt számolom, hogy hányszor fordul elő a bakot egy szópár első elemeként, és hányszor a lő egy szópár második elemeként, de a felírásban ezzel a részlettel nem bajlódom.) Az egyedi kölcsönös információ kiszámításának módja tehát ez:

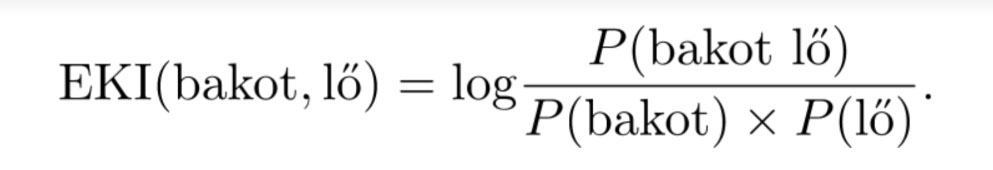
Bár sokan tudják, beszéljük meg gyorsan, hogy ha két esemény független egymástól, akkor miért éppen a külön-külön mért valószínűségük szorzata az együttes valószínűségük. Ezt nagyon könnyű belátni. Vegyük megint a pénzfeldobást. Ennek az eseménynek két lehetséges kimenetele lehet, egyforma valószínűségűek (fifti-fifti, vagyis 0,5): fej vagy írás. Ha kétszer dobjuk fel a pénzdarabot, annak négyféle kimenetele lehet (fej–fej, fej–írás, írás–fej, írás–írás), és hogy a két dobás független egymástól, az éppen azt jelenti, hogy ennek a négyféle kimenetelnek egyforma a valószínűsége. Tehát hosszú távon (határértékként) mindegyik az esetek 1/4 részében következik be, ami 25%-ot, vagyis 0,25 valószínűséget jelent. Nem véletlen, hogy ez a 0,25 éppen a két esemény külön-külön valószínűségének a szorzata (0,5 × 0,5 = 0,25), hiszen a kimenetelek száma is a két esemény kimeneteleinek a szorzata.

A kétféle mérőszám összehasonlítása

Ahogy említettem, az egyedi kölcsönös információ többek között annak köszönheti a népszerűségét, hogy a speciális esete egy olyan mérőszámnak, amit a statisztikában igen gyakran használnak, és ezért például könnyen meghatározható, hogy (legalábbis közelítőleg) mennyire szignifikáns egy-egy ilyen érték. Ennek ellenére köztudott, hogy sem az egyedi, sem a sima kölcsönös információ nem ad kielégítő eredményeket (mind a kettő sok szókapcsolatot kollokációnak értékel, amit nem érzünk annak, és sokat nem, amit igen).

Például nagyon egyszerű belátni, hogy az EKI-nek nagyon természetellenes tulajdonsága, hogy a legnagyobb értékeket az olyan szókapcsolatok kapják, amelyik csak egyetlen egyszer fordul elő a korpuszban (annak az esetében ugyanis az M/E hányadosban a nevező a számláló négyzete, tehát az érték fordítottan arányos a szókapcsolat gyakoriságával). Így feltétlenül a kollokációk közé kerülnek az olyan elírások, ahol tévedésből vagy rossz helyre írt valaki betűközt (zsolo zsmázik vagy vacsor aután). De ez nem jelenti azt, hogy minél ritkább egy kollokáció, annál inkább megtaláljuk. A sima kölcsönös információ más irányban hajlamos tévedni, például sokszor magas értéket kapnak olyan szópárok, amik gyakran fordulnak elő, de nem azért, mert kollokációk, hanem mert ez a mérőszám meg egy kicsit aránytalanul előnyben részesíti a gyakoriságot.

Ezek miatt az okok miatt a kétféle mércének mindenféle változatát, módosítását szokták használni a kollokációk kinyerésére, és elmondhatjuk, hogy a problémának még nincs megnyugtató megoldása. Ráadásul a céljainktól függően mást és mást érthetünk a kollokáción, ezért nem is lehet pontosan megmondani, hogy mi lenne a tökéletes és univerzális megoldás.

A lehetséges változatok tárgyalása helyett inkább néhány érdekes adattal zárom ezt a részt. Ezúttal az egész Magyar Nemzeti Szövegtár korpuszát használtam (nem pedig csak egy belőle származó gyűjtést). Ez a korpusz regisztráció után szabadon használható, és több mint egymilliárd szót tartalmaz. Az EKI legkisebb figyelemre érdemes (szignifikáns) értéke ebben az esetben valahol 7 körül van (kb. 7,88-nál éri el azt a szintet, ahol már csak öt ezrelék a valószínűsége, hogy amit megfigyeltünk, az a véletlen műve, és kb. ez 10,83-nál éri el az egy ezreléket).

Például a tipikus kollokációnak, a bakot lő szókapcsolatnak az EKI-je ennek a korpusznak az alapján 8,24, míg ha százalékban fejezzük ki a KI-t (vagyis azt számoljuk ki, hogy a mennyi információt nyerünk azzal, ha egyetlen rendszernek tekintjük a két szó előfordulását), akkor csak 0,12%-ot kapunk, ami elhanyagolható. Ezt az alacsony értéket az okozza, hogy a kölcsönös információban sokat számít a gyakoriság, márpedig a bakot lő (így, szó szerint, ebben az alakjában) csak 15-ször fordul elő az MNSZ-ben.

A tudatjuk mindazokkal pár EKI-je szintén 8,22, ami az elmondottak alapján nem meglepő; itt a kölcsönös információ 2,12%-os nyereséget mutat, ami nagyobb ugyan, mint a bakot lő 0,12%-a, de még mindig nagyon kevés. Azt viszont elmondhatjuk, hogy ebben az esetben a KI jobban teljesít, mert ezt a szópárt nem is akarnánk kollokációnak tekinteni.

A bakot lő-nél (legalábbis ennél az egyes szám harmadik személyű, jelen idejű alakjánál) sokkal gyakoribb állandósult szókapcsolat az egyik korábbi részben már említett csodák csodája, és ennek kollokáció-voltát az EKI (7,96) és a KI-nyereség (5,25%) egyaránt mutatni látszik, bár statisztikailag ezek valószínűleg még gyengék. Érdekes módon a korábban már szintén látott alapos gyanú és maró gúny kifejezéseket ebben a teljes, szűrés nélküli korpuszban az EKI nagyon enyhén mutatja kollokációnak (4,59, illetve 7,08), a KI viszont egyáltalán nem (nyereség 1% alatt). Ez megint azt is mutatja, hogy a KI nagyon érzékeny a korpusz méretére, és hogy érdemesebb valamilyen előzetesen megszűrt adatokra alkalmazni, például olyanokra, amiből a leggyakoribb szavakkal (a névelőkkel és hasonlókkal) nem számolunk.

Ezek után nem csodálkozhatunk azon, hogy a romokban hever kifejezést mindkét mérőszám elég egyértelműen kollokációnak minősíti (8,64, illetve 8,86%). Ez ugyanis sokkal gyakoribb, mint a bakot lő (863 előfordulás). Ellenőrzésképpen ránézhetünk olyan ritkább és gyakoribb szópárokra, amik mondattanilag összetartozó szavakból állnak, de nem kollokációk (majmot etet, kutyát etet, három majom), valamint olyanokra, amik gyakran egymás mellett előforduló szavak, de mondattanilag sem tartoznak össze (pl. szereti a). A három (sorrendben egyre gyakoribb) szópár esetén az EKI szépen csökken, de az elsőt a ritkasága miatt még enyhén kollokációnak minősíti (5,99, 3,67, illetve –0,4), míg a KI-nyereség mindegyiknél messze 1% alatt van, az össze nem tartozó szavaknál pedig az EKI megint enyhén negatív (–1,24), a KI-nyereség pedig megint elhanyagolható.

A szerző nyelvész, az MTA Nyelvtudományi Intézetének főmunkatársa.

link Forrás