A topológusok boroskancsóján keresztül próbáltam a topológiát egy kicsit közelebb hozni az olvasókhoz, nem tudom, ez mennyire sikerült. Igyekeztem rávilágítani kicsit szokatlan szemszögből a kint és bent fogalmára, volt szó továbbá felületekről és magasabb dimenziókról is a feladványban, remélem közérthető módon.

Elismerem, a topológia szemlélete furcsa lehet, mert nagyon tág műveleteket enged meg, ugyanakkor a matematika klasszikus ágainál sokkal érdekesebb lehet azok számára, akik a számokért nem annyira lelkesednek. A topológia kivételes területe a matematikának, hiszen nem szerepelnek benne közvetlenül számok, de még távolságok és szögek sem. A topológiában mindent szabadon el lehet deformálni, és ugyanaz a dolog végtelen sokféle alakot ölthet, aminek csak a képzeletünk szab határt. A topológia nem foglalkozik azzal, hogy hol, mi, mekkora, hanem azzal foglalkozik, hogy milyen, akármilyen szemszögből is nézzük, akárhogyan is torzítjuk vagy deformáljuk. A topológia a lehető legjobban az ideák világában van, hiszen a geometria, bár tökéletes idomokkal foglalkozik, azért azok a valóságra elég jól alkalmazhatók a gyakorlatban, végtelenül rugalmas és nyújtható anyag viszont nincs a fizikai világban. Ennek ellenére a topológia képes mégis a dolgok olyan leglényegét megragadni, ami még tökéletlen voltuk ellenére is mindig sajátjuk marad.

Ami a feladványt illeti, nem sok megoldást kaptam, feltehetőleg az értelmezés okozott sokaknak nehézséget. Ezúton is bátorítok mindenkit, hogy ha valami nem világos egy feladvánnyal kapcsolatban, nyugodtan lehet kérdezni. Az volt a kérdés, hogy az ábrán látható Klein-kancsó üvegfalának egymással összefüggő külső és belső felülete milyen felület valójában. Vagyis próbáljuk a felületet kicsomózni, ha kell, akár magasabb dimenziókba is kilépve. Segítségként meg volt adva néhány tipp, ami azt sugallta, hogy leginkább azt kellene eldönteni, hogy hány lyukat is tartalmaz ez a felület valójában. A kitűzésnél megadott ábrasorból az elsőt, ami csak egy lyukat tartalmaz, vagyis az úszógumi felületet, a továbbiakban tórusznak nevezzük.

A megoldáshoz segít, ha a felületet részekből rakjuk össze. Gondoljuk el azt, hogy a kancsót megtöltjük borral az üveg nyakának tövéig, vagyis bor tölti ki az üveg belsejét, egészen a világoskék körrel jelölt szintig. A bor által kitöltött térfogat körül fogja ölelni a kancsóba visszaforduló nyakat, ezért a bor (folytonos deformációktól eltekintve) egy tóruszt nedvesít meg belülről, amiből csak a nyak tövénél fog hiányozni egy kis darabka, aminek a világoskék kör a kerülete.

Ha a kancsót kivülről szemléljük, akkor az egy füles gömbhöz hasonlít, eltekintve a lyuktól az alján, amit a sárga kör határol. A külső felület tehát (deformációktól eltekintve) ugyancsak egy tórusz, amiből a sárga körnek a helyén hiányzik egy darabka. A fentebb említett belső tóruszt és a külső tóruszt a kancsó nyakának (ami egyben a füle is) belső felülete köti össze: ez egy cső, aminek egyik vége a világoskék kör, másik vége a sárga kör, és áthalad a fehér körön, ahol is a fehér kör az üvegcső belső kerületét jelöli. Ezzel megvan a felület összes darabja: a belső felület egy tórusz, a külső felület is egy tórusz, és a kettőt a kancsó fülének belsejében futó cső köti össze. A kancsó fülének külső felülete is egy cső, de az a külső tórusz része, azt tehát már beszámítottuk, a kancsó belsejében futó része meg a belső tóruszhoz tartozik, amit ugyancsak figyelembe vettünk már.

Összesítve tehát a kérdéses felület két tórusz, amik egy csővel össze vannak összekötve, ez tehát egy kétlyukú felület, egy ún. kétlyukú tórusz, ami az ábrasorban a második volt a lehetőségek közül. Csakhogy ez a felület össze van gubancolva, ugyanis a belső tórusz a külső tóruszban van benne, ráadásul úgy, hogy a belső tórusz körülöleli a két tóruszt összekötő csövet, továbbá ez a cső körülöleli a külső tórusz lyukát. Kicsit szemléletesebben az alábbi ábrán látszik a szituáció, ami tehát még nincsen kibogozva, csak olyan módon ábrázoltuk a szóban forgó felületet, hogy a tóruszok és az őket összekötő cső helyzete jobban látszódjék.

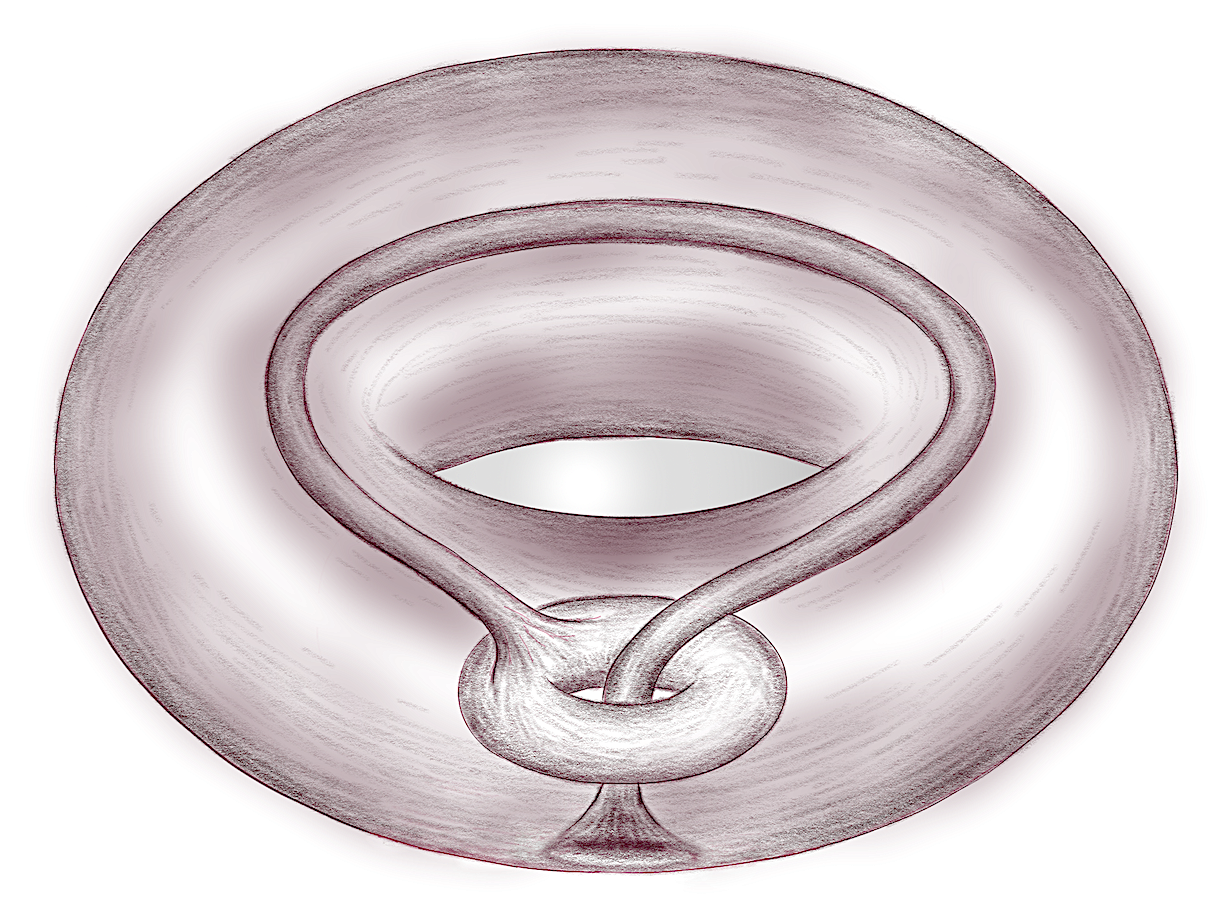
A kibogozáshoz elegendő lenne, ha a kisebb tóruszt a csövön keresztül tudnánk húzni. Ez három dimenzióban önátmetszés nélkül nem lehetséges, de négy dimenzióban már meg lehet csinálni. A négy dimenziót elegendő úgy elképzelnünk, mint a mi háromdimenziós terünkhöz hasonló háromdimenziós terek sokasága, amik párhuzamos hiperrétegekben helyezkednek el ahhoz a térhez képest, amiben a boroskancsó eredetileg van. Ez csak annyit jelent, hogy van egy a tér minden irányára merőleges negyedik irány, amely mentén kicsit odébbmenve (lefelé vagy felfelé) egy közeli háromdimenziós térbe jutunk, amely nem metszi az előzőt.

Vehetjük tehát a kis tóruszt, és minden pontjának elkezdjük megnövelni kicsit a negyedik koordinátáját, azaz eltoljuk egy párhuzamos rétegben lévő térbe, ott elmozdítjuk, és összehúzzuk annyira a tóruszt, hogy az eredeti térbe való visszatolás után már a csövön kívül kerüljön, vagyis lényegében kikerüljük a csövet. Eközben a kis tóruszból kiinduló cső helye maradhat változatlan. Miután a belső tórusz már nem hurkolódik rá a csőre, a háromdimenziós téren belül is ki tudjuk már gubancolni a tórusz belsejébe forduló tóruszt.

Füles tórusz!

Amilyen állapotban most vagyunk, az lényegében egy tórusz, aminek a belsejében van egy kisebb tórusz, ami egy befele türemkető köldökzsínóron lóg a nagy tórusz belsejében. A zsinórt azonban most már a nagy tórusz lyuka körül vissza tudjuk húzni, egészen lerövidítve a két tóruszt összekötő csövet. Sőt a cső teljesen összehúzható, és lényegében két tóruszunk marad, amik egy körlap mentén összenőttek, mégpedig úgy, hogy a kisebb a nagy belsejébe türemkedik. Ez azonban nem más, mint egy füles tórusz, aminek a fogója nem kifele lett ráragasztva, hanem befele türemkedik. Ez a befele türemkedő fül azonban nem más, mint egy görbe lyuk a tórusz felületének egy részén. A lyuk alakja azonban lényegtelen, a görbületet ki is egyenesíthetjük, a lyukat odébb is tolhatjuk, tehát a kapott felület valóban a kétlyukú tórusz lesz.

A négy dimenzióban való kigubancolásra egyébként csak egy megoldást kaptam, mégpedig egy igazi topológustól, aki a topológiát profi módon népszerűsíteni is szokta. Csak ajánlani tudom Pintér Gergőnek a lyukakról szoló előadását Youtube-on, vagy a TEDx előadását, amiben ugyancsak előkerül a Klein-kancsó, de úgy általában is ajánlom a MateMorfózis előadássorozatot, amin jó magam is előadtam még a régi Gólyában. Sőt a kint és a bent fogalmáról, amit most körbejártunk kicsit, Gergő még dalszöveget is írt, amit zenekarával a (halál;orgazmus) előadnak.