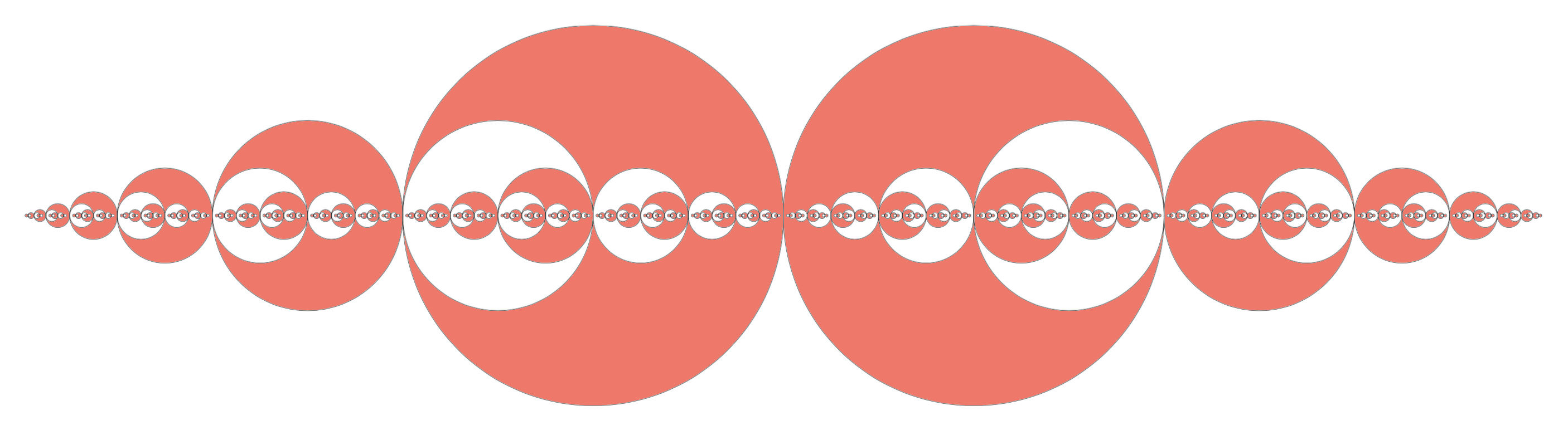
A fraktálok felettébb  érdekes objektumok. Egyfelől úgy tűnhet, hogy csupán érdekes matematikai konstrukciók, mint például a 43. feladványban megkonstruált fraktál, amit az alábbi ábra is mutat, és aminek a területe és a kerülete volt a kérdés; másfelől fraktálok vesznek körbe minket mindenhol, kiváltképp a természetben. Fraktál a fák gyökérzete és lombkoronája, a levelek erezete, a felhők, a villámok, a hópihék és a zúzmara, és még nagyon hosszan sorolhatnánk a példákat. Ezek a természetben előforduló fraktálok gyönyörködtetik a szemünket, és szebbnek találjuk őket, mint az egyszerű és rideg geometriai formákat.

A fráktálok már olyannyira részévé váltak a közbeszédnek, hogy szinte mindenki felismeri és érteni véli a fraktálok mibenlétét. Ehhez nyilván hozzájárul az is, hogy a fraktáloknak általában van két matematikai definíciók nélkül is könnyen felismerhető tulajdonságuk. Az egyik a látszólagos bonyolultságuk, ami többnyire abban nyilvánul meg, hogy az egyszerű geometriai objektumokkal ellentétben végtelenül részletgazdagok, sokszor végtelenül rücskösek vagy lyukacsosak. Másrészt az önhasonlóság jeleit mutatják, azaz felnagyítva egy kis részüket, ugyanazt a struktúrát fedezhetjük fel bennük, mint amit nagyobb skálán az egész alakzat mutat.

Mindkét tulajdonságot jól szemlélteti a fenti fraktál, hiszen az önhasonlóságot a konstrukció maga generálja. Ha csak a fraktál egyik felét, mondjuk a jobb oldali részt tekintjük, akkor annak felére kicsinyített mását megtaláljuk az eredetiben. Sőt, a felére kicsinyített más még a fraktál inverzében is egzaktul megtalálható, vagyis a kimaradó fehér rész is pontosan ugyanolyan struktúrát mutat, mint a beszínezett rész. Éppen ez a megállapítás az, aminek felismerése a feladvány megoldásában is nagy segítség, hiszen a fraktál területe két nagy kör területével lesz azonos. Ezt szemlélteti az alábbi ábra, ahol a fraktál két farkát visszatükröztük, és így a nagy körökbe visszafordítva éppen kitöltik azokat. 

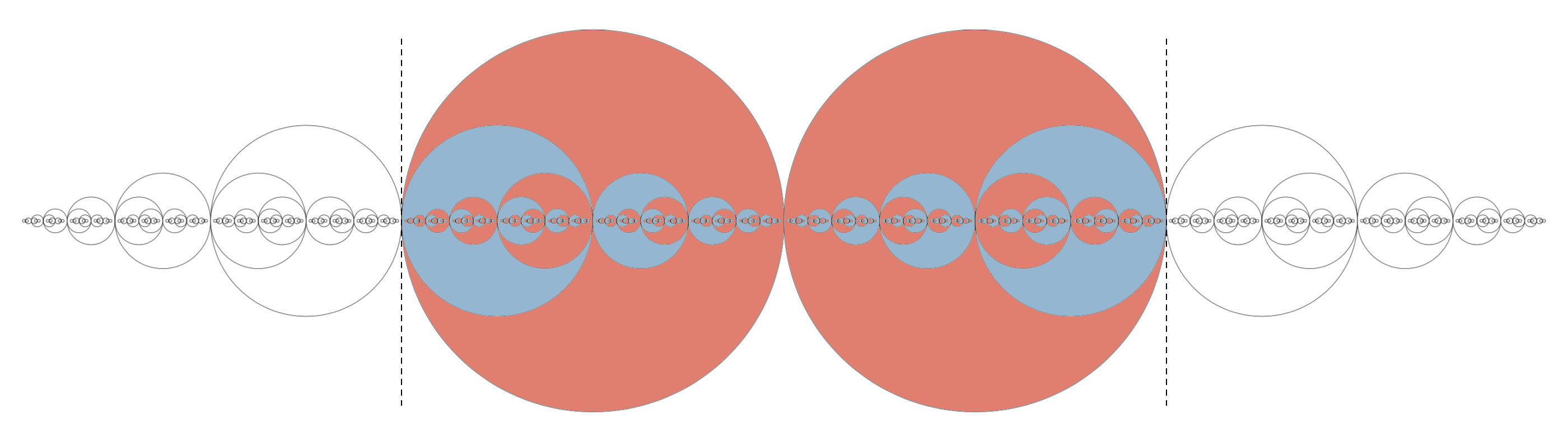
Ezzel a területre vonatkozó kérdést megválaszoltuk, nézzük hát a kerületet. A kerülethez a lerajzolt körök kerületének összhosszát kell kiszámolnunk, hiszen a felváltva színezés miatt minden körív határolja valahol a fraktál korallpirosra színezett területét. 

Vegyük rendre az azonos nagyságú köröket! Nagy körből kettő van, feleakkorából négy, negyedakkorából nyolc, és így tovább. A feleakkora kör kerülete feleakkora, a negyedakkoráé negyedakkora, mint a legnagyobb kör kerülete, és így tovább. Mivel a feleakkora körök kerülete egyenként fele annyi, de kétszer annyi van belőlük, így összességében a feleakkora körök kerületeinek összege ugyanannyi, mint a két nagy kör kerülete. És ez a fraktálban szereplő bármekkora méretű egyforma körökre igaz, mivel viszont végtelen sok méret szerepel, ezért végtelen sokszor kell vennünk a két nagy kör kerületét, vagyis összességében végtelen a fraktál kerülete.

Ha valakinek zéró a súlya, lehet szüksége végtelen nagy ruhára?

Azt kaptuk tehát, hogy ez a fraktál, ahogy nagyon sok matematikai fraktál, furcsa tulajdonságokat mutat. Véges a területe, de végtelen a kerülete. Hasonló módon az is lehetséges térben, hogy egy absztrakt matematikai objektumnak véges a térfogata, de végtelen a felülete. Gondoljunk csak arra, hogy a feladványban szereplő konstrukciót körök helyett gömbökkel is végigjátszhatjuk. Nem véletlen, hogy például a tüdőnk is fraktálszerkezetű, hiszen az evolúció során arra törekedett ez a szerv, hogy minél nagyobb legyen a felülete, és ezt egy méretskálákon keresztülívelő hasonló struktúra szerint felépülő, majdnem végtelenül rücskös és elágazó felülettel tudta könnyen elérni.

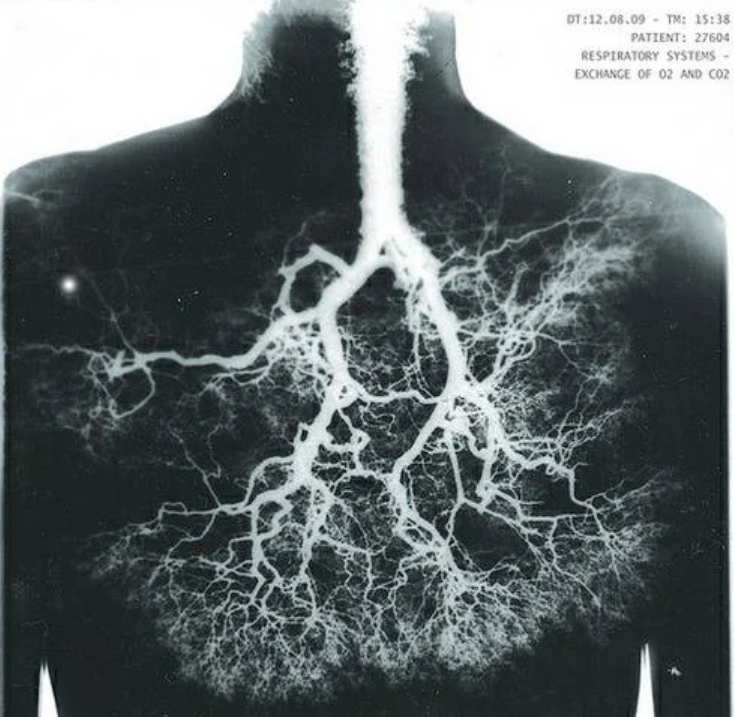
De van még ennél nagyobb furcsaság is, az absztrakt matematikai fraktálok körében. Végtelen kerületet ugyanis nem csak véges területű objektum tud produkálni, de még zérus területű is. Erre egy nagyon szép példa az úgynevezett Sierpinski-szőnyeg, vagy térben a Menger-szivacs, aminek végtelen a felülete miközben zérus a térfogata.

A Menger-szivacsot például úgy kapjuk, hogy kiindulunk egy kockából, azt 3×3×3 részre osztjuk, és kivesszük a középső hét kis kockákból álló keresztet, ahogy az alábbi ábrán is látható az első lépés után. Aztán minden további lépésben felosztjuk a maradék kockákat, és kivesszük mindegyiknek a közepét. Ha ezt a végtelenségig folytatjuk, könnyen belátható, hogy a maradék térfogata zérushoz tart, hiszen egy lépésben a kockáknak mindig eltávolítjuk fixen az 7/27 részét, azaz körülbelül a 26 százalékát. 15 lépés múlva például már csak (20/27)^15 része marad az eredeti kockának, ami nagyjából 1 százalékot tesz ki.

A Menger-szivacs tehát egy olyan végtelenül lyukacsos szivacs, aminek nincs térfogata, de végtelen sok pont marad benne, sőt a végtelen sok eltávolított lyukat végtelen nagy felület határolja, a felület ugyanis százalékos arányban mindig csak nő. Hogy pontosan mennyivel nő a felület lépésenként, azt a kedves olvasóra bízom.

De mi is az a fraktáldimenzió?

A fraktálok végtelenül részletgazdagok, másképp úgy is fogalmazhatunk, hogy különböző felbontással mindig új és új részletek tárulnak fel, amik struktúrája persze hasonló, de a kerület vagy a terület a felbontással általában változik, ahogy azt láttuk a példákon is. A változó terület akár zérushoz is tarthat, a fraktálban mégis maradnak pontok, amik az adott fraktálra jellemző struktúrát mutatnak. A fentiek alapján tehát jó megközelítésnek tűnik, hogy a fraktálok jellemzéséhez megvizsgáljuk azt, hogyan változik például a területük, vagy magasabb beágyazási dimenzióban a térfogatuk, attól függően, hogy mekkora felbontással tekintünk rájuk.

Egy hagyományos geometriai idom esetében ez a változás a dimenzóval áll összefüggésben. Ha veszünk például egy négyzetet, akkor feleakkora négyzetekből négy darab kell a lefedéséhez, és általában k-ad akkora oldalhosszú négyzetekből k^2-re lesz szükség a lefedéséhez. A 2-es szám a kitevőben pont a négyzet dimenzióját mutatja. Önhasonló alakzatokra általában is meghatározható ez a kitevő: ha N darab k-ad részére kicsinyített másra van szükség az eredeti lefedéséhez, akkor az úgynevezett önhasonlósági dimenzió D = log(N)/log(k). Kocka esetén k-ad akkora kis kockából N = k^3 darab szükséges, hogy kirakjuk az eredeti kockát, tehát a kocka dimenziója D = log(k^3)/log(k) = 3·log(k)/log(k) = 3, ahogy azt várjuk.

Nem egész dimenzió? Az meg mit jelent?

De nemcsak a négyzet és a kocka önhasonló, hanem nagyon sok fraktál is egzaktul önhasonló. A fentebb bemutatott Menger-szivacs is ilyen, amit az eredeti harmadára kicsinyített másaiból, szám szerint húsz darabból tudunk kirakni, tehát a hasonlósági dimenziója D = log(20)/log(3) ≈ 2.73. A Menger-szivacs anyagának a dimenziója tehát 3-nál kisebb, ugyanakkor a felületének a dimenzióját is ki lehet számolni, amire biztatok minden kedves olvasót, és erre egy 2-nél nagyobb szám adódik majd. A Menger-szivacs tehát egyfajta átmenetnek tekinthető a kétdimenziós felület és a háromdimenziós kocka között.

A természetben előforduló fraktáloknál azonban ez az önhasonlóság többnyire nem egzakt, hanem csak statisztikai jellegű. Egy fa kisebb ága nagyon hasonlóan néz ki, mint egy nagyobb ág, de sosem a pontos kicsinyített mása. Ezért is nehéz matematikai precizitással megfogalmazni az önhasonlóságot, és úgy általában definiálni, hogy mik a fraktálok. Talán meglepő, de erről nincs is megállapodás a szakirodalomban, maga Benoît Mandelbrot lengyel származású francia-amerikai matematikus, a fraktál elnevezés atyja is elvetett minden definíciót, amivel próbálkoztak.

De mit lehet csinálni a fraktál dimenziójának kiszámítása ügyében, ha egy fraktál nem egzaktul önhasonló? A módszer továbbra is ugyanaz, hogy a felbontás függvényében nézzük a terület vagy a térfogat változását. A lefedéshez használt egységeknek azonban nem kell az eredeti alakzattal hasonlóknak lenniük, használhatunk standard négyzeteket vagy kockákat is mérőegységnek. Ha egy adott k-felbontásnál a mérőegységünk 1/k oldalú négyzet vagy kocka, és ezekből minimálisan N(k) darabra van szükség, hogy lefedjük velük a teljes fraktált, akkor ezen a felbontáson a dimenzió becslését a D(k) = log(N(k))/log(k) kifejezés adja. Ha finomítjuk a felbontást, azaz k-val tartunk a végtelenbe és D(k) eközben egy konkrét értékhez tart (konvergál), akkor ezt a határértékét nevezzük a fraktál úgynevezett dobozdimenziójának vagy dobozszámlálási dimenziójának, amire még Minkowski–Bouligand-dimenzió néven is szokás hivatkozni.

A dobozdimenzió természetesen önhasonló alakzatokra visszaadja a korábbi hasonlósági dimenziót, akkor ugyanis D(k) egzaktul ugyanazt az értéket adja sok különböző felbontásra. Nem egzaktul önhasonló fraktálok esetén, továbbá  sztochasztikus fraktálok esetén, amiket véletlen folyamatok határoznak meg, nem várhatjuk el, hogy D(k) minden k-ra ugyanazt adja, ezért D(k) picit fluktuálhat, de nagy felbontásra tipikusan konvergál egy konkrét értékhez.

A gyakorlatban persze valódi alakzatok vagy a természetben előforduló fraktálok esetében nem lehet a végtelenségig folytatni a felbontás növelését, mert általában fizikai korlátokba ütközünk, például a térfogatszámításban nem mehetünk le a molekulák szintjére. Ugyanakkor, ha D(k) több nagyságrenden keresztül viszonylag állandó, akkor fraktálról szokás beszélni, és a fraktáldimenziót ezen a tartományon mérni és becsülni lehet. 

Nagy-Britannia vagy Norvégia partvonalát szokták erre példaként felhozni, amelyek partvonalait különböző hosszúságú „vonalzókkal" lemérhetjük. Lehet az egységünk mondjuk 100, 10 vagy 1 kilométer, de mondjuk a kavicsok nagyságrendjében már értelemtlenné válik a partvonal hossza. A mérések alapján mindenesetre több nagyságrenden keresztül érvényes, hogy log(N(k))/log(k) körülbelül konstans, amiből Nagy-Britannia partvonalának fraktáldimenziójára D ≈ 1.25, Norvégiára partvonalára pedig D ≈ 1.52 adódik. Ami pedig a korábban említett emberi tüdőt illeti, most már eljutottunk oda, hogy megértsük, mit is jelent, ha azt mondjuk, hogy a fraktáldimenziója 2.93. Megállapíthatjuk, hogy az evolúció elég jó munkát végzett.

Bandzsítós fraktál haladóknak

Láthatjuk, hogy a legtöbb fraktál dimenziója nem egész szám. Ennek alapján gondolhatnánk azt, hogy fraktál az, aminek a dimenziója nem egész. Mármost a 43. feladványban szereplő fraktállal éppen azt szerettem volna demonstrálni, hogy ez a próbálkozás sajnos nem működőképes. Több megoldónk is ki tudta számolni, hogy a bandzsítós fraktál területének dobozdimenziója 2, a kerületének dobozdimenziója pedig 1, tehát sem a fraktál belseje, sem annak kerülete nem lenne fraktál, ha elfogadnánk a fenti definíciót, márpedig a bandzsítós fraktál fraktál mivoltát valósznűleg senki nem kérdőjelezi meg.

Ami a bandzsítós fraktál dobozdimenziójának számítását illeti, ahhoz csak vázlatosan adnék rövid útmutatót. A terület dobozdimenziója nagyon egyszerű, mert a fraktál nem minden részén végtelenül lyukacsos, azaz van olyan része, ahol tartalmaz egy akármekkora kicsi négyzetet, és mivel annak dimenziója 2, ezért az az egész fraktált dominálni fogja. Hiába lenne ugyanis kisebb a négyzeten kívüli rész fraktáldimenziója 2-nél, N(k)-ban minig a 2-dimenziós részből származó tagok dominálnának. Láthatjuk tehát, hogy a dobozdimenzió olyan fraktálok jellemzésére nem alkalmas, amik tartalmaznak nem fraktális részeket is. Márpedig szeretnénk azt gondolni, hogy egy fraktál attól függetlenül fraktál, hogy mi van még hozzácsapva mellékesen.

A kerület dobozdimenziójának számolásához érdemes olyan rácsot használni, amely alapegysége a nagy kör köré írt négyzet, és amelynek oldalai párhuzamosak a fraktál szimmetriatengelyeivel. A négyzetrács felbontását felezéssel érdemes növelni, és észre kell venni, hogy adott felbontás esetén egy bizonyos méret alatti körök lefedésével már nem kell fogalkoznunk. A nagyobb körvonalak lefedéséből pedig érdemes egy alsó és egy felső korlátot kikalkulálni N(k)-ra, mert kiderül, hogy bármelyikkel is számolunk log(N(k))/log(k) ugyanoda konvergál, tehát nem szükséges egzaktul kiszámolni N(k)-t.