Bűvös négyzetnek az olyan számtáblázatot szokták nevezni, amiben minden sorban és minden oszlopban ugyanannyi a számok összege, sőt még az átlókban is. A bűvös gyufanégyzet feladványban négy gyufaszálat volt szabad áthelyezni, hogy kapjunk egy bűvös négyzetet gyufákból kirakott digitális számokkal.

A megoldáshoz a jobb alsó nyolcasból el kellett venni a három vízszintes gyufaszálat, így lett a 8-ból 11, és a 89-ből kellett elvenni még egy gyufaszálat úgy, hogy 85 maradjon. Az elvett gyufákból kettőt arra használunk, hogy a 2-es elé teszünk egy 1-es számjegyen, így lesz abban a rublikában 12, egyet-egyet pedig arra használunk, hogy a 10-ből és 20-ból rendre 18 és 28 legyen. Így egy olyan bűvös négyzetet kapunk, amelyben a sorok és oszlopok, sőt az átlók összege is 176. De ez nem minden. A sarkokban lévő négy szám és a középső négy szám összege is 176. Sőt ha vesszük a szemközti oldalak középső két-két számát, akkor ezek összege is mindig 176, például 18+51+85+22 = 176.

Hogy miért tud ilyen sokat ez a bűvös négyzet, arra szépen rávilágít, ha megnézzük, hogy milyen mintázatuk van a számoknak. Vegyük észre, hogy vannak tízes, húszas, ötvenes és nyolcvanas számok a táblázatban, mindegyikből 4-4 darab. Az egy csoporton belüli számok mintázatát érdemes megfigyelni: egy sorban, egy oszlopban, egy átlóban sosincs két szám ugyanabból a csoportból. Tehát például nem fogunk két nyolcvanas számot találni egy sorban vagy oszlopban. Ez azt eredményezi, hogyha az egy csoporton belüli számoknak, páldául az összes nyolcvanas számnak az értékét x-szel növelem, vagy csökkentem, akkor a teljes négyzet bűvös tulajdonsága továbbra is megmarad, csak x-szel változik a sorok és oszlopok összege. Tehát a mintázatok alapján bárki tud hasonló bűvös négyzeteket kreálni.

De ez a bűvös négyzet speciális, van ugyanis még egy érdekes tulajdonsága. Többen is észrevették, hogy csak bizonyos digitális számjegyek szerepelnek ebben a bővös négyzetben, de azt már kevesebben, hogy miben speciálisak ezek a számjegyek: abban, hogy fejjel lefelé is értelmes számjegy mindegyik. Ha pedig az egész bűvös négyzetet fejjel lefelé fordítjuk, akkor is bűvös négyzetet kapunk, ráadásul ennek is 176 az összegszáma.

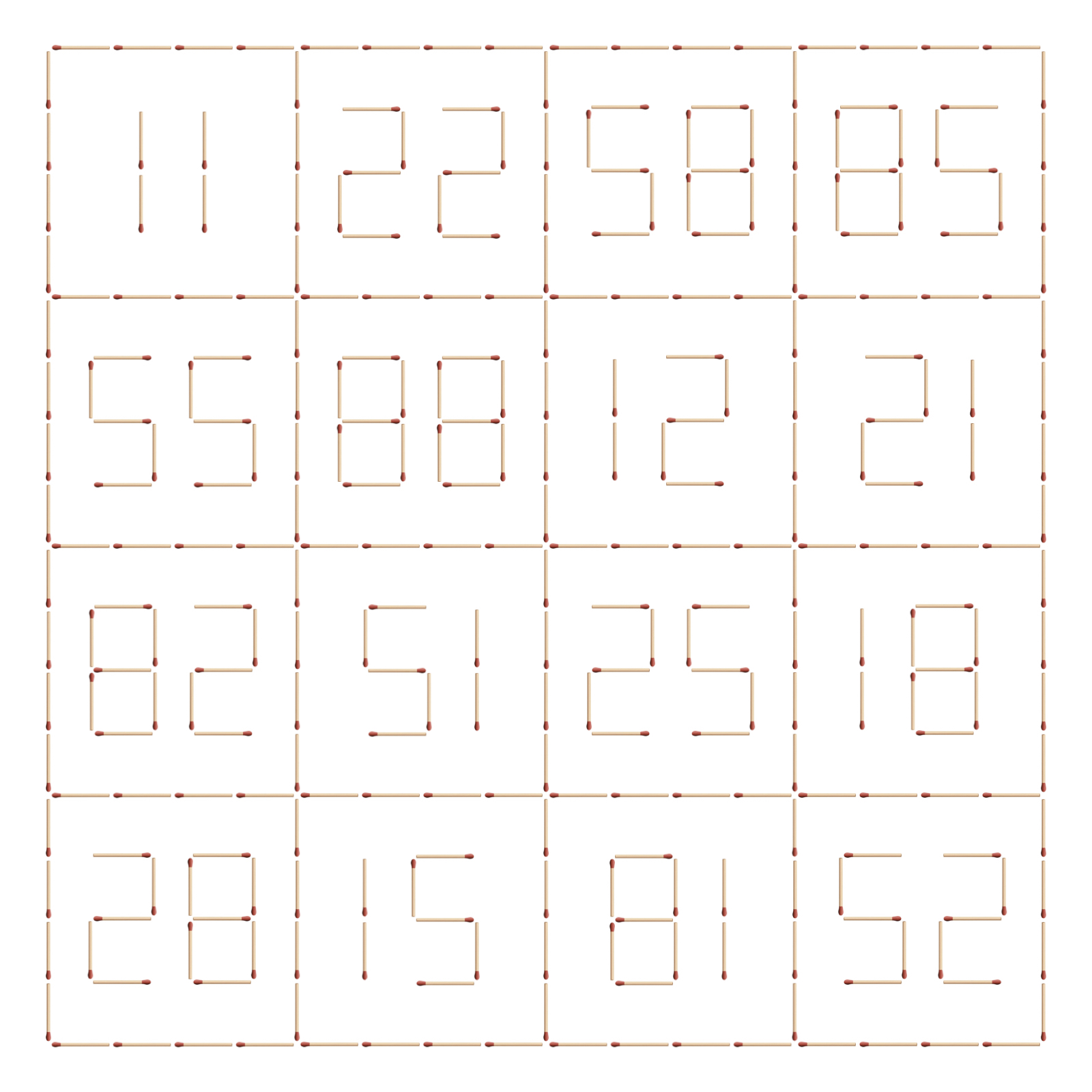
De a négyzet még ennél is különlegesebb: ha egy tükörben nézed, még akkor is értelmes, sőt így is bűvös négyzet, és ennek is 176 az összegszáma.