A cím alapján azt hihetitek, hogy az ismert viccet fogom elmesélni, hát elmesélem, aztán jön majd az Ész Ventura-feladat megoldása is.

Egy szállodában tűz üt ki éjszaka, és a füstszagra felébred a szinten lakó matematikus is. Kirohan a szobából, meglátja a folyosó végén a tüzet, és tőle pár méterre a poroltó készüléket.
– Ah! Létezik megoldás – nyugtázza, és elégedetten visszafekszik aludni. 

Más változatban:

– Ah! A megoldás innen már triviális – állapítja meg, és nyugodtan visszafekszik aludni.

A brazil erdőtüzek kapcsán kitűzött feladványunkban azonban a következő volt a kérdés. Ha tudjuk, hogy egy 30 km sugarú körön belül 241 pontszerűnek tekinthető tűz lángol, és egyszerre két 10 km sugarú körön belül elolthatunk minden tüzet, akkor meg tudjuk-e úgy választani a két tűzoltási területet, hogy biztosan el tudjunk oltani 30-nál is több tüzet?

A feladatot többféleképpen is meg lehet oldani. Az első megoldás során a skatulyaelv általánosított és folytonos változatát fogjuk használni. A skatulyaelv eredeti, Peter Gustav Lejeune Dirichlet 19. századi német matematikus által megfogalmazott diszkrét változata azt mondja ki, ha van n elemünk, és azokat m skatulyába helyezzük, akkor n > m esetén biztosan lesz olyan skatulya, amibe legalább két elem kerül. Roppant egyszerűsége ellenére ez az elv nagyon sokszor praktikusan alkalmazható a matematikában. Könnyen megválaszolható segítségével például az a nagyon sokakat foglalkoztató kérdés, hogy van-e Budapesten két olyan ember, akiknek ugyanannyi szál hajuk van. A válasz igen, hiszen egy ember hajszálainak száma általában 100 000 és 200 000 közötti, de semmi esetre sem több a milliónál, Budapesten viszont többen laknak egymilliónál.

Hogyan néz ki a skatulyaelv folytonos változata, és hogyan fogjuk alkalmazni ebben a feladványban? Rajzoljunk a 241 gócpont (az ábrán piros pontok) mindegyike köré egy 10 km sugarú kört (szaggatott körök). A továbbiakban ezeket hívjuk kis köröknek, de az illusztráción nem rajzoltuk be mind a 241-et. Ezek a körök biztosan benne vannak egy 40 km sugarú körben, továbbiakban nagy kör (legkülső), hiszen a 30 km sugarú körtől (sötétszürke terület) 10 km-nél távolabb nem lóghatnak ki.

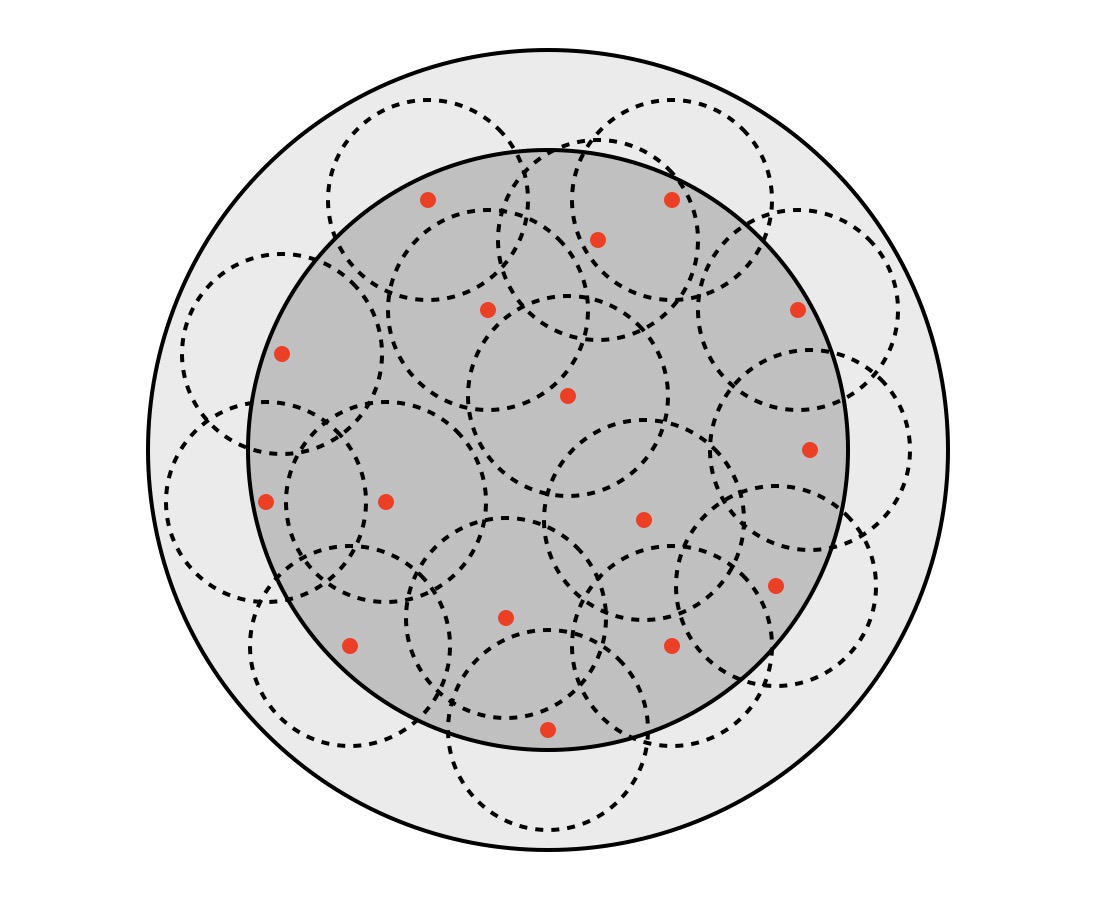
A 241 darab 10 km sugarú kör együttes területe legyen 241·T, ahol T egy kis kör területe. Mármost a nagy kör területe 16·T, aminél a kis körök összterülete sokkal több, ezért a kis köröket nem tudjuk átfedésmentesen bezsúfolni a nagy körbe, vagyis biztosan lesz olyan pont, ami legalább két kis körbe is beleesik. Sőt, ha a nagy kör területét 15-ször vesszük (15 × 16 = 240), még akkor is kisebb területet kapunk, mint a kis körök összterülete. Ennek az a következménye, hogy mindenképpen lesz olyan pont a nagy körben, ami benne lesz több mint 15 kis körben, tehát legalább 16 kis körnek is belső pontja lesz. Ezt mondja ki az általánosított és folytonos skatulyaelv.

Mármost vegyünk egy ilyen pontot, ami 16 kis kör közös metszetébe esik. Erre a pontra teljesül, hogy 10 km-nél közelebb van hozzá mind a 16 kis körnek a középpontja, azaz 16 gócpont. Válasszuk ezt a pontot az egyik tűzoltási terület középpontjának, így 16 tüzet már biztosan el tudunk oltani. Kérdés, hogy még 15-öt el tudunk-e oltani egy megfelelően választott másik tűzoltási területtel. A válasz igen, és nagyon hasonlóan fogunk eljárni, mint eddig.

Ha az eredeti sötétszürke tartományból kivesszük azt a 16 gócpontot, amit sikerült eloltanunk, akkor marad még 241-16 = 225 gócpont a sötétszürke területben, és az a kérdés, hogy tudunk-e választani még egy olyan tűzoltási területet, amibe 15 beleesik ezekből.

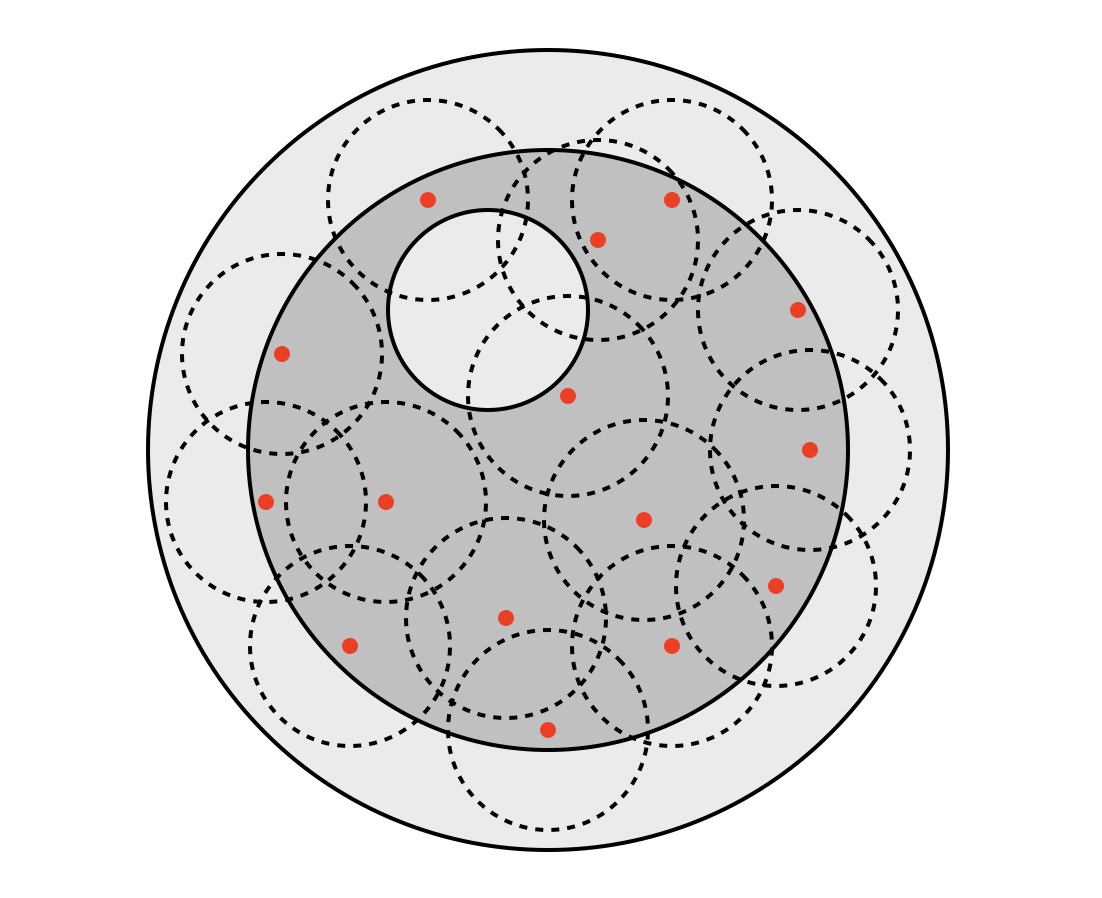
Ehhez megint rajzoljunk minden maradék gócpont köré egy 10 km sugarú kört, ahogy korábban, lásd a szaggatott köröket a második ábrán. Ezek a körök továbbra is beleesnek a nagy 40 km sugarú körbe. A 225 gócpont köré írt kis körök összterülete 225·T, ami a 16·T területű nagy kör 14-szeresénél nagyobb (14 × 16 = 224 < 225), tehát lesz olyan pont, ami legalább 15 kis körnek is része, és egy ilyen pontot választva a második tűzoltási terület közepének, 15 tűz eloltható, vagyis összesen 16+15 = 31, amit szerettünk volna.

Lehet többet?

Lehet azonban ennél még többet is. A skatulyaelv csak a területet vette számításba, de ha körökkel akarunk lefedni egy területet, akkor nemcsak a terület számít, hanem a geometria is. A körökkel való fedés a matematika ismert problémája; általános megoldás nincs ugyan rá, de az eddig talált optimális fedéseket számon tartják, megtalálhatók például itt. Mármost a fenti forrás alapján 14 darab 10 km sugarú körrel teljesen le lehet fedni egy 30.14 km sugarú kört. Ez alapján belátható, hogy a tűzoltók legalább 36 tüzet el tudnak oltani. Boros Péter olvasónk gondolatmenete erre az alábbi:

Vegyük a fedésben résztvevő 14 kör közül azt, amely belsejében a legtöbb tűz van. Legyen az ebben levő tüzek száma n. Ekkor n legalább 18, hiszen ellenkező esetben minden körben legfeljebb 17 tűz lenne található, azaz összesen legfeljebb 14 × 17 = 239, ami kevesebb, mint 241. Ha a második legnépesebb körbe is legalább 18 esik, akkor az első kettőbe legalább 36, vagyis rendben vagyunk. Ha a másodikba csak 17, akkor viszont az elsőbe legalább 241 - 13×17 = 20 és így a az első kettőbe legalább 37. Ha a másodikba 16, az elsőbe legalább 241 - 13×16 = 33, együtt pedig legalább 49. Végül pedig, ha a másodikban 15 vagy kevesebb van, akkor az elsőben egyedül legalább 241 - 13×15 = 46 található.