Ész Ventura: Emlékezzünk a játszóterekre!
Játszóteres feladványunk a járvány alatt nem annyira aktuális, mint amikor megjelent tavaly szeptemberben, de ha vége lesz a kijárási korlátozásoknak, a szülők már felkészültebben vihetik játszótérre a csemetéiket, ha tekintetbe veszik a játszótér beláthatóságáról szóló eredményeinket. Az volt a kérdés, hogy hova érdemes elhelyezkednie az anyukának, ha a négyzet alakú játszótér legnagyobb részét szeretné belátni. A pirossal jelölt kör alakú játszóváron nem lehet keresztüllátni.
Tudjuk, hogy a játszóvárat pont érintik a sarkokból a négyzet oldalainak felezőpontjaiba menő ösvények (szaggatott vonalak). Legyen a négyzet oldala két egység. Kihasználva azt, hogy az érintő egyenesek merőlegesek az érintési pontba húzott sugárra, néhány Pitagorasz-tétel felhasználásával hamar kikalkulálhatjuk a kör sugarának értékét, ami r = 1/√5 lesz.
Vegyük észre, hogy minél messzebb van egy pont a körtől, annál nagyobb annak a köríves háromszögnek a területe, amit a körhöz húzott érintők és a két érintési pont között futó rövidebb körív határol. Ezt felhasználva beláthatjuk, hogy az anyuka számára optimális pont biztosan a négyzet kerületén lesz valahol. Ha ugyanis veszünk egy P' belső pontot, akkor a kör középpontjából a P' pontba menő szakaszt meghosszabítva a négyzet kerületéig, a kerületen kimetszett P pont biztosan jobb lesz P'-nél, ez könnyen belátható.
Mármost szimmetria-okokból a négyzet kerületén is elegendő az egyik saroktól egy szomszédos oldalfelező pontig vizsgálódni. Azt is tudjuk, hogy a két szélső pont közül a sarok a jobb, mert ott a köríves háromszög területe nagyobb, a maradék belátható terület pedig mindkét esetben a négyzet területének pont a fele az ösvények speciális elhelyezkedésének köszönhetően. Kérdés, hogy a sarokponttól közeledve a felezőpontig találunk-e jobb őrhelyet.
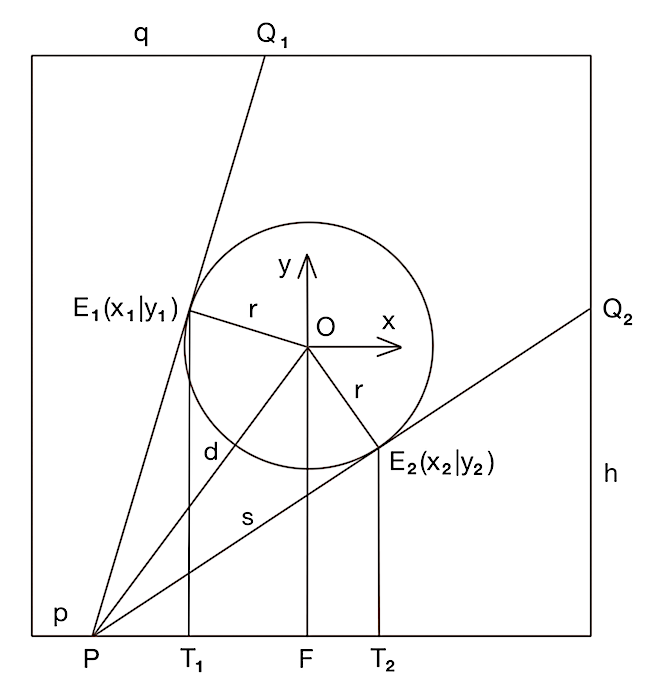
Legyen 0 ≤ p < 1 a négyzet kerületén lévő P pont távolsága a saroktól. Jelöljük E1-el és E2-vel a P pontból a körhöz húzott érintők érintési pontjait az ábra szerint. Helyezzük a koordinátarendszerünk origóját a négyzet középpontjába, és első lépésként számoljuk ki az E1 és E2 pontok (x1,y1) és (x2,y2) koordinátáit. A számoláshoz elhagyjuk az 1-es és 2-es indexeket, mert minden egyenlet, amit használni fogunk, egyszerre érvényes lesz mindkét érintkezési pontra.
Egyrészt az érintkezési pont a körön van, ezért a kör középpontjától vett távolsága r. Másrészt a POE háromszög derékszögű, amire felírhatunk egy Pitagorasz-tételt, hasonlóan a PFO háromszögre, ami ugyancsak derékszögű, mindkettőnek a PO az átfogója, aminek a hosszát jelöljük d-vel. A PE érintők hosszát jelöljük s-sel. Vegyük továbbá az E érintkezési pontok vetületeit a négyzet azon oldalára, amelyiken a P elhelyezkedik, legyenek ezek a T1 és T2 pontok. Ezek x-koordinátái megegyeznek rendre az E1 és E2 x-koordinátáival, azaz x1 és x2-vel. A PET derékszögű háromszög(ek)re is felírhatunk egy Pitagorasz-tételt. A kapott egyenletek az alábbiak lesznek:
x2 + y2 = r2
r2 + s2 = d2 = (1-p)2 + 1
(1-p+x)2 + (1+y)2 = s2
Küszöböljük ki s2-et az utolsó egyenletekből és x2 + y2 helyére helyettesítsünk be r2-et, így az alábbi egyszerűsítések után kapunk x és y között egy egyszerű elsőrendű összefüggést:
x2 + y2 + (1-p+x)2 + (1+y)2 = (1-p)2 + 1
x2 + y2 + (1-p)2 + 2·(1-p)·x + x2 + 1 + 2·y + y2 = (1-p)2 + 1
2·r2 + 2·(1-p)·x + 2·y = 0
y = (p-1)·x - r2
Ez az egyenlet az x2 + y2 = r2 egyenlettel együtt akár x-re akár y-ra megoldható, de mindkettőre másodfokú egyenlet adódik, vagyis két megoldás párt kapunk. Ezen nem csodálkozunk, hiszen két érintési pontunk van, így tehát mindkettő koordinátáit sikerül egyszerre megkapnunk. Ha valaki nem szeretne tovább számolni, az egyenletrendszer megoldásához kérheti például a WolframAlpha segítségét, csak ezt kell bepötyögni neki:
solve {1/5 = x^2 + y^2, y = (p-1)x - 1/5} for x, y
Illetve még ezt se, mert a fenti linkre kattintva már automatikusan ennek az egyenletrendszernek a megoldásához irányít, és itt már azt is figyelembe vettük, hogy r2 = 1/5. A megoldások így néznek ki:
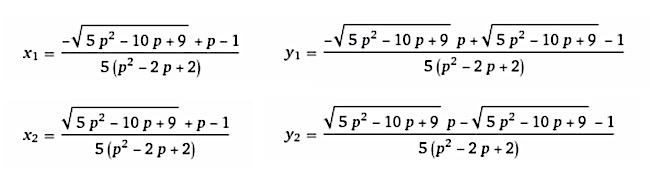
Ha megvannak az E1 és E2 érintési pontok fenti koordinátái, akkor az érintők meghosszabbítása által a négyzet túloldalán kimetszett Q1 és Q2 pontok koordinátáit is könnyű megkapni hasonlósági arányokat kihasználva. A Q1 pont y-koordinátája természetesen 1, csak az x-koordinátáját kell számolnunk, amit az ábrán q-val jelöltünk. A Q2 pontnak pedig az x-koordinátája 1, csak az y-koordinátáját kell számolnunk, amit az ábrán h-val jelöltünk. Abból a tényből fakadóan, hogy a P, Ei és Qi pontok adott i-re egy egyenesre esnek, az alábbi arányokat írhatjuk fel:
(q-p) : (1+x1-p) = 2 : (1+y1) ⇒ q = p+2·(1+x1-p)/(1+y1)
h : (1+y2) = (2-p) : (1+x2-p) ⇒ h = (1+y2)·(2-p)/(1+x2-p)
Mármost az anyuka által belátott terület összesen három részből tevődik össze: egy trapézból, egy háromszögből és egy körívvel határolt háromszegletből. A trapéz területe éppen p+q, a háromszög területe (2-p)·h/2, végül a körívvel határolt idom területe: s·r-arctg(s/r)·r2, ehhez a korábbi egyenletekből s-et ki kell fejeznünk. Például x1-et és y1-et visszahelyettesítve jelentős egyszerűsítések után az adódik, hogy
s2 = (1-p+x1)2 + (1+y1)2 = p2 - 2·p + 9/5.
Ezt felhasználva és a fenti három területet összesítve kirajzolhatjuk p függvényében, hogy miként alakul az anyuka által belátható terület. Az alábbi ábrán láthatjuk, hogy a belátható terület szigorúan monoton csökken a [0,1] intervallumon, maximuma a négyzet csúcsában, p=0 értéknél van.
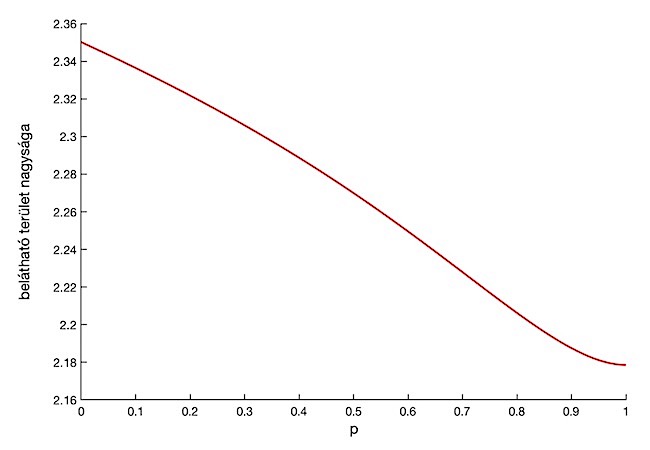
Haladóknak kérdés volt még, hogy milyen kicsi lehet a kör sugara, hogy a négyzet sarka még mindig a legjobb pont legyen. Ennél többet is mondhatunk: meg lehet mutatni, hogy r < ρ esetén az optimális megfigyelőpont egy oldal felezőpontja, míg r > ρ esetén valamelyik sarok, ahol ρ ≈ 0,345. Ne feledjük, hogy a négyzet oldalát 2 egységnek választottuk az elején.
Kérdés volt még az is, hogy általában hány anyuka szükséges a teljes terület megfigyeléséhez. Ha r > 0, akkor kettő biztosan nem elég, hiszen bármely körön kívüli pontból a körhöz húzott érintők érintési pontjai közötti rövidebb ív mindig kisebb mint egy félkörív, így két anyuka nem fedheti le a teljes kör kerületét. Másrészt négy anyuka a négy sarokba mindenképpen elég. Három anyuka pedig akkor elég, ha a kör sugara nem nagyobb, mint a legnagyobb, éppen a négyzetbe írt egyenlő szárú háromszögbe írt kör sugara, ahol a háromszög egyenlő szárai közötti csúcsa a négyzet egyik csúcsa. Ez r ≈ 0.561 sugárnak felel meg. A haladó kérdésre beküldött egyetlen megoldást köszönjük Boros Péter olvasónknak.
A szerző fizikus, bűvész. Az Ész Ventura korábbi feladványai és megoldásai itt olvashatók.
Kapcsolódó cikkek a Qubiten:
