Ész Ventura: Ajándék kockának nézd meg a színét!
88. feladvány: Négyszeres kockaburkolás
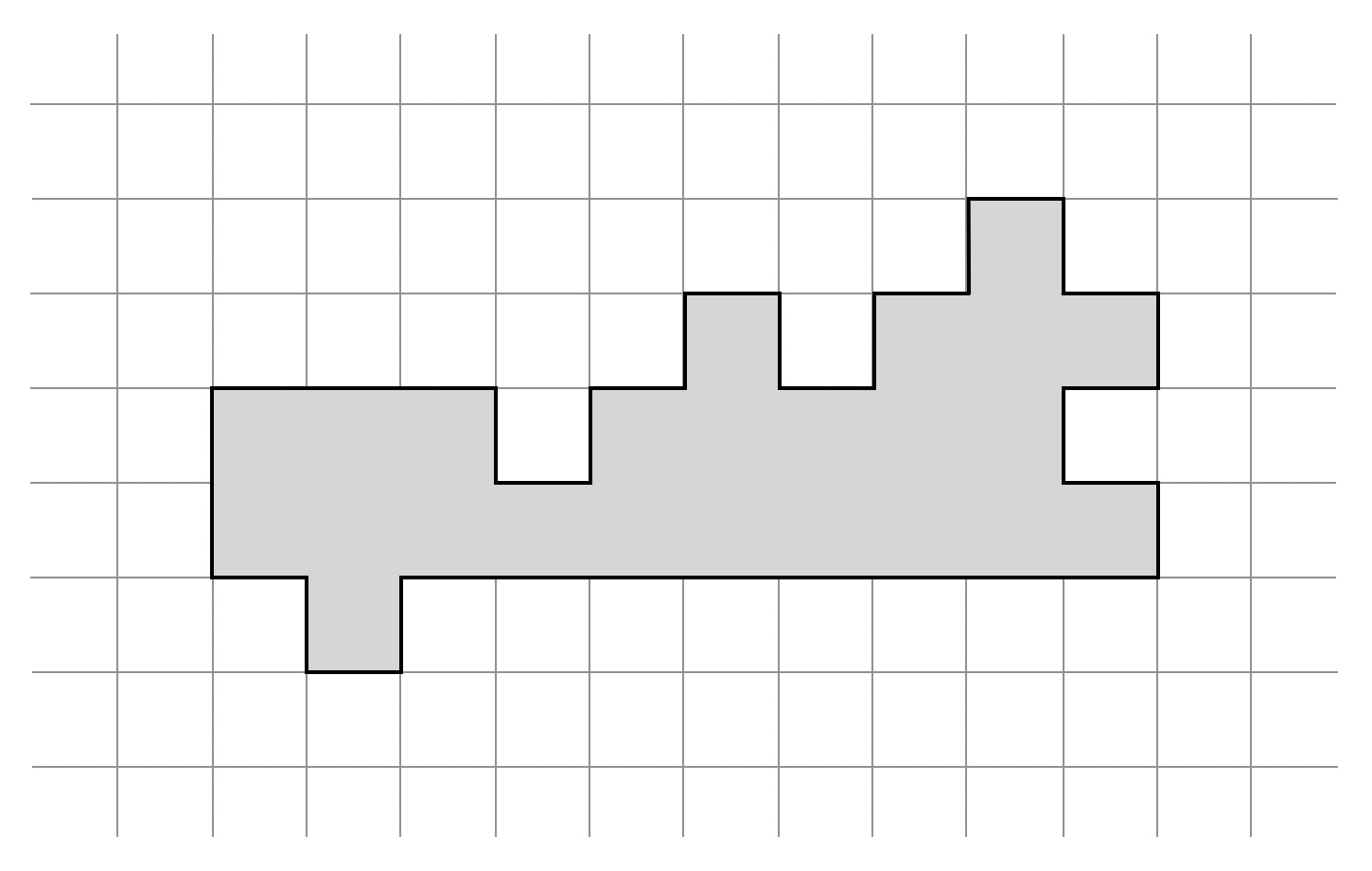
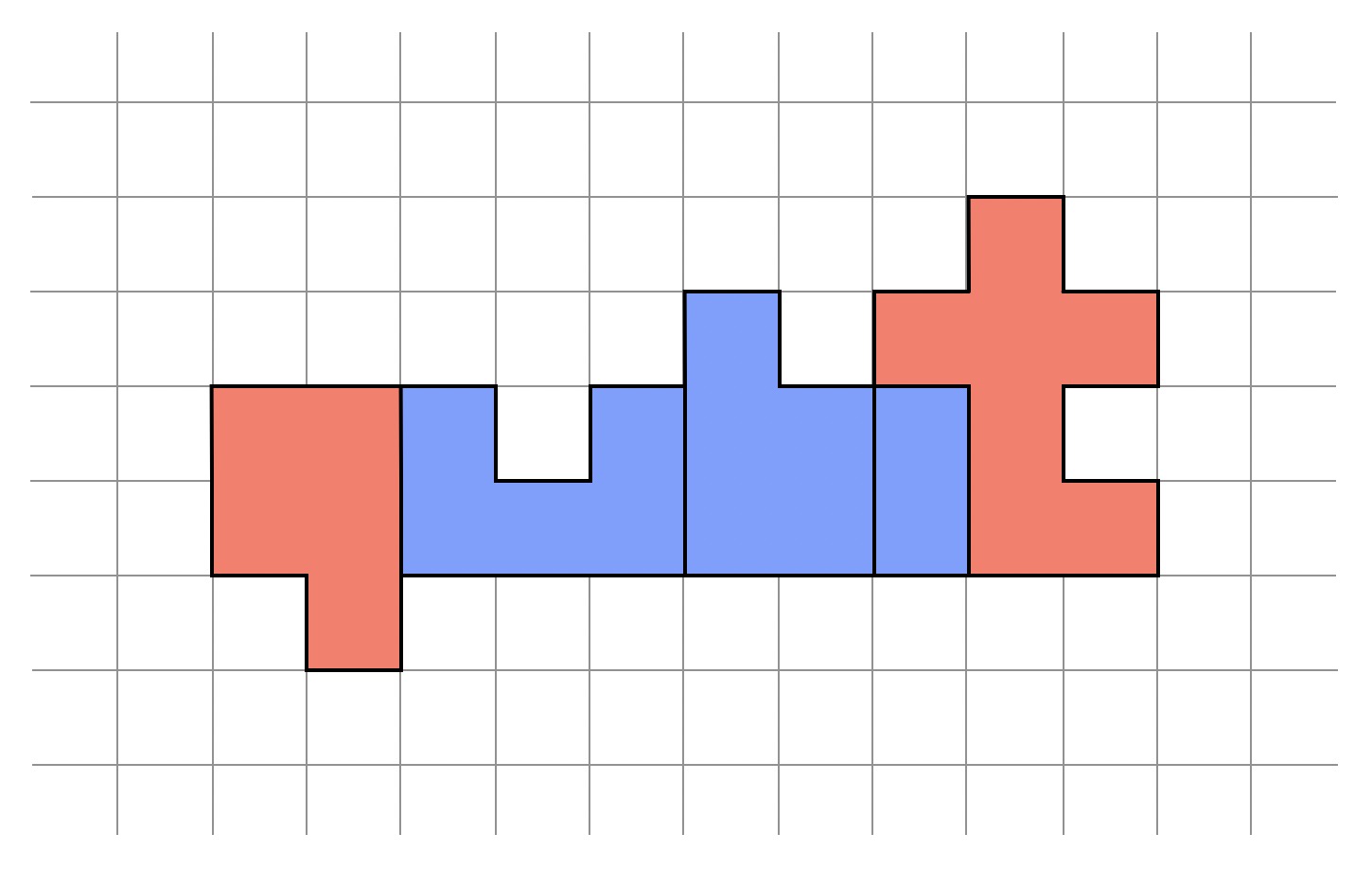
Vágjátok ki az 1. ábrán látható szürke tartományt egy négyzetrácsos papírlapból. Ezután színezzétek ki a tartományt a 2. ábrának megfelelően, vagyis qubit első és utolsó betűje legyen piros, a középső betűk pedig kékek. Fontos: a papír mindkét oldalát ki kell színezni, elöl is, hátul is.
A szürke tartomány éppen 24 egységnégyzetből áll össze, ami négyszer annyi, mint egy egységkocka felülete, tehát elvileg lehetőség van arra, hogy egy egységkockát négyszer, azaz négy rétegben beburkoljunk egy ekkora területű papírlappal. De meg lehet-e ezt úgy csinálni, hogy a papírdarab összefüggő maradjon? Megengedett, hogy vágásokat ejtsünk a papíron, de nem eshet szét darabokra.
További feltétel a feladathoz: a kocka minden oldalának pontosan négy rétegben kell beburkolva lennie, amiből a belső kettőnek kéknek kell lennie, a külső kettőnek pedig pirosnak. Menni fog?
Haladóknak bónusz kérdés: vegyünk egy ugyanilyen alakú papírt, ami az 1. ábrán látható, de most az egyik oldala legyen teljesen kék, a másik oldala pedig teljesen piros. Beburkolható-e ezzel úgy az egységkocka, hogy a kocka minden oldalát pontosan négy réteg fedje, de minden réteg belső oldala kék legyen, a kifelé forduló oldal pedig piros? Vágni továbbra is szabad, de nem eshet szét darabokra a papír. Ha nem lehetséges, tudod-e bizonyítani?
Nehézségi szint:
A megfejtéseket magyarázó ábrával és részletes magyarázattal vagy videóval együtt az eszventura@qubit.hu címre várjuk. A legértékesebb megoldást küldő versenyzők felkerülnek az Ész Ventura dicsőségfalára, közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: május 30. éjfél.
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus és bűvész.
Kapcsolódó cikkek a Qubiten: