Ételperfekcionizmus című fiktív utópisztikus feladványom tavaly novemberben az alábbi bevezetővel indult:

2042-re teljesen átalakul a gasztronómia. A szakácsok helyét átveszik az ételtervezők, legyenek azok emberek vagy szoftverek, a konyhákat pedig felváltják az ételnyomtatók. Tetszőleges étel elkészítése lehetséges lesz, a kérdés már csak az marad, hogy hogyan választunk. Egyesek a hobbi-ételtervezők munkáinak digitális receptúráját töltik majd le a netről, másoknak professzionális algoritmusok állítják elő ízlésüknek megfelelően személyre szabott étrendjüket. Az ételeket legtöbb esetben drónnal szállítják ki frissen és melegen az ételnyomtató cégek.

Az idei év legelején pedig egy Qubiten megjelent cikkben az alábbiakról adtunk hírt.

A technológiai újítások egész garmadáját igénylő posztmodern laboratóriumi farmgazdálkodás ma még drága mulatságnak tűnhet, de Monbiot szerint a tömegtermelés beindulásával az új iparág gyorsan gazdaságossá válik majd. Egy brit-amerikai thinktank, a RethinkX friss felmérése egyenesen azt állítja, hogy a molekuláris élelmiszeripar a technológiai fejlődésnek köszönhetően alig néhány tíz év múlva, már az évszázad közepére felváltja a hagyományos farmgazdálkodást. Az új modellben molekuláris biológusok modellezik majd az élelmiszerek összetételét, az élelmiszergyártók pedig a világ bármely táján letölthetik majd a recepteket a szabadon hozzáférhető online adatbázisokból.

Ehhez nem is fűznék többet hozzá. Nézzük a feladvány megoldását.

A feladatban szereplő Táp-O-Mata nevű cég azzal reklámozza magát, hogy kevesebb mint négy év alatt megtalálja az összes lehetséges étel közül azt, amit a legjobban kedvelsz. A cégnél az ételalapanyagok egy íz- és illatkombinációból állnak, ami összesen egymillióféle lehet. Ezek mindegyikét elő tudják állítani ezer különböző hőmérséklet- és textúrakombinációban. Így tehát összesen egymilliárd különböző alapanyagegység áll rendelkezésre, és ezekből állítják össze az ételkomponenseket, amikre úgy tekinthetünk, mint egy-egy falatra.

Megjegyzés: jelenleg egyébként 28 ezer különböző molekuláról tudunk, amelyek előfordulnak az ételeinkben, lásd a FooDB adatbázisát.

A feladat szerint a cég egy ételkomponensben legfeljebb 7 egymástól különböző elemi egységet (alapanyagot) használ, az ételek pedig legfeljebb 7 egymástól különböző ételkomponensből tevődnek össze. Két ételt akkor tekintünk különbözőnek, ha a komponenseik között van eltérés, a használt mennyiség lényegtelen. Hasonlóan, két komponenst akkor tekintünk különbözőnek, ha a felhasznált elemi egységek között van eltérés, a használt mennyiséget figyelmen kívül hagyjuk.

A feladat szerint azért használjuk a bűvös 7-es számot, mert feltételezzük, hogy a munkamemóriával analóg módon átlagosan ennyi érzetet tudunk egymástól megkülönböztetve egyszerre érzékelni. Nézzük ezek alapján hány különböző étel előállítása lehetséges összesen.

Először a lehetséges ételkomponensek számát számoljuk ki. Legyen N = 10⁹ a felhasználható alapanyagok (íz, illat, hőmérséklet és textúra egybevéve) száma. Egy ételkomponens állhat csak egyetlen alapanyagból is, de maximum hét lehet benne, így a lehetséges ételkomponensek száma:

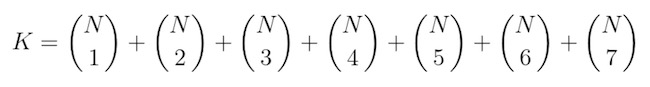
Itt a zárójel az ún. binomiális együtthatók felírásához használt jel. Az utolsó tagot például úgy olvassuk, hogy: N alatt a 7, és ez megadja, hogy N elemből hányféleképpen választhatunk ki 7-et. Mivel itt nagy számokról van szó, érdemes ezt a számítógépre bízni. A WolframAlpha ingyenes on-line felületén például az alábbit kell beírnunk, hogy kiszámolja nekünk:

K=bin(N,1)+bin(N,2)+bin(N,3)+bin(N,4)+bin(N,5)+bin(N,6)+bin(N,7), N=10^9

Ennek a végeredménye egy 60 jegyű szám:

K=198412695634920657142857073412698630753968326190476950000000

Ezek után a lehetséges ételek M számát hasonlóan számolhatjuk ki, csak most a K lehetséges ételkomponensből kell választanunk maximum 7-et:

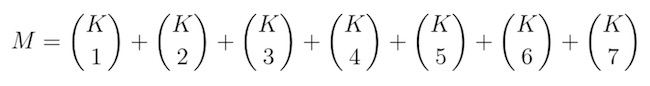
A WolframAlpha-nak ezt így érdemes beírni (és várni kicsit):

M=bin(K,1)+bin(K,2)+bin(K,3)+bin(K,4)+bin(K,5)+bin(K,6)+bin(K,7), K=198412695634920657142857073412698630753968326190476950000000

Az eredmény egy 412 jegyű szám, ami így néz ki, ha a jegyeit ötvenesével csoportosítjuk:

M =
24019041132098454465766321162455083021641751425343
38095330166507680301964276054313481888305729993133
82985071163449605135179556540828993375053171139779
75866889228892241209535154217266079982995640145585
80733170448494571404245470414572672946986180861395
26814611325257342489932790681363677288037147062745
83722216642360814892901123277759268169909633254233
48390583837748107068546682708729353922471318044993
481302500000

A feladat ezek után azt kérdezi, hogy ezt hány felezéssel lehet leszűkíteni valakinek a kedvenc ételére. Ehhez a kettes alapú logaritmusát kell venni M-nek, amire kb. 1366.6 adódik, ami azt jelenti, hogy nagyjából 3 év 9 hónapra van szükség a kedvenc étel kiválasztásához, ha naponta egy felezés történik. Ha mindezt a számolást 7 helyett 10-re játszuk végig a szuperízérzékenyek esetére, akkor több mint 7 és fél évre van szükség.

Kapcsolódó cikk a Qubiten:

link Forrás