Ész Ventura: A Qubit rést ütött a síkon!

Nem résmentes parkettázás című feladványunkban úgy kellett a síkot egységnégyzetekkel átfedésmentesen parkettázni, hogy azok majdnem az egész síkot kitöltsék, de a kimaradó rések a qubit betűinek alakját vegyék fel. Kikötés volt még, hogy a betűk vastagsága ne legyen egész szám. Az alábbiakban Boros Péter megoldónk megoldásaiból szemezünk.
A bemelegítő feladat az volt, hogy a q betűt hagyjuk ki a síkból, de a qubit összes betűjére van megoldás. Az alábbiakban a betű alakú rések körüli parkettázást mutatjuk csak, a parkettázás értelemszerűen folytatható minden irányban úgy, hogy kitöltsük a teljes síkot egységnégyzetekkel.
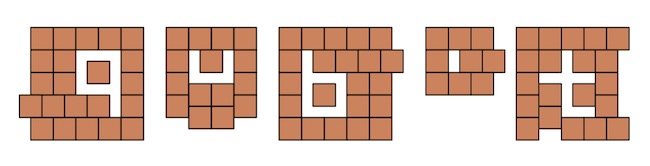
Az alapfeladványban a q és b betűket közösen kellett kihagyni. Lehetséges olyan konstrukció, hogy egy egész oldalhosszakkal rendelkező téglalapot úgy töltünk ki egységnégyzetekkel, hogy a téglalapon belül kimarad egy q és b betű alakú rés is, lásd a világosabb 5×7-es téglalapot az alábbi ábrán. Ha a téglalapon kívüli részt ezek után tömören töltjük ki, akkor az megoldás lesz az eredeti feladványra, de ha a mintázatot ismételjük, akkor végtelen sok q és b betűt is ki tudunk hagyni rácsba rendezetten, ahogy az ábrán is látható.

Egyébként a qubit betűit különféle párokban is ki tudjuk hagyni, lásd alább.
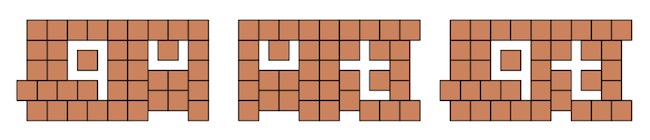
Sőt kihagyhatjuk csak a mássalhangzókat, vagy el is tudunk forgatni betűket, lásd például a szárára döntött b betűt a q betű mellett.
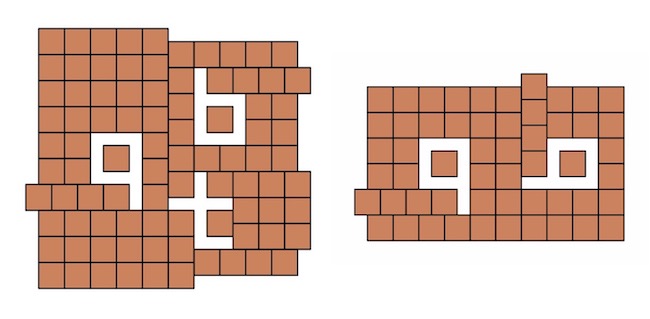
És a qubit összes betűjét is ki tudjuk hagyni egyszerre, sőt még a sorrend is az olvasásnak megfelelő lehet, lásd alább.
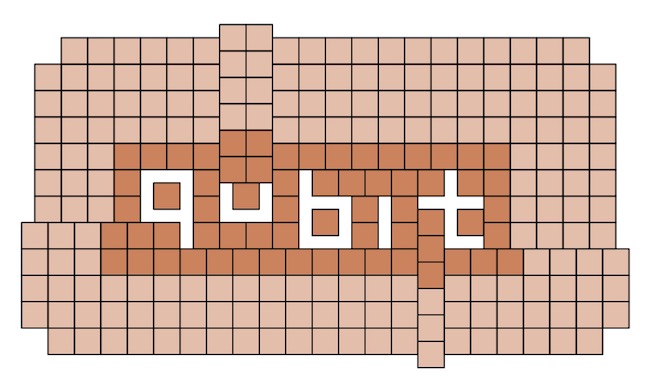
Aztán arra is van lehetőség, hogy egy-egy betűt akár végtelen sokszor kihagyjunk, nemcsak egy sorban, hanem akár a sík minden irányába végtelenül.
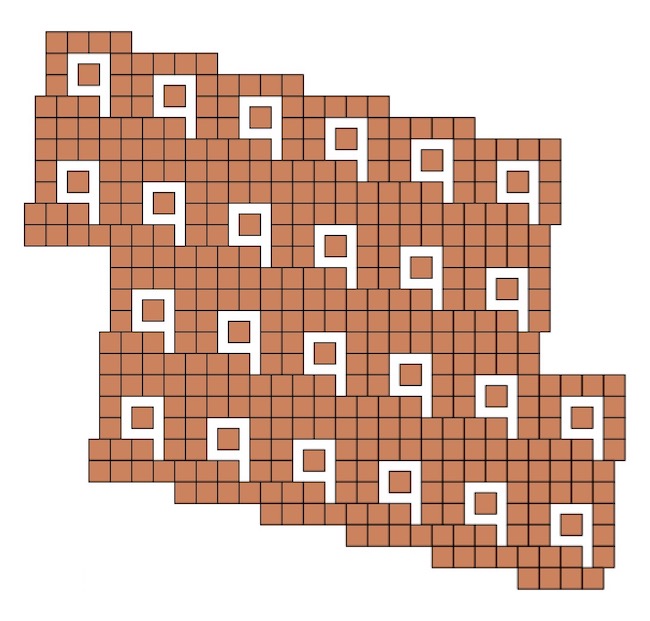
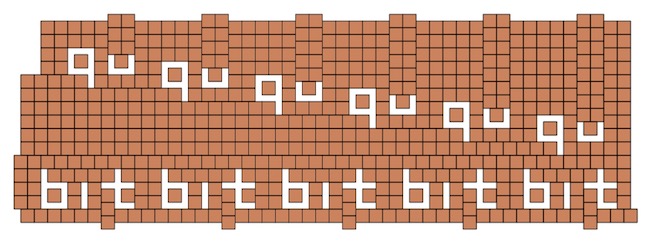
Emellett a qubit szó betűit is ki tudjuk hagyni végtelen sokszor, lásd például az alábbi konstrukciót.
Kapcsolódó cikk a Qubiten:
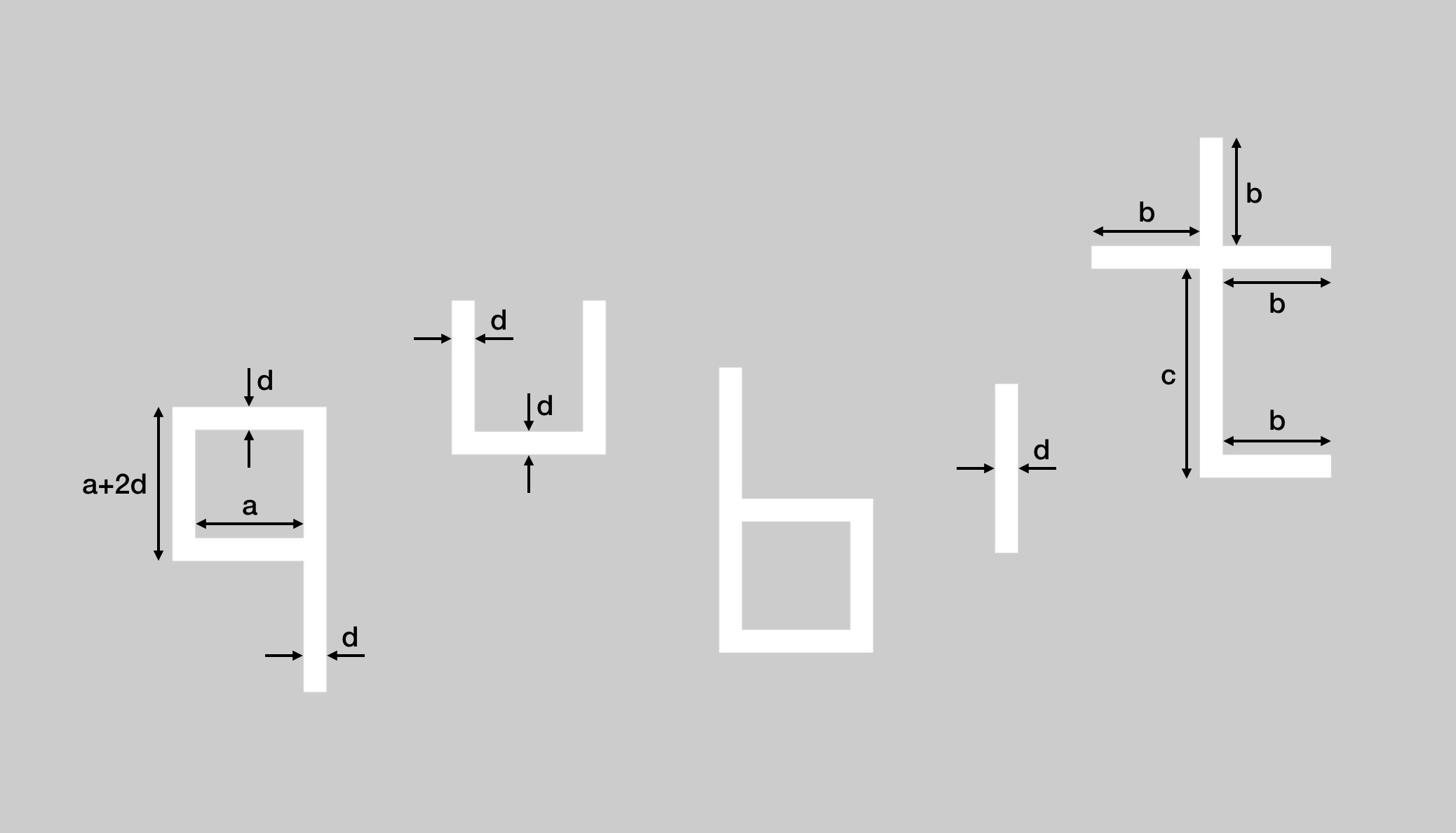
Ész Ventura: Csempézd ki a Qubitet!
Ki tudod csempézni a síkot átfedésmentesen végtelen sok négyzet alakú, egység oldalú csempével úgy, hogy a Qubit betűi kimaradjanak egységnél vékonyabb vonalakkal?