Érintkező gömbhéjdarabok című feladványunkban az volt a kérdés, hogy maximum hány olyan felületdarabot lehet megadni a gömb felszínén, amelyek egymással teljesen egybevágóak, nem fedik át egymást, de mindegyik érinti az összes többit, mégpedig nemcsak különálló pontokban, hanem görbeszakasz mentén.

Aki a Kuratowski-tétel alapján tudta, hogy az öt csúcsú teljes gráf (öt csúcs és az összes köztük menő él, lásd az alábbi ábrán) nem rajzolható le a síkba anélkül, hogy az élek egymást metszenék, az rögtön tudhatta, hogy öt felületdarabot hiába is keres a gömb felszínén a fenti feltételekkel, mert nem fog találni. De hogy jönnek ide a gráfok és a síkba rajzolhatóság, amikor a feladatban szó sem volt gráfokról, és a szóban forgó felület sem sík, hanem gömb?

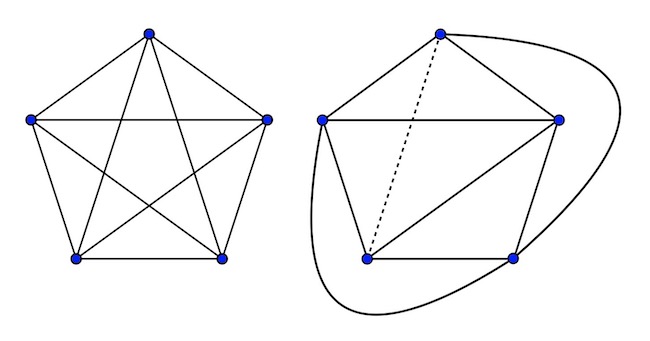
Hát úgy, hogy tegyük fel, hogy létezik a feladat feltételeinek megfelelő öt felületdarab a gömb felszínén. Válasszuk ki mind az öt felületdarabnak egy-egy belső pontját, legyenek ezek egy gráf csúcsai. A feladat feltételei szerint bármely két felületdarab vonal mentén érintkezik, ezért bármely két csúcsot össze tudjuk kötni egy vonallal (ezek lesznek a gráfunk élei) úgy, hogy az összekötő vonal csak a két szóban forgó tartomány belsejében haladjon és a közös határvonaluk belső pontján menjen keresztül. Egy adott tartomány belső pontjából pedig a határon lévő pontokba mindig tudjuk úgy húzni a vonalakat, hogy azok a tartományon belül ne messék egymást. Mindezek alapján tehát, ha létezne konstrukció öt tartománnyal, akkor az azt jelentené, hogy a gömbre tudjuk rajzolni az ötcsúcsú teljes gráfot anélkül, hogy a gráf élei metszenék egymást.

Már most ha a gömbre tudnánk rajzolni, akkor a síkra is, hiszen képzeljük el, hogy egy gömb alakú lufira rajzoltuk, majd kiválasztjuk a lufinak egy olyan pontját vagy kis tartományát, ahol éppen nincsen rajz, majd ott kilyukasztjuk a lufit, és kiterítjük a síkba. Mivel a lufi gumiból van, ezért szépen ki tudjuk síkká feszíteni úgy, hogy mindenhol feszes legyen, és ne legyenek benne ráncok. És bár torzulni fog minden vonal, de minden folytonosan fog változni, és ha eddig nem metszették egymást az élek, akkor a kifeszített ábrán se fogják metszeni. Viszont a Kuratowski-tétel kimondja, hogy az öt csúcsú teljes gráf nem rajzolható a síkba, tehát a kiindulási feltételünk nem teljesülhetett, vagyis nem lehetséges, hogy legyen a gömbön öt egymást páronként érintő felületdarab, függetlenül attól, hogy egybevágóak-e.

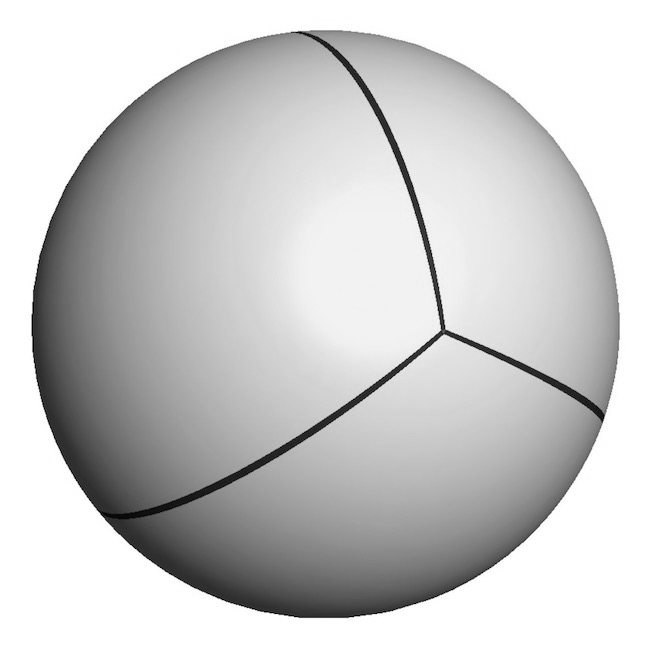
Négyet viszont könnyedén megadhatunk, elég ha elképzeljük, hogy a gömbünk egy szabályos tetraéder körülírt gömbje és a tetraéder lapjait a gömb középpontjából a gömb felszínére vetítjük. Az így kapott gömbhéjdarabok nem csak egybevágóak egymással és páronként érintik egymást, de hézagmentesen le is fedik a teljes gömböt.

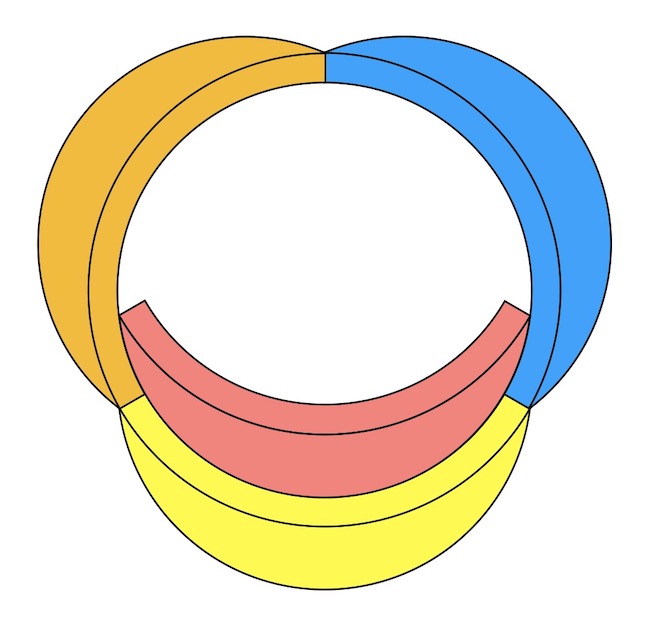
Bónusz kérdés volt, hogy mi a helyzet síkban? Ahogy láttuk, az öt csúcsú teljes gráf nem rajzolható a síkba, ezért öt tartományt a síkon sem tudunk megadni úgy, hogy páronként érintsék egymást vonal mentén. Négyre viszont számos konstrukció lehet, ahol a tartományok még egybevágóak is egymással. Dévai Gergely megoldása például az alábbi. Egy vékony körgyűrűt elharmadolunk, majd veszünk a harmadrészekkel egybevágó, negyedik alakzatot, amit betolunk a körgyűrű belsejébe, úgy, hogy a két sarka belülről érintse a szóban forgó gyűrűt. Ezután hozzávesszük a külső kör és a gyűrű belső köre által határolt sarlót is a negyedik alakzathoz, és ezt a sarlót az első háromra is „ránövesztjük” a körgyűrűn kívül.