82. feladványunkban az volt a kérdés, hogy egy négyzetet egy kétszer akkora csomagolópapírba akkor is be tudunk-e csomagolni, ha ferdén kezdünk neki.

A megoldást Dévai Gergely olvasónk megoldása alapján ismertetjük, aki egyedüli helyes megoldóként meg is nyerte a kisorsolásra szánt Pirueltt körzővel c. feladványos könyvet a Typotex Kiadó jóvoltából.

Vegyük a kis négyzet bármely P pontját, és tükrözzük a kis négyzetnek mind a négy oldalára. Ha az így kapott négy tükörpont (A, B, C, D) közül bármelyik beleesik a nagy négyzetbe, akkor a választott P pont lefedésre fog kerülni, ha a papírt a kis négyzet oldalai mentén behajtjuk.

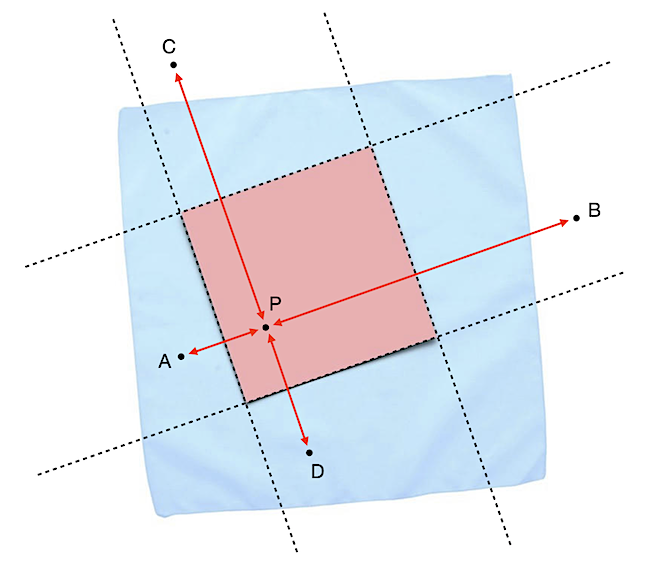
Be fogjuk bizonyítani, hogy nem lehetséges az, hogy mind a négy tükörpont a nagy négyzeten kívülre essék, vagyis a fenti módon a kis négyzet mindig becsomagolható. Tegyük fel, hogy van a kis négyzetnek olyan pozíciója és van olyan P pont, hogy a négy tükörpont mindegyike a nagy négyzeten kívül esik. Ha ebből ellentmondásra jutunk, akkor azzal bebizonyítjuk ennek lehetetlenségét, amit szeretnénk.

A tükörpontok közül a szemköztieket összekötve a kis négyzet oldalánál kétszer hosszabb, egymásra merőleges szakaszokat (AB és CD) kapunk, amik a P pontban metszik egymást. Ezen kívül az is igaz lesz, hogy az AC, CB, BD és DA szakaszok felezőpontjai éppen a kis négyzet csúcsai.

Legyen a kis négyzet oldala egységnyi. Feltevésünk szerint az AB és CD szakaszok metszéspontja (P) a nagy négyzetben van, de a végpontjaik azon kívül. Tehát mindkettő átmetszi a nagy négyzetet, vagyis mindkét szakasznak metszenie kell a nagy négyzet két különböző oldalát. Ezek az oldalak nem lehetnek egymással szemköztiek, mert ahhoz nem elég a szakaszok 2 egységnyi hosszúsága.

Ha az AB szakasz a nagy négyzet két szomszédos oldalát metszi, akkor a CD nem metszheti a másik két oldalát, mert akkor nem lehetne a két szakasznak a nagy négyzeten belül metszéspontja, hiszen az egyik szakasznak csak a négyzet egyik felében, a másiknak csak a másik felében lennének belső pontjai. Illusztrációként lásd a szaggatott átló mentén kettéválasztott négyzetet alább.

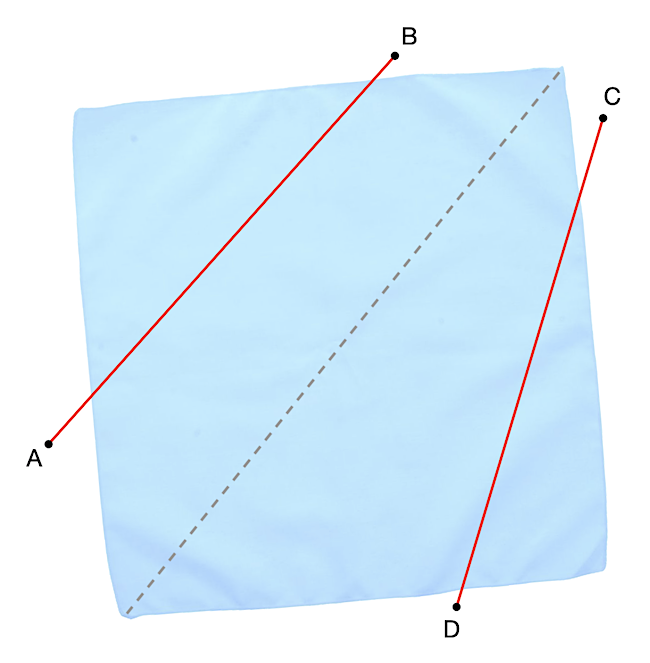
Azt kaptuk tehát, hogy biztosan van a nagy négyzetnek egy olyan oldala, amit az AB és a CD szakasz is metsz. Ha ezt az oldalt meghosszabbítjuk, akkor az a síkot két részre osztja, és mindkét szakasznak van egy-egy végpontja mindkét félsíkban. Legyenek A és C azok a végpontok, amelyek a nagy négyzetet nem tartalmazó félsíkba esnek. Korábban azonban megállapítottuk, hogy AC felezőpontja a kis négyzet egy csúcsa. Ez ellentmondás, hiszen AC-t úgy választottuk, hogy az teljes egészében a nagy négyzeten kívül fekszik, a kis négyzet viszont a csúcsaival együtt a nagy négyzetben van a feladat szerint.

Figyelem: különdíjért beküldhető még a válasz arra kérdésre, hogy mi a helyzet akkor, ha megengedjük, hogy a kis négyzet lelóghasson a papírról?

Kapcsolódó cikk a Qubiten: