Forgatgatós feladványunkban az volt a kérdés, hogy lehet-e úgy forgatni a négyzet alakú csempéket a helyükön, hogy vonalvégek sehol ne maradjanak szabadon az ábra belsejében. Tehát minden vonalnak záródnia kell, vagy az ábra szélére kell kifutnia.

A válasz az, hogy nem lehet, azaz nincs megoldás. Ahhoz, hogy ezt be is tudjuk bizonyítani, vegyünk észre, hogy kétféle csempe fordul elő az ábrán: egyenes vagy kanyar, és ezekre teljesülnek az alábbiak.

(1) Egyenes csempére mindig teljesül, akárhogy is forgatjuk, hogy a négyzet szemközti oldalain egyszerre fut ki vagy nem fut ki vonal. Ezen kívül, ha két egyes vonalat tartalmazó csempe egymás mellett van, akkor a vonalaik mindenképpen párhuzamosak egymással.

(2) Kanyart tartalmazó csempére mindig teljesül, akárhogy is forgatjuk, hogy szemközti oldalain ellentétes a vonal kifutása, vagyis abban az esetben, ha a csempe egyik oldalán kifut vonal, akkor biztosan tudhatjuk, hogy a szemközti oldalon nem fut ki vonal, és fordítva.

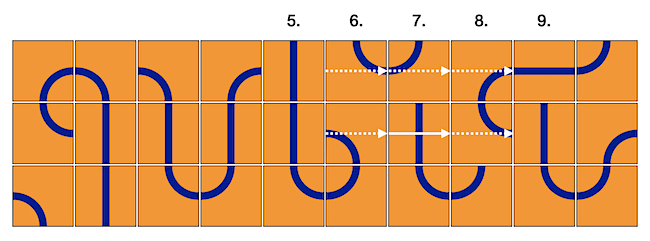
Nézzük most az 5. oszlopban lévő két felső csempét. Mindkettőn egyenes vonal van, és egymás mellettiek, ezért a vonal vagy mindkettőn függőleges (ahogy eredetileg), vagy mindkettőn vízszintes kell legyen. Tehát vagy mindkét csempéből megy jobbra vonal, vagy egyikből sem. Mellettük a 6. oszlopban két kanyar következik, ezek a szemközti oldalon (ahová a szaggatott nyilak mutatnak) ellentétesre változtatják a dolgot, vagyis ha jött be vonal (a nyilak kezdőpontjánál), akkor nem megy ki a másik oldalon, és ha nem jött be vonal, akkor megy ki a másik oldalon. Tehát a 6. oszlopban lévő fölső két csempére is igaz, hogy vagy mindkét csempéből megy jobbra vonal, vagy egyikből sem.

A 7. oszlopban azonban ez megváltozik, mert ott a felső két csempéből az egyik kanyar, a másik egyenes, az egyik vált, a másik nem. A szaggatott nyilak mutatják a váltásokat, a folytonos nyíl pedig azt jelzi, amikor nincs váltás, azaz a nyíl elején és végén is van belépő illetve kilépő vonal, vagy egyik helyen sincsen. Tehát azt kapjuk, hogy a 7. oszlopban lévő fölső két csempe esetében pontosan az egyikből mehet ki jobbra vonal: vagy a fölsőből megy jobbra vonal és az alsóból nem, vagy fordítva.

A 8. oszlopban két kanyar következik, mindkettő vált, ezért a 8. oszlopban lévő fölső két csempére is igaz az, ami a 7. oszlopban igaz volt, azaz pontosan az egyikből mehet ki jobbra vonal: ha a 7. oszlopban a fölsőből ment ki volna, akkor itt az alsóból fog, de a fölsőből nem, és fordítva.

Igen ám, de a 9. oszlop felső két csempéje egyenes vonalakat tartalmaz, vagyis abban az esetben, ha a fölsőbe jönne vonal balról, akkor az alsóba is kéne jöjjön, mert egyébként maradna vonalvég üresen. És hasonlóan, ha az alsóba megy vonal, akkor a felsőbe is kéne menjen, de ez ellentmondás, mert a 8. oszlopban lévő fölső két csempe közül, csak az egyikből érkezik vonal a korábbiak szerint.

Kapcsolódó cikk a Qubiten: