A kártyák egyik oldalán egy szám van, a másik oldaluk pedig színes. Hány kártyát és mely kártyákat kell megfordítani ahhoz, hogy ellenőrizzük az alábbi állítást?

Minden páros számot tartalmazó kártya hátoldala kék?

Ez az úgynevezett Wason-teszt vagy négykártya-probléma. Kutatások szerint a tesztet kitöltők mindössze tíz százaléka válaszol helyesen. Azonban sokkal nagyobb arányban adnak helyes választ az emberek, ha a kérdést hétköznapi kontextusba helyezik, például ellenőrizni kell, hogy egyik kiskorú sem ivott alkoholt, és a kártyák egyik oldalán italok vannak, a másik oldalán pedig életkorok.

A feladat helyes megoldása egyébként az, hogy a kettest és a piros hátlapú kártyát kell megfordítani. Sokan azt gondolják, hogy a kéket meg kell fordítani, pedig teljesen mindegy, hogy annak mi van a másik oldalán, mert ha történetesen nem páros szám lenne a másik oldalán, az sem sem cáfolná az állítást, a pirosat viszont meg kell fordítani, mert ha páros szám lenne a másik oldalon, akkor az cáfolná az állítást.

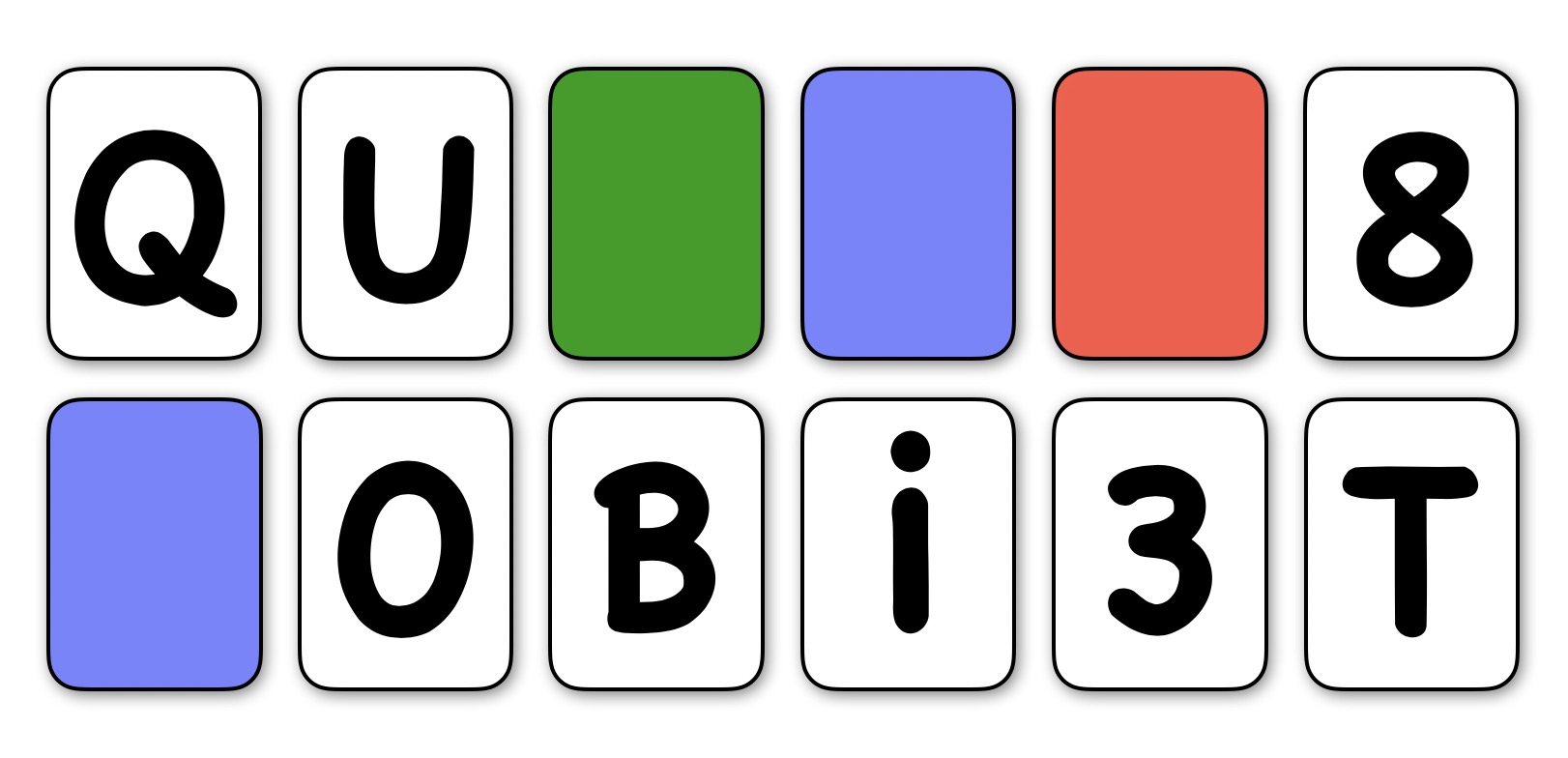
A Qubit-teszt című feladványunk a Wason-teszthez hasonló volt, csak kicsit bonyolítottunk rajta. Az volt a kérdés, hogy mely kártyákat kell megfordítani ahhoz, hogy ellenőrizzük azt, hogy az alábbi állítások egyszerre teljesülnek?

1. állítás: Minden páros számot tartalmazó kártya hátoldala kék.

2. állítás: Minden magánhangzót tartalmazó kártya hátoldala piros.

3. állítás: Minden zöld hátlapú kártya mellett közvetlenül (élszomszédosan) van egy betűt tartalmazó kártya.

Nézzük sorban, balról jobbra, fentről lefele, hogy mely kártyákat kell megfordítani.

• A Q betű nem páros szám, nem is magánhangzó, ezért az első két állítás szempontjából irreleváns, hogy milyen a hátoldala. A harmadik állítás szempontjából nézve meg kell vizsgálni azt is, amikor a Q hátlapja esetlegesen zöld, és az ő szomszédairól beszélünk, és azt is, amikor egy szomszédjának a hátlapja zöld. Mivel azonban a Q önmaga is betű, és van mellette is betű, nevezetesen az U betű, ezért ezen harmadik állítás miatt sem szükséges megfordítani; mindegy, hogy neki vagy a szomszédjának zöld hátlapja van-e.
• Az U magánhangzó, ezért ellenőrizni kell, hogy a hátlapja piros-e.
• A zöld lap se nem kék, se nem piros, ezért ellenőrizni kell, hogy a hátoldalán nem páros szám, illetve nem magánhangzó szerepel-e.
• A kék lap nem piros, ezért ellenőrizni kell, hogy a hátoldalán nem magánhangzó található-e.
• A piros lap nem kék, ezért ellenőrizni kell, hogy a hátoldalán nem páros szám található-e.
• A 8-as szám páros, ezért ellenőrizni kell, hogy a hátoldala piros-e.
  
• A bal alsó kék lap nem piros, ezért ellenőrizni kell, hogy a hátoldalán nem magánhangzó található-e.
• Az alsó sor második lapja értelmezhető O betűnek vagy 0-ás számnak, de mindkét esetben ellenőrizni kell, hogy a hátoldal milyen színű (az első esetben azt, hogy piros-e, a második esetben azt, hogy kék-e).
• A B betű a Q-hoz hasonlóan nem páros szám, nem is magánhangzó, és van mellette betűkártya, ezért nem kell megfordítani.
• Az i betű magánhangzó, ezért ellenőrizni kell, hogy a hátlapja piros-e.
• A 3-as szám nem páros, nem magánhangzó, az első két állítás szempontjából tehát irreleváns, hogy milyen a hátoldala. Ha a 3-as hátoldala zöld lenne, mivel van mellette betű, ezért emiatt sem kéne megfordítani. Ha egy szomszédja zöld lenne, akkor szintén lényegtelen, hogy megfordítjuk-e, hiszen látjuk, hogy a 3-as nem betű.
• Végül az utolsó kártya, azaz a T betű, nem is páros, se nem magánhangzó, viszont nincs mellette betű, ezért ellenőrizni kell, hogy nem zöld-e.

A fentiek szerint tehát 9 kártyát kell megfordítani, csak a Q, B betűket és a 3-as számkártyát nem.

A négykártya-probléma, vagy például a korábban kitűzött 101. feladványunk, tipikusan olyan egyszerű probléma, amely különbözik a szokásos IQ-tesztek feladataitól (IQ: intelligence quotient, azaz intelligenciahányados). Ha valaki már töltött ki IQ-tesztet, akkor emlékezhet rá, hogy ha az IQ-teszt egyik feladatáról azt gondoljuk, hogy megoldottuk, akkor valóban számíthatunk arra, hogy jó lesz a megoldásunk, csak az a lényeg, hogy milyen gyorsan jöttünk rá. A fenti négykártya-problémánál azonban a többség eljut egy látszólagos megoldáshoz, amiről tévesen azt hiszi, hogy jó megoldás. Az emberek nagy része nem képes ellenőrizni saját magát, és helyes logikával elemezni az összes lehetséges esetet.

Az IQ-teszt tehát más képességeket mér, mint amik a fenti feladatok megoldásához szükségesek, és ténylegesen ki is mutatható, hogy az IQ kevéssé befolyásolja azt, hogy ki tud egy ilyen típusú, racionális gondolkodást igénylő feladatot helyesen megoldani. Ebből az is következik, hogy aki intelligens, még nem feltétlenül tud helyes és racionális döntéseket hozni, ez pedig igen nagy probléma egyes befolyásos pénzügyi pozíciók esetében, sőt egyesek szerint hasonló okok miatt tört ki a 2008-as gazdasági világválság is, Nem csoda, hogy komoly pénzösszegeket áldoznak arra, hogy kidolgozzanak olyan úgynevezett RQ-teszteket (RQ: rationality quotient, magyarul racionalitási hányados) amik a racionális gondolkodás mérésére szolgálhatnak.

Az RQ-teszt kidolgozásának legnagyobb élharcosa Keith Stanovich, aki szerint az RQ-nak a kognitív elfogultság átlépésének képességét kell értékelnie. Az evolúció során kialakultak olyan intuitív mechanizmusok, amik segítenek komplex szituációk értékelésében anélkül, hogy tudatosítanánk a következtetéseinket, így a mindennapi életben nagyon gyakran a megérzéseinket használjuk – ezzel még a matematikusok is így vannak. Ez azonban azzal jár, hogy információkat torzítunk, és néha tévedünk. Az magas RQ-szint lényegében azt jelenti, hogy az illető ismeri saját tudásának határait.

Kapcsolódó cikk a Qubiten:

link Forrás