A Dobble hihetetlenül népszerű gyorsasági játék, Angliában pár év alatt több mint egymillió eladott példánnyal 2018-ra a legnépszerűbb kártyajáték lett, és mára rengeteg variációja megjelent a Bogyó és Babócástól a Harry Potteresig. Az eredeti Dobble fémdobozában 55 kerek lapot találunk. Ezek mindegyikén nyolc szimbólum van, mégpedig úgy, hogy bármely két lap szimbólumai között pontosan egy közös szimbólumot találunk – ezt kell minél gyorsabban megtalálni és bemondani a játékban, amikor kiteszünk két lapot színével fölfelé.

A kártyajáték mögött érdekes matematikai rendszer áll, aminek létezése annak köszönhető, hogy létezik hetedrendű véges projektív sík, ami önmagában sem magától értetődő. A Dobble-paklit lényegében tekinthetjük egy véges projektív geometriai rendszer reprezentációjának. Gondoljunk arra, hogy minden kártya egy pont, és minden szimbólum egy egyenes. Ha így tekintünk rá, akkor az, hogy bármely két kártya között van közös szimbólum, annak felel meg, hogy bármely két pont között megy pontosan egy egyenes. Ugye ismerős?

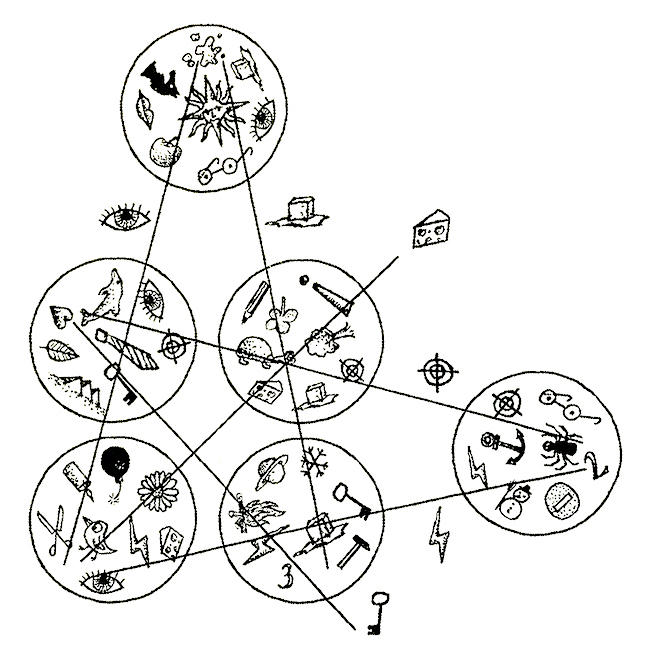
De nézhetjük fordítva is: legyenek a kártyák egyenesek és a szimbólumok pontok – ebben az esetben bármely két egyenesnek kellene legyen közös pontja. Na de álljunk csak meg egy pillanatra! Azt tanultuk, hogy a párhuzamosok sosem metszik egymást. A hagyományos síkon valóban nem, de ha bevezetjük a végtelen távoli ideális pontokat, megkapjuk az úgynevezett projektív síkot, ahol már bármely két egyenesnek pontosan egy közös pontja van, és az egyenesek és pontok teljesen szimmetrikusan viselkednek, egyfajta duális rendszert alkotnak.

A matematikusok számára a projektív sík nagyon hasznos, a hagyományos geometriát is azon szokták művelni, mert az említett dualitás miatt, ha bebizonyítanak egy tételt, akkor annak a duálisa is azonnal érvényes, amiben a pontokat és egyeneseket (a szavakat) csak kicseréljük egymással. Mármost láthatjuk, hogy a projektív sík a Dobble játék megalkotásához is nagyon hasznos, ha ugyanis ilyen projektív síkból létezik véges (amiben a pontok és egyenesek száma véges), akkor a pontokat és egyeneseket a fentiek szerint kártyáknak és a rájuk rajzolt szimbólumoknak megfeleltetve máris kapunk egy olyan kártyapaklit, amiben bármely két lap között van közös szimbólum, a duális tulajdonság pedig biztosít egyfajta homogenitási feltételt, amivel kezelhető lesz a kártyák és objektumok száma, mert ha például minden kártyán szerepelne minden objektum, az megoldás lenne ugyan, de se nem lenne túl érdekes, se nem túl praktikus.

Dobble a köbön című feladványunkban a Dobble általánosítását tűztük ki, amiben kártyapárok helyett kártyatriók között kell közös objektumot találni. A feladat tehát az, hogy tervezzünk olyan paklit, hogy a pakli bármely három lapján legyen pontosan egy közös szimbólum az ábrák közt. Ezen kívül megköveteljük az alábbi homogenitási követelményeket is, amik a Dobble esetében is teljesülnek: legyen minden kártyán ugyanannyi szimbólum, a kártyákon semmi ne szerepeljen duplán, egyik szimbólum se szerepeljen az összes lapon, de ne is csak három lapon, és minden szimbólum ugyanannyi példányban legyen jelen az egész pakliban.

Hogyan álljunk neki Dobble a köbönt tervezni?

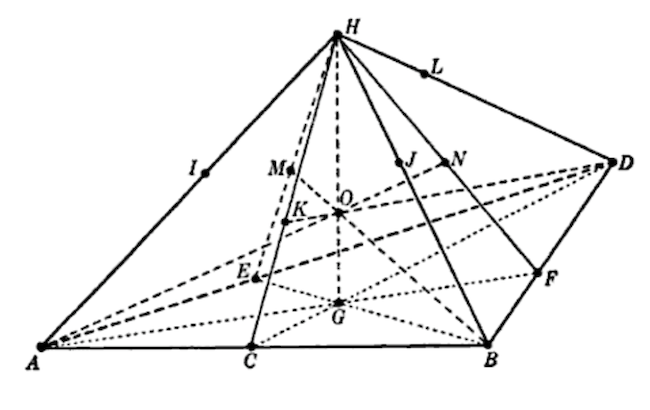
Az első gondolat az lehet, hogy ha a Dobble-hoz egy véges projektív sík kellett, akkor az általánosított Dobble a köbönhöz biztosan egy véges projektív teret érdemes keresni. Ha keresgélünk a neten, akkor hamar megtalálhatjuk a Wikipédián, hogy ebből a legkisebb a PG(3,2), aminek van egy szemléletes tetraéderes ábrázolása is, de hamar rájöhetünk arra is, hogy ez sajnos csak majdnem jó, de mégsem. Három tetszőleges pontra ugyanis nem igaz, hogy mindig egy és pontosan egy sík megy rajtuk keresztül, amikor ugyanis három pont egy egyenesre esik (kollineárisak), akkor több sík is keresztülmehet rajtuk.

A második gondolat az lehet, hogy akkor próbáljunk meg kézzel konstruálni egyet, lehetőleg a legkisebbet, azt talán sikerül megtalálni, ha létezik egyáltalán. Tegyük fel, hogy egy szimbólum M-szer szerepel a pakliban. Mivel a feladat szerint azt akarjuk, hogy 3-nál többször szerepeljen minden szimbólum, ezért M=4 a minimális, próbálkozzunk ezzel.

Ezen kívül gondolkozzunk el azon, hogy meg tudjuk-e könnyíteni esetleg a dolgunkat azzal, hogy valamilyen szimmetriát feltételezünk. Mivel homogén módon akarjuk elosztani a szimbólumokat, nagy könnyebbség lenne, ha 4 azonos szimbólumot 4 kártyára kiosztva rögtön a maradék kártyákra is tudnánk szimbólumokat osztani: így tartani tudnánk az egyensúlyt. A legegyszerűbb nyilván az lenne, ha 2M darab kártyából állna a pakli, és minden szimbólumnak lenne egy párja úgy, hogy minden lapon vagy az egyik, vagy a másik szerepelne komplementer módon, így a párok együtt pont lefednék az összes kártyát.

Ha ez lenne a helyzet, akkor nézzük meg, hogy ebben az esetben hányféle szimbólumra lenne szükség és hány szimbólum lenne egy kártyalapon. Mivel 8 lapból 56 féleképpen lehet kiválasztani tercet, és mivel egy szimbólum 4 példányban 4 tercet tud ezekből biztosítani, ezért 56/4 = 14 féle szimbólumra van szükségünk, és egy kártyán 56/8 = 7 szimbólumnak kellene lennie.

Ha most homogén módon elkezdjük a szimbólumpárokat kiosztani a kártyák között, hamar megtalálhatjuk kézzel az egyetlen lehetséges 8 kártyás megoldást. Két különböző párba tartozó szimbólum három kártyán nem szerepelhet együtt, mert akkor sértenénk az elvet, hogy bármely három kártya között pontosan egy közös szimbólum van. De csak egy kártyán sem szerepelhetnek együtt, mert akkor a másik párjával (komplementerével) három helyen fedne át. Tehát mindenképpen úgy kell kiosztanunk a szimbólumokat homogén módon, hogy két különböző párhoz tartozó szimbólum mindig pont két kártyalapon szerepeljen együtt. A megoldást a következő táblázat mutatja, amiben talán a rendszer is jól látható.

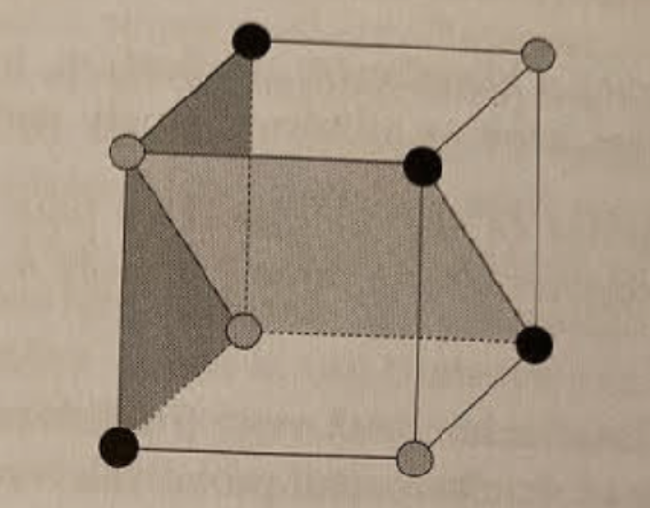
És most, hogy megvan a konstrukció, akár vissza is térhetünk a geometriához. Ez a nyolc kártya megfeleltethető a kocka nyolc csúcsának, és amit konstruáltunk, az az úgynevezett kockatér. Ebben az absztrakt térben a szimbólumok 14 absztrakt síknak felelnek meg, amik egyrészt a kocka sötétszürke lapjai (6 darab), plusz a világosszürke felező síkok (ugyancsak 6 darab), és még a feketével jelölt pontok által meghatározott halmaz és annak komplementere (még 2 darab), lásd az alábbi illusztráción:

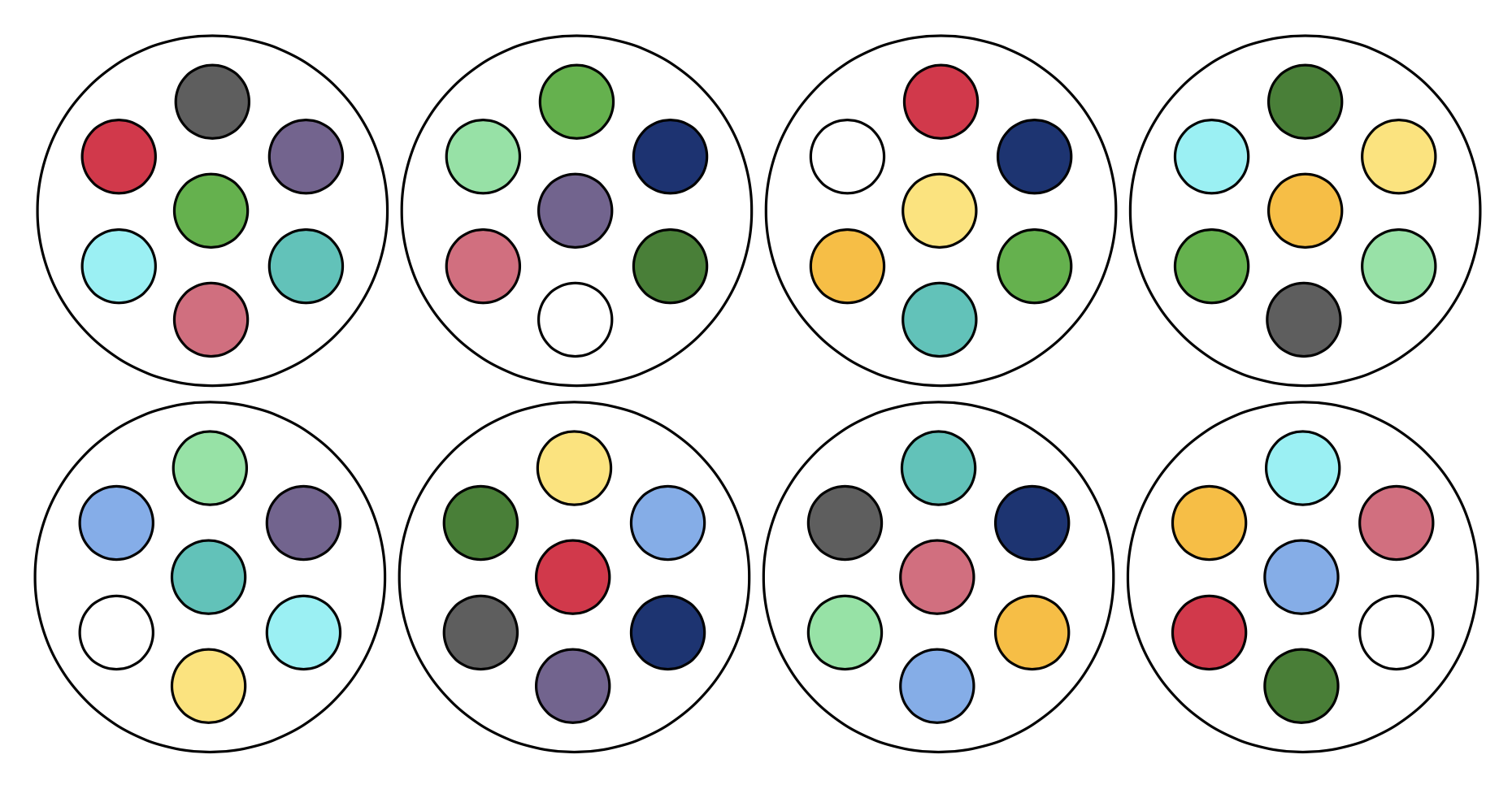
Ha ebből játékot akarunk csinálni, használhatunk például színeket, és akkor az alábbi módon nézhetnek ki a kártyáink:

De rajzolhatunk tetszőleges ábrákat is, ahogy egyik megoldónk, Szamoránsky János, tette karácsonyi hangulatban:

Kapcsolódó cikk a Qubiten: