117. feladványunkban 136 darab piros-kék érméből kiraktuk az ábrán látható 17×8 méretű, téglalap alakú rácsot úgy, hogy a qubit szó pirosan kirajzolódik benne. Megengedett lépés, hogy egyszerre átfordítsunk három közvetlenül egymás mellett lévő érmét egy sorban vagy egy oszlopban. A feladat az volt, hogy bebizonyítsuk: ilyen lépések sorozatával soha nem érhető el az, hogy minden érme kék oldala nézzen felfelé.

A bizonyítás könnyen megy, ha az érméket átlós vonalak mentén felválva három csoportba osztjuk, ahogy az alábbi ábrán is látható színekkel jelölve. Az egyes csoportokban rendre 45 (zöldek), 46 (rózsaszínek) és 45 (szürkék) érme lesz.

A játék kezdetekor a qubit szót kialakító érmék között 9 zöld, 8 rózsaszín és 7 szürke érme található, ahogy azt az alábbi ábrán láthatjuk. Nevezzük ezeket az érméket felfele néző érméknek. Mármost akár vízszintesen, akár függőlegesen fordítunk meg három közvetlenül egymás mellett lévő érmét, mindig minden csoportból pontosan egy érme fog fordulni. Bármelyik csoportot is tekintjük tehát, minden lépés során pontosan 1-gyel nő vagy 1-gyel csökken abban a csoportban a felfele néző érmék száma, vagyis paritást váltanak (páros után páratlan, páratlan után páros lesz).

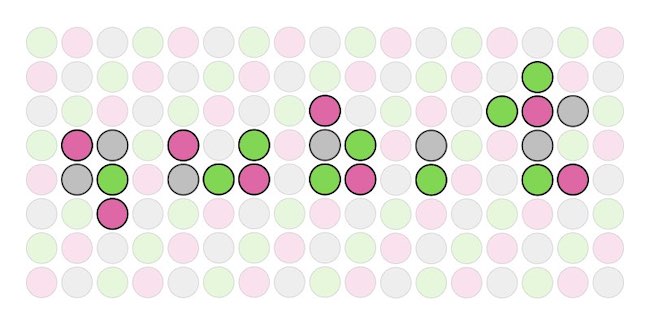
Mivel kezdetben eltérő paritású érme van felfordítva az egyes csoportokban (9, 8 és 7, ami két páratlan és egy páros szám), ezért ez a tulajdonság végig így is marad (következő lépésben két páros lenne és egy páratlan, majd újra egy páros és két páratlan). Tehát nem érhető el, hogy minden érme lefele nézzen, ahogy szeretnénk, mert abban a végső állapotban minden csoportban 0 érme nézne felfele, azaz a paritás egyforma (konkrétan páros) kéne legyen mindhárom csoportban, ami nem jöhet létre.

Kapcsolódó cikk a Qubiten: