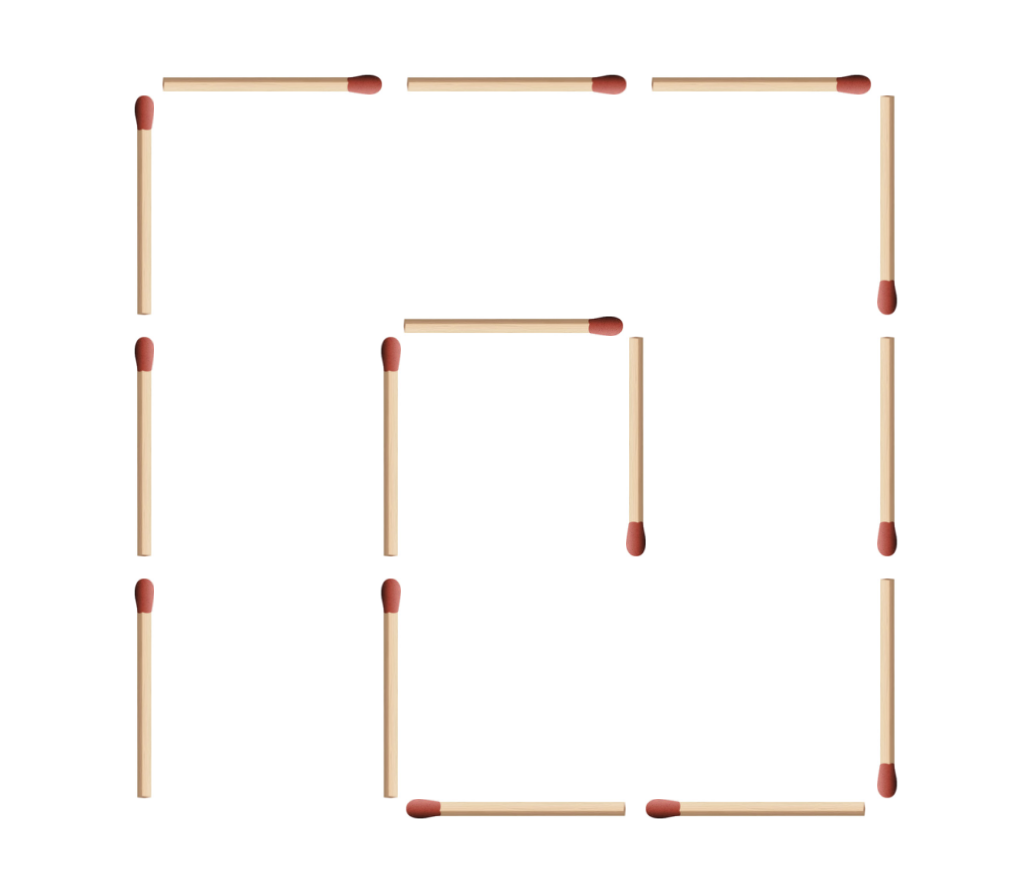
Ész Ventura: Az volt a kérdés, hogy egyetlen gyufaszál áthelyezésével hányféleképpen lehet szimmetrikus alakzattá alakítani a csigavonalat

Gyufacsiga című feladványunkban az volt a kérdés, hogy egyetlen gyufaszál áthelyezésével hányféleképpen lehet szimmetrikus alakzattá alakítani az alábbi gyufákból készült csigavonalat? A gyufafejek elhelyezkedésétől tekintsünk el a szimmetria megállapításakor.
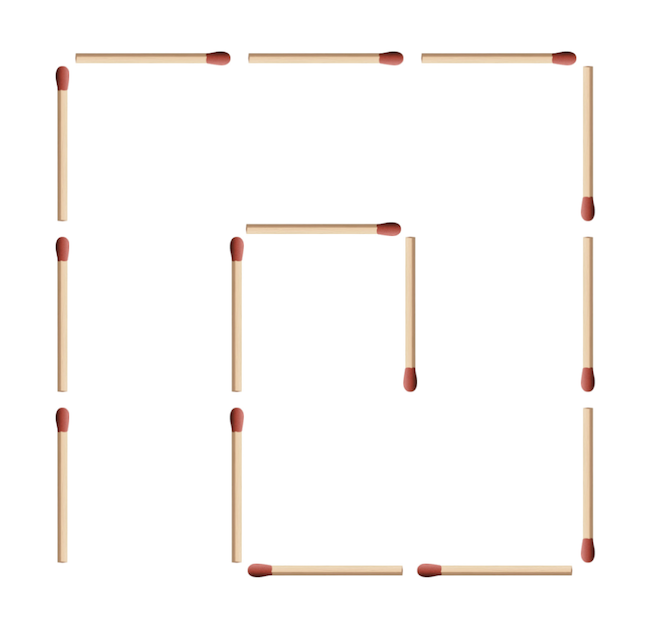
Az ábra külső kerülete nagy részben (sok gyufányi helyen) átfed egy négyzettel, és mivel csak egy gyufát mozgathatunk, ezért csak olyan szimmetriák jöhetnek szóba, amik ennek a négyzetnek is szimmetriái. A legtöbb megoldónk az oldalfelezőkre és átlókra vett tengelyes tükrözéseket és a középpontos tükrözést vette figyelembe, van azonban a négyzetnek még egy szimmetriája, a forgási szimmetria, azt is meg kellett volna vizsgálni.
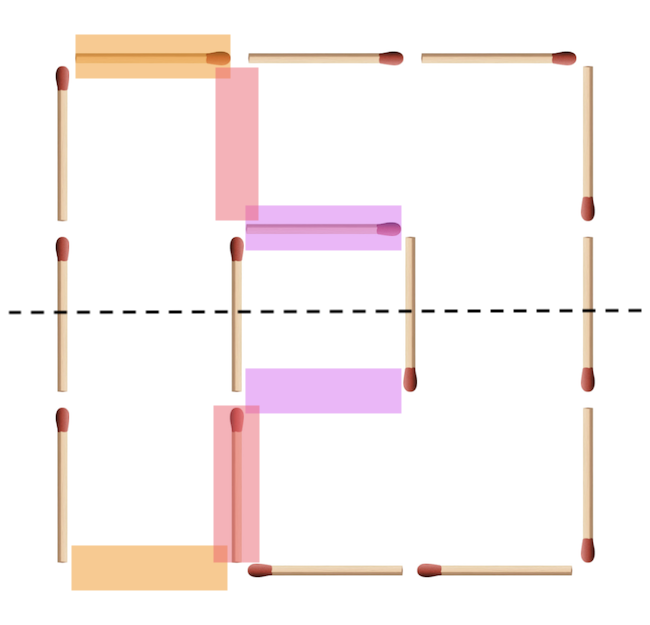
Érdemes úgy végigvenni a lehetséges szimmetriákat, hogy elképzeljük a tükrözött vagy forgatott ábrát, és összevetve a kiindulási ábrával, megnézzük, hogy mely gyufapozíciókban van eltérés. Nevezzük ezeket a helyeket szimmetriasértő helyeknek. A vízszintes tengelyre vett tükrözés esetében például az alábbi ábrán látható, hogy három pozíciópárban van szimmetriasértés, azaz különbség az eredeti és a tükrözött kép között, ezeket különböző színekkel meg is jelöltük.
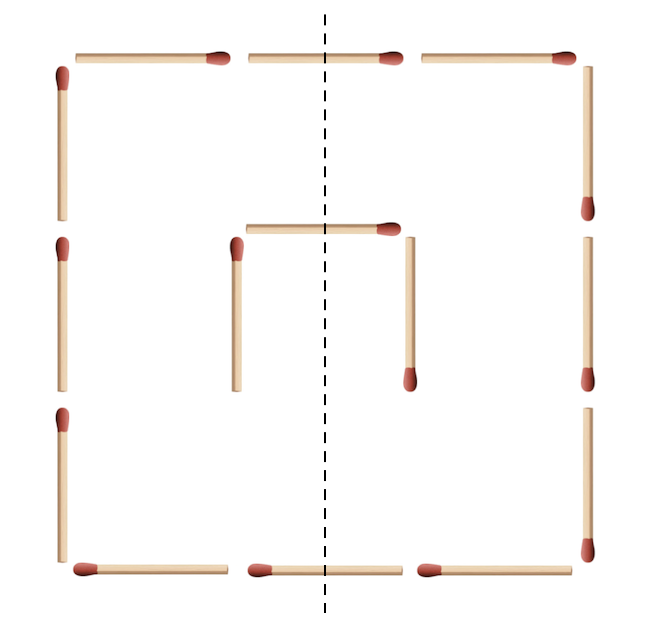
Mármost egy gyufa áthelyezésével legfeljebb két szimmetriasértés szüntethető meg, egy a gyufa régi pozíciójában, és egy a gyufa új pozíciójában. Ha végignézzük a korábban felsorolt összes szimmetriát ilyen módon, akkor kiderül, hogy csak a függőleges tengelyre való tükrözés esetén lesz lehetséges megoldás, ott azonban két megoldást is találunk, amiket az alábbi ábrák mutatnak.
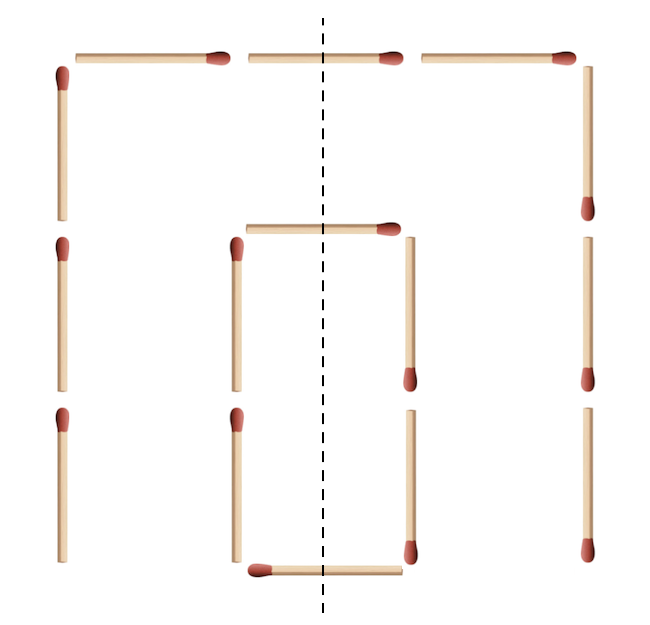
A legelső megoldó és a kreatív megoldásokért kiosztott banánok megtalálhatók a Dicsőségfalon!