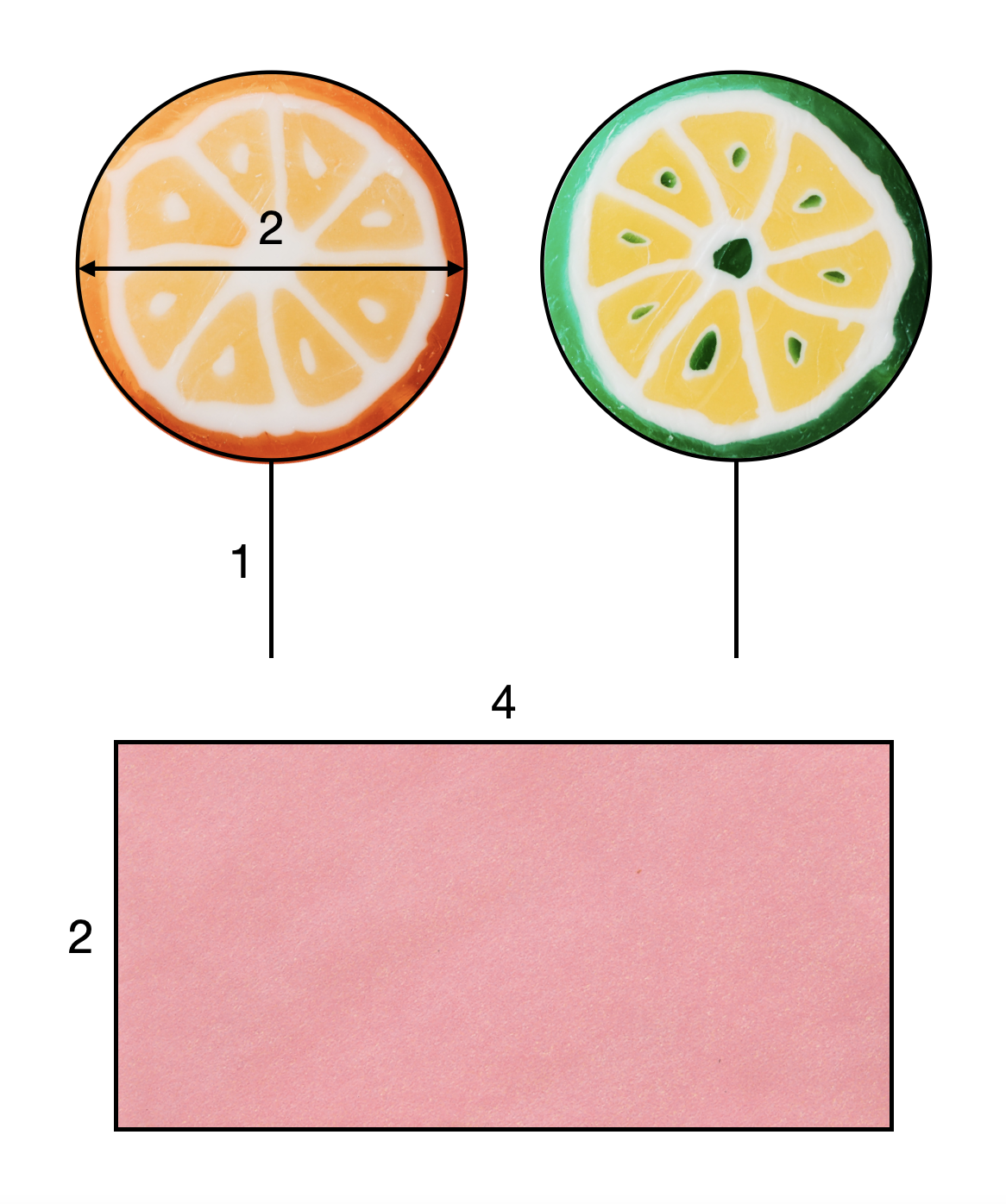
Két nyalóka című feladványunkban két egyforma kör alakú nyalókát kellett egy téglalapba csomagolni a szárukkal együtt. A szárak hossza pont a körök sugarával egyezett meg. A téglalap egyik oldalának hossza a kör átmérője volt, a másik pedig annak kétszerese. A nyalókák nem fedhetik egymást, legfeljebb érintkezhetnek egymással vagy a dobozzal. A nyalókák szárának vastagságától eltekinthetünk, de úgy kell elhelyezni őket, hogy a szárak sem metszhetik egymást.

Megmutatjuk, hogy a két nyalóka éppen befér a dobozba. A kör alakú részek elhelyezkedése egyértelmű, így csak a szárak helyzete a kérdéses. Fordítsuk úgy a nyalókákat, hogy száraik érintsék a másik nyalóka korongját, ahogy az alábbi ábrán is látszik: az egyik az egyik oldalon, a másik a másikon.

A két nyalóka korongjának középpontja és a Q érintkezési pont egy derékszögű háromszöget alkot, amelyet pirosra színeztünk az ábrán. A derékszög a Q pontnál van, hiszen a sugár merőleges az érintőre. Ezen piros háromszög átfogójának hossza két sugárnyi, rövidebb befogója pedig épp egy sugár. Az ilyen háromszögekről ismeretes, hogy hegyesszögeik 30 és 60 fokosak, de ezt az információt most nem fogjuk kihasználni.

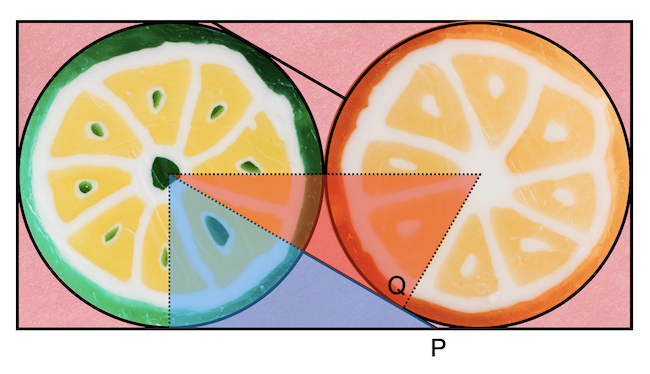
Az ábrán egy másik derékszögű háromszöget is megjelöltünk, amit kékre színeztünk. Ennél a derékszögű háromszögnél a derékszög a kör (citromsárga korong) és a téglalap érintkezési pontjában van, hosszabbik befogója pedig a téglalap (alul fekvő) oldalán fut egészen a P pontig. Most még nem tudjuk, hogy a P pont megegyezik-e a (citromsárga) nyalóka szárának végpontjával, a P pontról egyelőre csak annyit teszünk fel, hogy a nyalóka szárára fekvő egyenes metszéspontja a téglalap alsó oldalával.

A piros és a kék derékszögű háromszögek azonban hasonlóak egymáshoz, azaz a szögeik egyformák, hiszen kisebb hegyesszögeik váltószögek, mert a piros átfogója és a kék hosszabbik befogója párhuzamosak egymással. De nemcsak hasonló, hanem egybevágó is a két derékszögű háromszög, azaz méretük teljesen egyforma, hiszen a rövidebbik befogó mindkét esetben megegyezik egy kör sugarával. Ez esetben viszont a kék derékszögű háromszög átfogójának a hossza is két sugárnyi, vagyis a nyalóka szára, ami ennek épp a fele, a P pontig ér, tehát pont belefér a dobozba. Hasonlóan a másik oldalon is.

A legelső megoldó és a megoldásokért kiosztott banánok megtalálhatók a Dicsőségfalon!