Ész Ventura: Körbejártuk a körkörös problémát

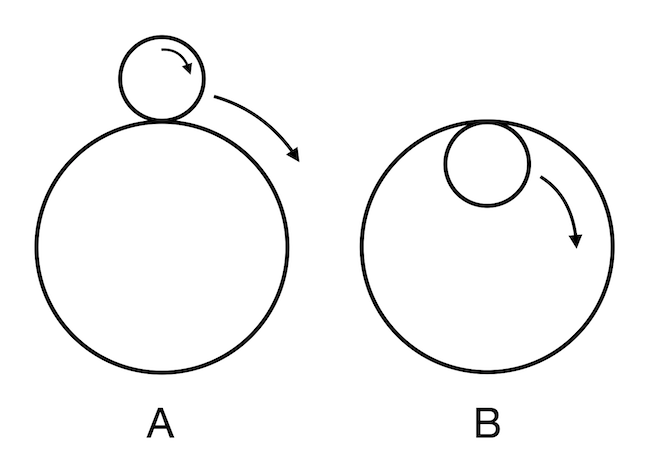
Kör körökön című feladványunkban egy régi feladatot jártunk körbe. Az eredeti feladat szerint van két kör, amelyek közül a kisebbik 1 egység sugarú, a nagyobbik pedig 3 egység sugarú. A kis kör csúszásmentesen végiggördül a nagy körön, lásd az alábbi illusztráción az A-val jelölt bal oldali ábrát. Hány fordulatot tesz meg a kis kör, míg visszaér eredeti pozíciójába a nagy körön?
A feladat 1982-ből egy amerikai érettséginek megfelelő vizsga (SAT teszt) feladatsorából származik. A hivatalos válasz 3 volt, de sok százezer diák közül néhányan jelezték, hogy a helyes válasz szerintük 4, ami nem is szerepelt a lehetséges válaszok között, és igazuk volt.
A feladat azért becsapós, mert a nagy kör kerülete épp háromszorosa a kis kör kerületének, tehát a gördülés során minden pontja valóban háromszor kerül érintkezésbe a nagy körrel. Eközben viszont a kis kör körbe is jár a nagy kör körül, és ez hozzáadódik a fordulatok számához, mert a gördülésből és a körbekerülésből származó szögelfordulások lényegében egymásra szuperponálódnak. Ez utóbbi tényleg számít: gondoljuk el azt, hogy a kis kör a nagy körön nem gördül, hanem, végig ugyanazon pontjával érintkezve a nagy körhöz, körbecsúszik. Nyilvánvaló, hogy ebben az esetben is tesz egy fordulatot, pedig nem is gördült semennyit. A legjobban ezt akkor láthatjuk és érthetjük meg, ha a kis kör szélén megjelölünk egy pontot, vagy ha a kis körre ráírunk valamit, és azt nézzük, hogy mikor lesz az írás újra az eredeti állásában – ezt szemlélteti ez a videó.
Ha a kis kör vízszintes egyenesen gördült volna a nagy kör kerületének megfelelő távolságon, akkor a válasz valóban 3 lett volna. Így viszont a helyes válasz 3+1 az A esetben, ha pedig a kis kör nem kívül, hanem a B ábrán látható módon a nagy a kör belsejében gördül végig, akkor a fordulatok száma 3-1 = 2 lesz, mert a gördülésből adódó forgás iránya az A esethez képest éppen ellentétes lesz. A haladás továbbra is az óramutató járásával egyező irányú, de a gördülés okozta forgás azzal ellentétes!
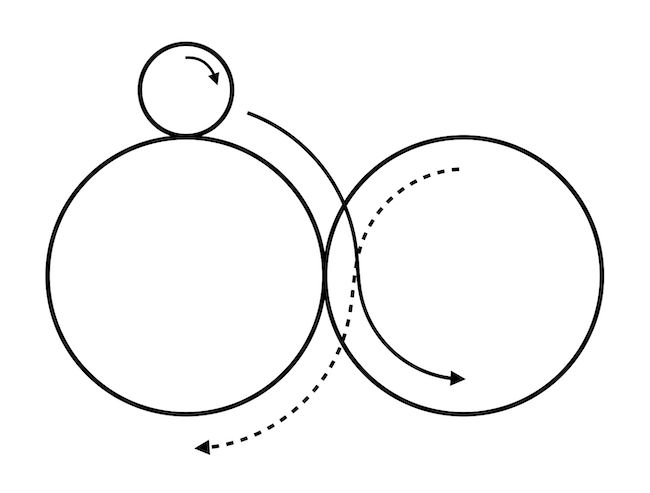
Volt még az általunk kitűzött feladványban egy olyan kérdés is, hogy hány fordulatot tesz meg a kis kör, ha a fenti ábrán látható két egymással érintkező nagy körön gördül végig egy fekvő nyolcas mentén úgy, hogy az egyik körnek a külsején gördül, a másiknak viszont a belsejében. A pálya önmetszésétől eltekinthettünk, arról feltettük, hogy nem akadályozza a mozgást.
Ebben az esetben azt láthatjuk, hogy összességében egy kört kívül fog megtenni a kis kör, egyet meg belül, tehát végeredményben 6 fordulatot fog megtenni.
A legelső megoldó és a megoldásokért kiosztott banánok megtalálhatók a Dicsőségfalon!
Kapcsolódó cikk a Qubiten:
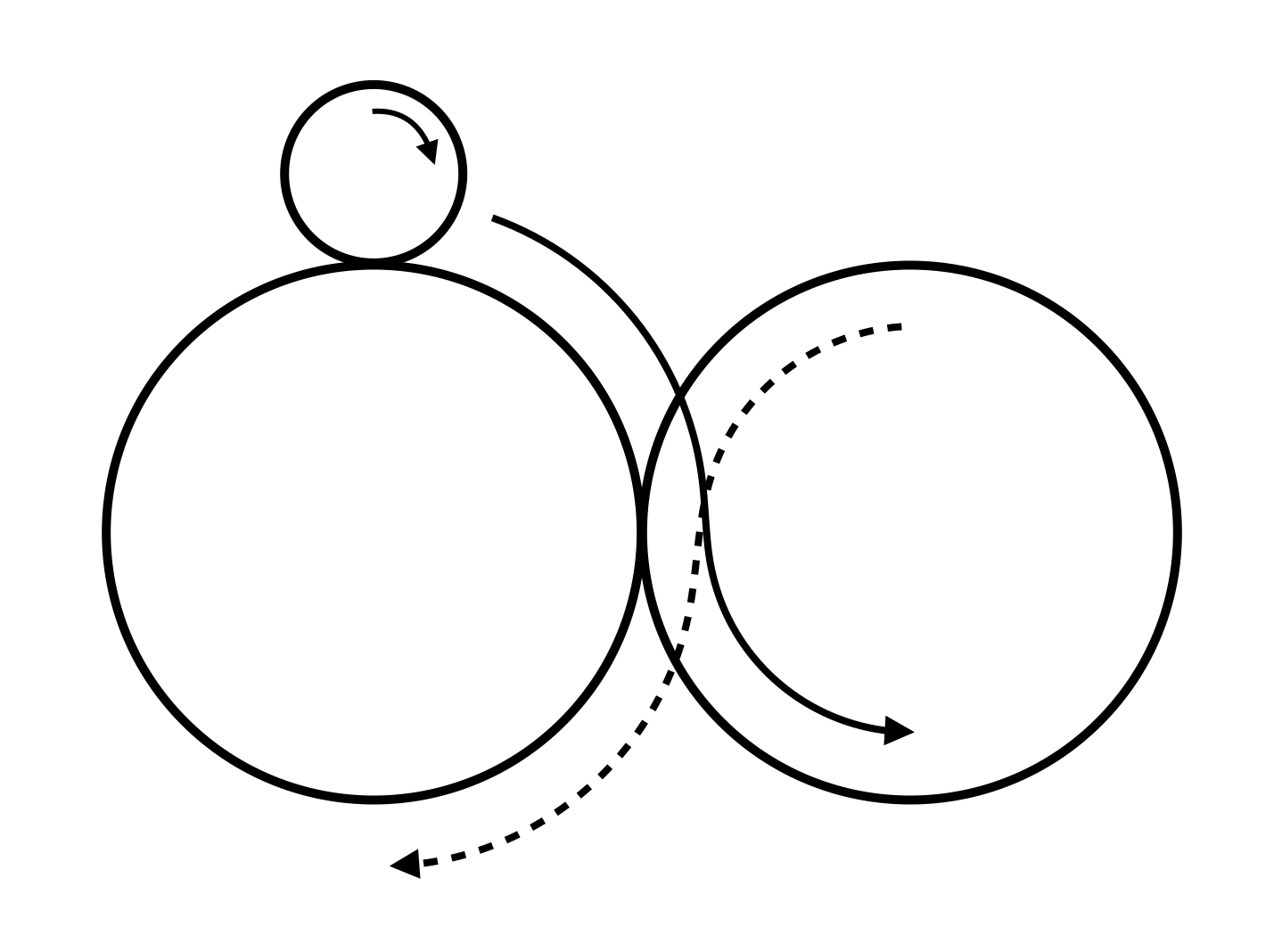
Ész Ventura: Okosabb vagy, mint egy amerikai gimnazista 1982-ből?
A kis kör harmadakkora, mint a nagy körök. Hányszor furdul körbe a kis kör, mire fektetett nyolcas mentén végiggördül az egymást érintő nagy körökön? Majd 40 éves amerikai érettségi szintű kérdés. Neked menni fog?