Egy olvasónknak köszönhetően a prímszámok rejtélyével bővült a tudományos mézeskalácsok gyűjteménye
Úgy fest, a tudomány karácsonykor nem csak minket ihletett meg. Egy olvasónknak köszönhetően tovább bővült a különleges mézeskalácsok gyűjteménye.
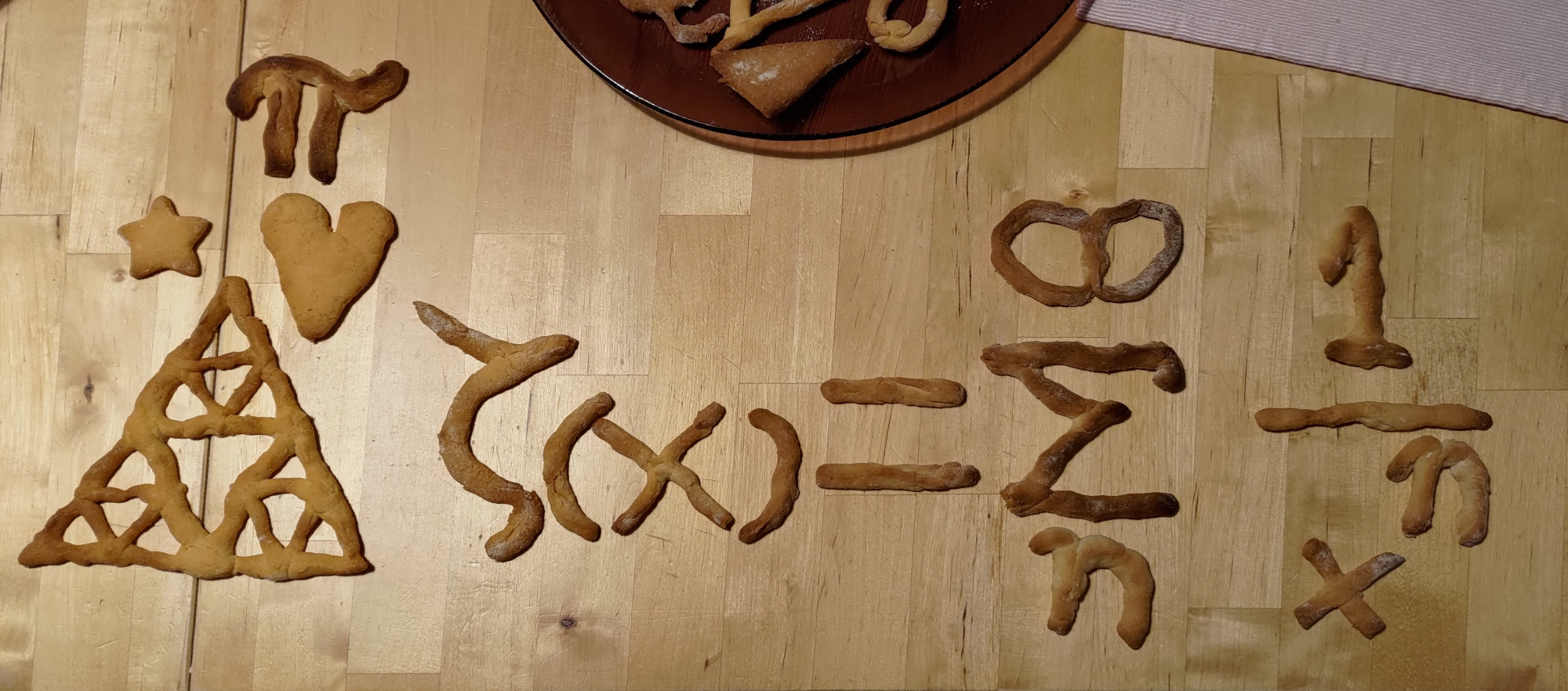
A Riemann-féle ζ(s) függvény konvergens sora süteményként sokkal barátságosabbnak tűnik, mint a négyzetrácsos papíron. Főleg, hogy a matematika egyik régi és máig megoldatlan problémájáról van szó. A Riemann-sejtés a prímszámok eloszlásával foglalkozik és összekapcsolja a komplex függvénytant a számelmélettel. Bizonyítása egyelőre nem ismert, bár a legtöbb matematikus igaznak fogadja el és vannak olyan matematikai elméletek is, amelyeket ráépülőként igazoltak.
Egy 2008-as interjúban Szemerédi Endre matematikus úgy fogalmazott, hogy ugyan a Riemann-sejtés is jól tartja magát, a megfejtésnek legtovább a Goldbach-sejtés állhat majd ellen. Utóbbi szintén a prímszámokkal foglalkozik, azonban nem az eloszlásukkal, hanem azzal, hogy összegük hogyan képez más összetett páros, illetve páratlan számokat.
A Riemann-sejtés megfejtése egyébként nemcsak parádés teljesítmény lenne, hanem egy 2004-es Guardian cikk szerint az internetes tranzakciók is sérülékenyebbé válnának. Ennek ellenére 2022-ben már közelebb vagyunk a megfejtéshez, mint valaha, a téma elismert szakértője, Yitang Zhang, a Kaliforniai Egyetem matematikusa novemberben a Riemann-sejtés analógjának megfejtésével állt elő.
Bár valószínűleg a karácsonyi asztalnál matematikai elméleteket nem igazolunk, további kreatív mézeskalácsokat még addig is készíthetünk. Ha más olvasóink is kedvet kaptak a sütögetéshez, örömmel látjuk további tudományos mézeskalácsaikat a szerk@qubit.hu e-mail címen.
Kapcsolódó cikkek a Qubiten:
