Ezen az alsó tagozatos matekpéldán vitatkozik a fél internet
Kivel ne fordult volna elő, hogy egy alapműveleteket tartalmazó matekpéldára a lehető legnagyobb magabiztossággal rávágta a rossz választ? Ez mindaddig nem olyan bosszantó, amíg ebből nem kerekedik egy fél világon átívelő vita, amelyben olyan emberek győzködik egymást, akik jó eséllyel soha nem is látták egymást. A közösségi oldalakon keringő, nagyjából az általános iskola alsó tagozatán tanultak alkalmazását megkívánó matematikai feladványok alatt többnyire vadidegen felnőtt emberek posztolják a saját eredményeiket, néhányan pedig napokon át győzködik magukat és egymást a saját igazukról.
Mi nemrég ebbe a matekpéldába futottunk bele, és még ha a közösségi oldalakon nem is, a szerkesztőségben azért kis híján ölre mentünk miatta:
A Twitter népe egy január 15-e óta keringő poszt alatt zajló vitában arra jutott, hogy az eredmény attól függően lehet 1 vagy 4, hogy a válaszoló melyik országban járt iskolába. Ez nem is csak az eredménynél, hanem már a feladvány értelmezésénél is komoly vihart kavart, néhány kommentelő ugyanis soha nem találkozott még azzal, hogy az osztást egymás feletti két pont (:) jelölte volna. Volt olyan is, aki szerint a válasz érettségiig 4, a matematikából felsőfokú tanulmányokat is folytatók körében viszont 1. A kommentfolyamban azonban felbukkan egy hasonló problémát Youtube-videóban elmagyarázó matematikus is, aki szerint az efféle virális példák azért nagyon bosszantók, mert a matematikai problémák sokszínűségének a valódi szépségét homályosítják el egy pontatlanul felírt művelet segítségével. Ő viszont nem árulta el, hogy szerinte mi az eredmény.
Saját kútfőből nem ment, szóltunk az MI-nek
A Qubit szerkesztőségében az 1 és a 4 három-három szavazatot kapott, pedig mindenki Magyarországon végezte az iskoláit, és senki nem matematikus. Miután hiába győzködtük egymást, a mesterséges intelligenciához fordultunk. A ChatGPT-t három próbálkozásra kétféle választ adott. A program 3.5-ös verziója szerint az eredmény 6, és ugyanerre jutott a Bing chat kiegyensúlyozott verziója is, amelyen a 4.0-ás ChatGPT fut.
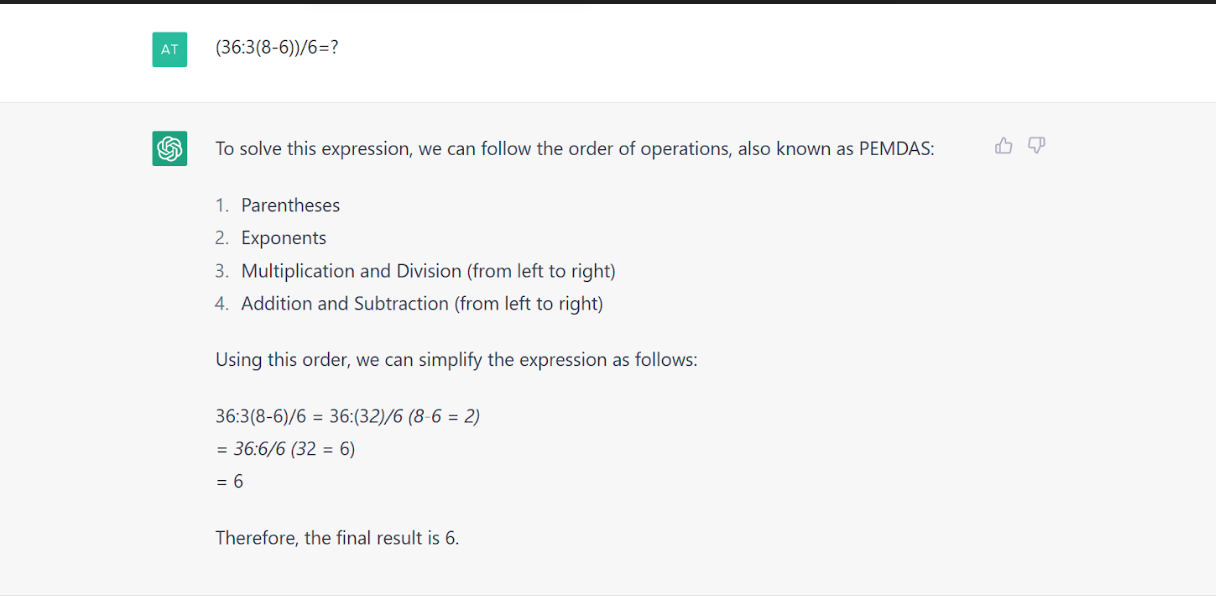
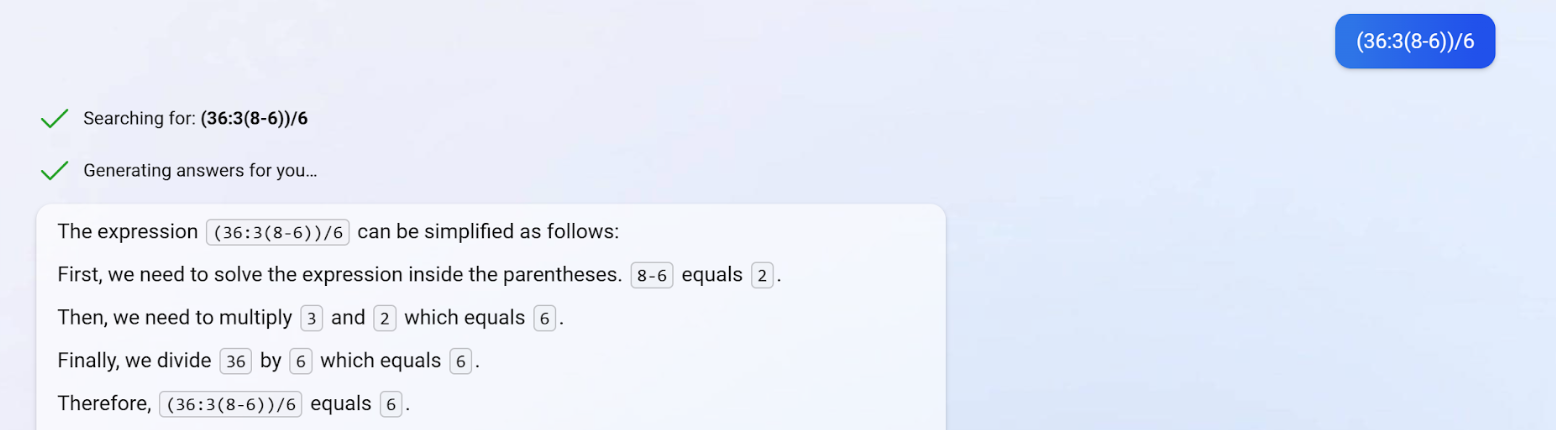
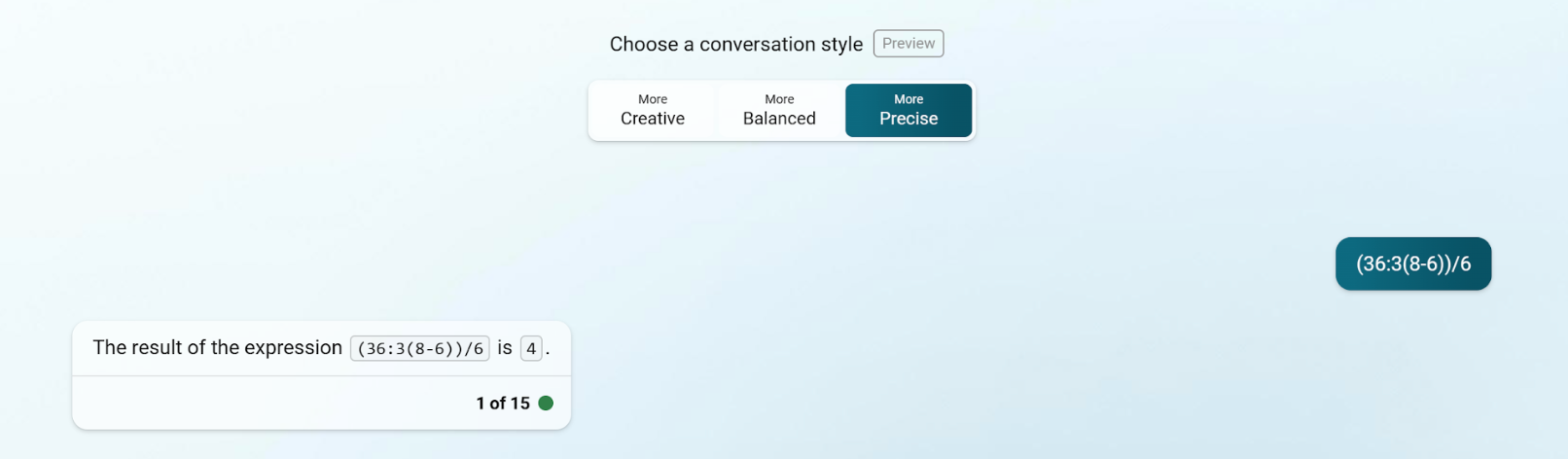
Precízre hangolt módban a Bing chat közelít a humán teljesítményhez: 4.
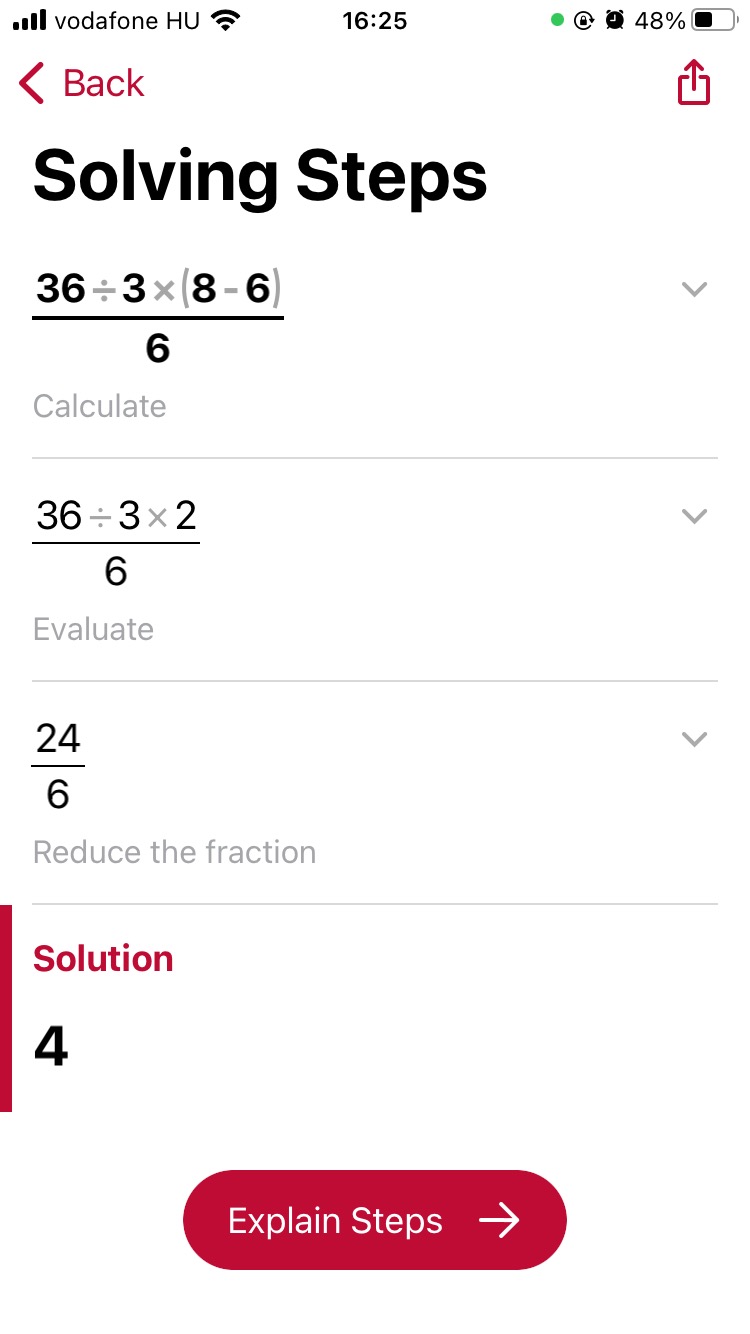
Beolvastattuk a feladványt a Photomath nevű ingyenes mobilalkalmazásba is, amely szerint szintén 4 az eredmény, viszont az algoritmus, miközben értelmezte a feladatot, egy helyen belenyúlt a képletbe, és csak azután számolta ki a feladványt.
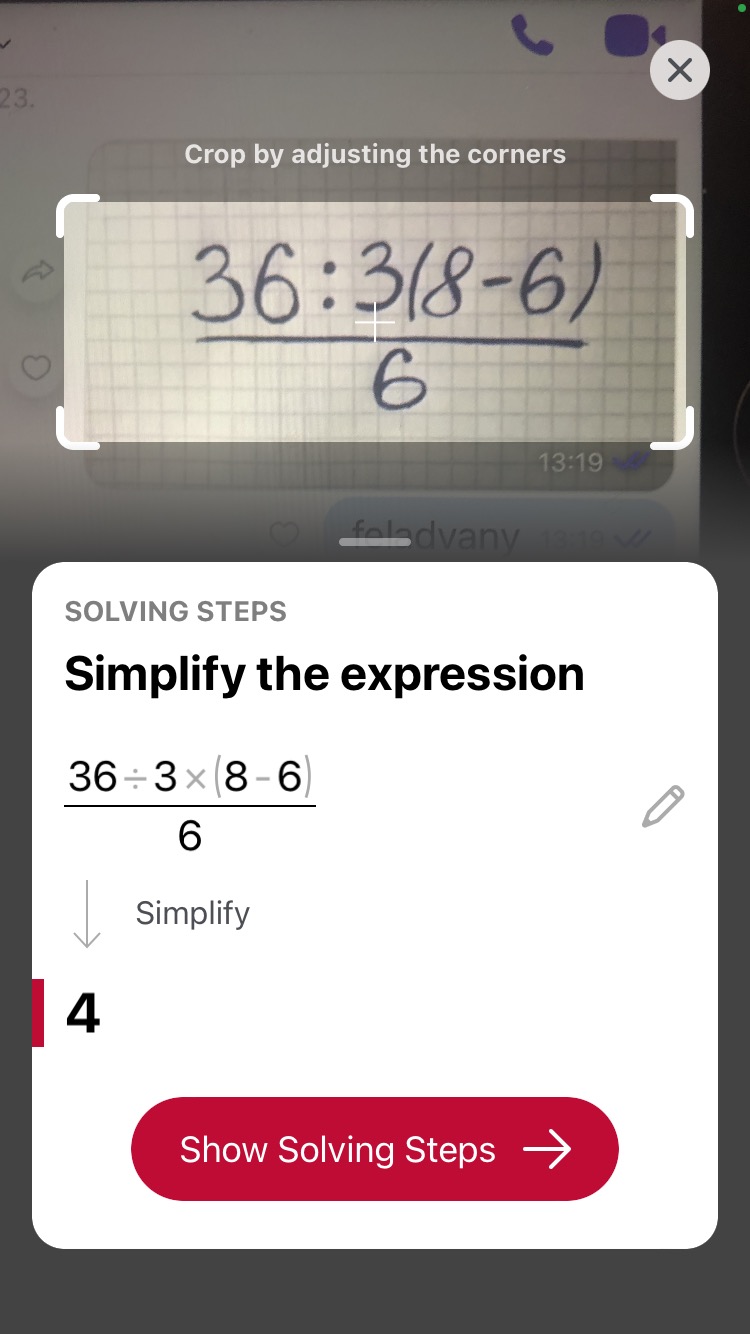
A 4-re szavazó kollégákat ez már-már meggyőzte, de az 1 hívői nem adták fel egykönnyen: megkérdeztünk néhány olyan szakembert, akik mindennapi munkájuk során így vagy úgy matematikával foglalkoznak.
- Tanulság #1: Ha netán rossz eredményt kapsz egy egyszerű matekpélda megoldásakor, ne add fel: keress egy matematikust, aki úgy fogja elmagyarázni, miért lehet mégis igazad, hogy a felét sem érted a levezetésnek.
- Tanulság #2: Az eredmény érettségiig mindenképpen 4, néhány egyetemi matekszigorlat után még mindig lehet 4, de valójában inkább 1.
Az általunk megkérdezett szakemberek megoldásai:
Csordás Valéria nyugdíjas általános iskolai matematika tanár: 4
„Először a zárójelben lévő műveletet kell elvégezni, majd a továbbiakban így alakul a feladvány: (36:3·2):6=(12·2):6=24:6=4”
Fazekas Benedek bölcsész végzettségű szenior programozó: 4
„Először a zárjójelet kell feloldani, amiből így lesz: (36:3(2))/6. Itt van egy kis beugratás mert a 3·2 az implicit, de szerintem ennek nem kell beugrani, a szorzás-osztásokat sorrendben, balról jobbra haladva kell elvégezni, vagyis ebből lesz (12·2)/6, ami 24/6, vagyis az eredmény 4.”
Neve elhallgatását kérő programozó matematikus: 4
„A műveletek prioritása és sorrendje a kulcs, a trükk csak annyi, hogy egyenlő prioritású műveleti sornál simán balról jobbra kell haladni, a törtnél meg számláló-nevező sorrendben, azt hiszem. Egyébként a ChatGPT mit mond?”
Kegyes Tamás matematikus, adattudós doktorandusz: 4
„A feladvány látszólagos nehézségét az adja, hogy a zárójel és a 3-mas szorzó közé nem írtak műveleti jelet, emiatt úgy tűnhet, mintha szorosabban összetartoznának, és azt a számlálóban a zárójel feloldása után a szorzást kellene az osztás előtt elvégezni. Ha pisztolyt tartanának a fejemhez, és csak egyetlen számot mondhatnék, azt mondanám, hogy a végeredmény 4, mert a szorzásjel elhagyása ellenére is úgy gondolnám, hogy az egyenrangú műveleteket balról jobbra kell elvégezni, vagyis a sorrend a következő: zárójel, majd osztás, szorzás, és újabb osztás. Akárcsak egy egyenletnél, ahol minden lehetséges egyszerűsítést visszamásolunk az eredeti feladványba: ((36:3(8-6))/6 = (36:3·2)/6 = (12·2)/6 = 24/6 = 4”
Gáspár Merse Előd, fizikus, blogger, a Qubit állandó szerzője: 4, de inkább mégis 1
Az, hogy én mit mondok, vagy hiszek nem nagyon számít, a szabály az érdekes. A szorzás és osztás azonos rendű művelet és ha nincs zárójelezve, akkor balról jobbra kell kiértékelni. Ezt a szabályt nagyon ritkán alkalmazzák, mert inkább egyértelműsítik zárójelekkel. Ha ez mégsem történik meg, akkor inkább azt feltételezi az ember, hogy aki írta, az sem vette észre, hogy kérdéseket vet fel (annak aki nem ismeri a balról jobbra szabályt), ráadásul, ha szabályosan számoljuk is ki, nem biztos, hogy aki írta, valóban arra gondolt, amit írt. Fizikusoktól eleve kár ilyesmit kérdezni, mert a tudományban ilyen képlet önmagában nem fordul elő, mindig van egy olyan szövegkörnyezet, amiből kiderül, hogy mit akar kifejezni.
„Szóval a kivonás az első a zárójelben: 8-6 = 2. Ezek után ami marad a számlálóban: 36:3·2, de a sorrend balról jobbra, tehát (36:3) 2 = 12·2 = 24, a végeredmény 24/6 = 4. DE: kérdés, hogy attól, hogy a szorzás jelét a zárójel előtt nem írtuk ki, elsőrendűbb lesz-e a példában szereplő szorzás, hiszen olyan, mintha összevonódna a zárójellel. Ezt implicit szorzásnak is szokás hívni. Ha kitehette volna a szorzás jelét, de nem tette ki, akkor az egyértelmű, mert egyébként zárójelezni kellett volna. Én emiatt az implicit szorzás elsőbbségét használnám, azaz 36:(3·2) = 6, és akkor 6/6 = 1.”
Csóka Endre matematikus, a Rényi Alfréd Matematikai Kutatóintézet kutatója, a Qubit állandó szerzője: 4, de inkább mégis 1
A kérdés lényege, hogy a számlálóban mi a műveletek sorrendje. Az egyértelmű, hogy először a 8 - 6 = 2-t végezzük el a zárójel miatt. Ha a szigorúan vett szabályokat nézzük, akkor az osztás és a szorzás azonos rendű műveletek, balról jobbra végezzük el: 36 : 3 = 12, és 12 · 2 = 24. Majd ezt osztjuk 6-tal, az eredmény 4.
Főleg bonyolultabb kifejezéseknél azonban előfordul, hogy nem tartjuk magunkat szigorúan ezekhez a szabályokhoz, hanem a könnyebb átláthatóság kedvéért egyes zárójeleket elhagyunk, ha az nem okoz félreértést. Például a
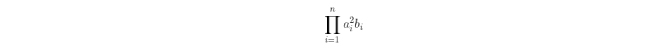
kifejezés a szigorúan vett szabályokat tekintve azt jelentené, hogy
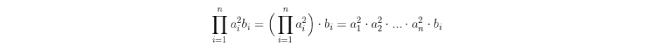
ami ráadásul nem is lenne szabályos és egyértelmű, mert azt jelentené, hogy az i-nek már van egy funkciója bᵢ-ben, majd mégis ugyanezt a betűt használtuk a produktumon belüli futó változónak. Ezért aki gyakran találkozik ilyen képletekkel, annak világos, hogy valójában ezt akarták kifejezni, megszegve a műveleti sorrendre vonatkozó szabályokat.
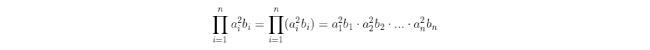
Ezt a gyakorlatban nem is tekintjük hibának, tudományos publikációkban is gyakran használjuk így.
„Visszatérve tehát az eredeti képletünk számlálójára, egyrészt látszik, hogy ki nem írt szorzást használtak, ami a tényezők közötti szorosabb összetartozásra utal. Másrészt osztásnak a „ : ” jelet használták, ráadásul előtte és utána némi helykihagyással, ami kifejezetten arra utal, hogy itt két mennyiség aránya van a számlálóban. Ezért ha azt látnám, hogy ez egy számolás részeredménye volt, akkor majdnem biztosra venném, hogy aki ezt leírta, az a 36 : (3(8-6))-ra gondolt, csak lefelejtett egy zárójelet. Vagyis az eredmény: 1
Hozzátenném azonban, hogy ezek a kérdések egyáltalán nem matematikai kérdések, hiszen a jelölésrendszerről szólnak. Kicsit olyan, mint egy irodalmi műben azt nézni, hogy a mondatok között mennyivel nagyobb a helykihagyás, mint a szavak között.”
Kapcsolódó cikkek a Qubiten: